9 клас Алгебра

 

(Дистанційне навчання)

 

 

                                                Вчитель математики

                                                Каплунівської гімназії

                                                Бабич Юлія Іванівна

 

20 листопада 2023 р.

9 клас Алгебра

Урок 20 (Дистанційне навчання за допомогою підручника “Алгебра, 9 клас (автор Істер О. С.), гаджета та онлайн дошки джамборд).

Тема. ФУНКЦІЯ у=ах²+bх+с, а≠0, ЇЇ ГРАФІК І ВЛАСТИВОСТІ

Мета. Сформувати знання учнів про означення, алгоритм побудови графіка квадратичної функції, вміння розв'язувати вправи.

Тип уроку. Урок формування знань і вмінь.

Хід уроку.

1.    Організаційний момент.

1.     Перевірка наявності учнів у класі, в наявних на платформі  Meet.
2.     Перевірка готовності учнів до уроку.
3.     Запис у зошитах дати уроку і теми.

2.    Перевірка домашнього завдання.

Усно: (демонстрація розв’язання домашньої роботи на екрані).

Пройти тест “Квадратична функція” (8 запитань) на онлайн-платформі “НаУрок”.

-      Графіком функції у = х² є…

-      Областю визначення функції називаються…

-      Областю значень функції називаються…

-     Нулями функції називають…

-     Найбільшим значенням функції називають…

-     Найменшим значенням функції називають…

 

ІІІ. Мотивація навчальної діяльності, повідомлення теми та мети уроку.

Тема нашого уроку «Функція у=ах²+bх+с, а≠0, її графік і властивості»

Вивчивши способи геометричних перетворень графіків функцій, можна побудувати графік будь-якої алгебраїчної функції. Математична компетентність є основою багатьох наук. Вміння вчитися, ставити цілі, їх досягати, використовувати свої знання для життя - це успішне майбутнє людини.

Продемонструвати картинку (стакан, наповнений до половини водою) та відповісти на запитання: що ви бачите на цій картинці?

На сьогоднішньому уроці ми розглянемо квадратичну функцію, графік якої можна утворити з графіка функції у = х², шляхом виконання одного або кількох геометричних перетворень.

 

ІV. Повторення  вивченого матеріалу.

§ 11 стор. 98-103

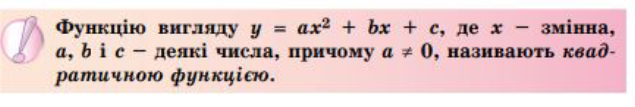
Якщо b=0 і с=0, тоді квадратична функція прийме вигляд у=ах².

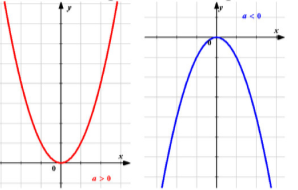
При а>0 вітки параболи направлені вгору,

при а<0 вітки параболи направлені вниз.

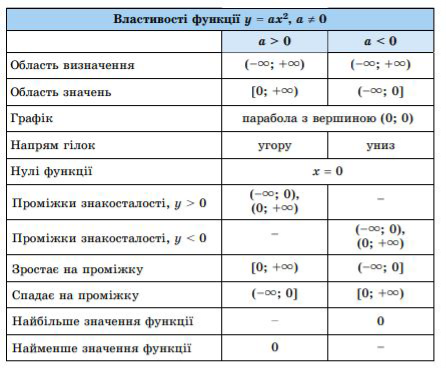
Властивості квадратичної функції.

То

Графік функції у = ах² + bх + с можна отримати з графіка функції у = ах² за допомогою двох перетворень – перенесень уздовж координатних осей. Графіком функції у = ах² + bх + с є парабола з вершиною в точці (х_в;у_в), де х_в=; у_в=f(х). Якщо а>0, гілки параболи направлені вгору, якщо а<0 – униз.

Будуючи графік функції у = ах² + bх + с, слід дотримуватися такої послідовності дій:

 

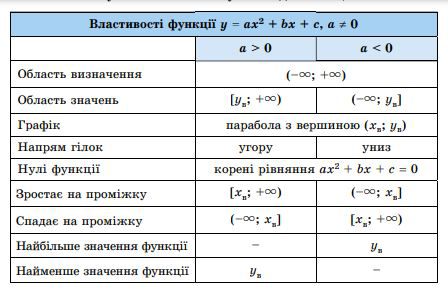
Пригадаємо властивості квадратичної функції.

V. Формування вмінь учнів розв'язувати задачі.

Письмові вправи:

Вправа 1  № 428, стор. 104 (розв’язування вправи на онлайн дошці з коментарем).

Вправа 2  Дано графіки функцій. Встановіть відповідність між графіками та формулами, що їх задають. Виправте помилки, щоб утворилися правильні відповідності.

 

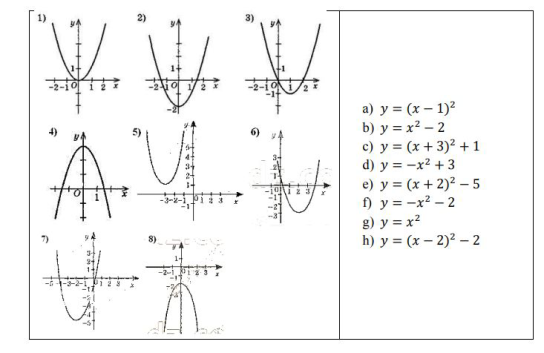
Вправа 3: Заповнити таблицю (Усно).

№	Квадратне рівняння:	Значення а	Значення b	Значення с	Дискримінант:	Визначити кількість коренів
1.	-3х2 - 4х + 2 = 0	-3	-4	2	D> 0	2
2.	х2 -2х + 1 = 0	1	-2	1	D= 0	1
3.	3х2- 7х + 6 = 0	3	-7	6	D < 0	0
4.	-х2 + 2х + 5 = 0	-1	2	5	D > 0	2
5.	5х2-2х + 7 = 0	5	-2	7	D< 0	0
6.	х2 + 10х + 4 = 0	1	10	4	D> 0	2
7.	х2 + 3х + 5 = 0	1	3	5	D< 0	0
8.	-4х2 + 12х + 9 = 0	-4	12	9	D=0	1
9.	х2 -5х = 0	1	-5	0	—	2
10.	-х2 -2 = 0	-1	0	-2	—	0
11.	-х2 = 0	-1	0	0	—	1
12.	х2 = 0	1	0	0	—	1

 

VІ. Удосконалення умінь і навичок.

Вправа 4.  На рисунку зображено графік функції

у = ах² + bх + с. Використавши подані на рисунку умови, укажіть: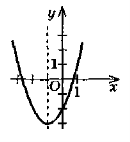

1.      знак числа а в рівнянні у = ах²+bх + с;
2.       координати вершини параболи;
3.       вісь параболи;
4.       напрям віток параболи.

 

VII. Підсумки уроку.

Запитання до класу:

-         Скільки нулів має функція, якщо a) D> 0, b) D= 0, c) D< 0?

-         Який напрям мають вітки параболи, якщо а > 0 та а < 0?

-         Як знайти вершину параболи і яке практичне застосування цієї формули?

 Домашнє завдання:

1.   Повторити §11 ст. 98-103.
2.   Виконати № 429(1), № 431(1), № 433(1). Користуйтеся матеріалом уроку.