Квадратний корінь. 8 клас. Закріплення
Підготувала: Гуляр Ольга Петрівна, учитель математики СЗШ № 47 м. Львова
Тема уроку. Функція ![]() її графік та властивості.
її графік та властивості.
Навчальна мета: Закріплювати означення арифметичного квадратного кореня з числа та властивості арифметичного квадратного кореня; Дати поняття про функцію виду ![]() та вчити їх характеризувати. Вправляти у використанній властивості функцій та будувати її графк.
та вчити їх характеризувати. Вправляти у використанній властивості функцій та будувати її графк.
Розвивальна мета:, розвивати вміння розв’язувати вправи, що передбачають побудову графіків, розв’язування рівнянь, розвивати вміння концентрувати увагу на виконанні завдання; підвищувати пізнавальну активність учнів.
Виховна мета: виховувати в учнях засобами уроку впевненість у своїх силах; математиучну культуру та мову.
Тип уроку: засвоєння нових знань, формування первинних вмінь.
Обладнання: робочі зошити (додаток 1), папки-тримачі, кольоровий скотч, мотузки, рулетка (5 м), маркери.
Форма проведення уроку: пленерний урок.
Місце проведення: подвір’я СЗШ № 47 м. Львова.
Очікувані результати: учні дають означення функції ![]() , будують її графік, називають її властивості.
, будують її графік, називають її властивості.
Хід уроку:
І. Організаційний етап
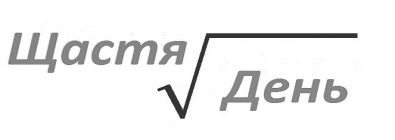 Перевірка готовності учнів до уроку, налаштування на роботу.
Перевірка готовності учнів до уроку, налаштування на роботу.
Кожен учень отримує робочий зошит (додаток 1).
Інтерактивна вправа.
Розгляньте картинку, вкажіть, чому саме так? Який математичний знак застосовано?
ІІ. Формулювання мети і завдань уроку

Учитель. Розгляньте, будь ласка, рисунок в робочих зошитах. Що ви на ньому бачите? (дерево з кореневою системою).
-Що символізує коріння в навколишньому світі? Для чого воно?( є опорою для рослин, рослини так живляться )
-З якою темою буде пов’язаний наш урок?(із темою «Квадратні корені»)
-Як ви думаєте, знання теми «Квадратні корені» є одними з основних знань у алгебрі? Чому?
Сьогодні на уроці, ми познайомимось із функцією ![]() , її графіком, властивостями.
, її графіком, властивостями.
III. Актуалізація опорних знань
Завдання «Склади відповідність»
|
Номер завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Завдання |
|
|
|
|
|
|
|
|
|
|
Варіант відповіді |
А)25 |
Б)5 |
В)7 |
Г)2 |
Д)11 |
Е) |
Є) |
Ж)0,2 |
З)5 |
Ключі: 1-В; 2-Д; 3-З; 4-Е; 5-Є; 6-Ж; 7-Г; 8-Б; 9-А.
Вчитель пропонує учням скласти відповідність на час( орієнтовно 3 хв)
Виконання усних вправ
(Необхідно вказати правильний знак нерівностей)
-
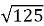 □ 5
□ 5
-
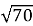 □ 8
□ 8
-
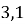 □
□ 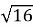
-
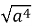 □ a
□ a
-
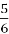 □
□ 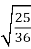
-
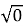
 0.1
0.1
-
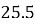 □
□ 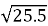
-
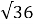 □
□ 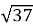
Відповіді: 1) >; 2) >; 3)<; 4)>; 5)=; 6)<; 7)<; 8)<.
IV. Засвоєння нових знань
1. Пропедевтична вправа
Завдання.
- За якою формулою ми можемо виразити сторону ![]() даного квадрата? (
даного квадрата? ( ![]()
- Чи буде змінюватись довжина сторони із зміною площі? ( так, із збільшенням довжини сторони збільшується площа)
- Чи буде єдиному значанню площі відповідати єдине значення сторони?(так)
- Чи можна перейти від прийнятих позначень функції і аргументу до певного виду функції?(так)
Перейшовши до прийнятих позначень функції і аргументу, маємо функції ![]()
2. Побудова графіка функції
Оскільки нам не відомо, як виглядає графік функції, то побудуємо його по точках. Складемо таблицю значень функції ![]() для кількох значень аргументу:
для кількох значень аргументу:
|
|
0 |
1 |
4 |
9 |
16 |
|
|
0 |
1 |
2 |
3 |
4 |
Побудуємо ці точки на координатній площині, створеній кольоровим скотчем на корфбольному полі (роль точок відіграватимуть учні, які займають положення відповідно до їх координат), та в робочих зошитах (див. рисунок). Переконуємося візуально на координатній площині, що на корфбольному полі (учні не перекривають один одного).
Через ці точки проведемо плавну криву: на корфбольному полі – учні беруться за руки, в робочих зошитах – рисуємо олівцем. Учитель звертає увагу на те, що початок графіка в точці (0;0) і графіком є вітка параболи. У робочих зошитах – продовжити графік за «крайню праву» точки. Отримали фігуру – графік функції ![]() за умови, коли для кожного невід’ємного значення
за умови, коли для кожного невід’ємного значення ![]() і відповідне значення
і відповідне значення ![]()
3. Визначення властивостей функції
Областю визначення є множина всіх невід’ємних дійсних чисел;
Областю значень функції є теж множина невід’ємних дійсних чисел;
Графіком є вітка параболи;
Графік проходить через початок координат і розміщений в І чверті
координатної площини.
4. Історична довідка.
Поняття квадратного кореня з чисел відоме ще з часів Вавилону та Єгипту, де були знайдені правила для їх наближеного обчислення. Знання єгиптян про корені вміщуються у декількох невеликих і двох великих папірусах. Це датується 2000р. до н.е. Пошук сторони квадрата за його площею, змусив помічників фараонів «підійти» до створення розділу математики про квадратні корені. У Вавилоні були складені таблиці квадратів чисел і величини квадратних коренів із числа. Герон Олександрійський детальніше підійшов до вивчення давного питання та у І ст. до н.е. описав процес добування квадратних коренів.
У Середньовіччі математик Кардано позначав квадратний корінь символом R або комбінацією Rx (бо Radix з латинської - корінь).
Сучасне позначення ввів німецький математик Крістоф Рудольфф в 1525 році. Походить цей символ від першої літери того ж слова radix. Риска над підкореневим виразом спочатку була відсутня; її пізніше ввів Рене Декарт (1637) для іншої мети (замість дужок), і ця риска незабаром злилася зі знаком кореня.
V. Формування вмінь
-
Задача 1. Чи належать графіку функції
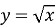 точки:
точки:
1 група: А(0;0), B(6;6), C(16;4), D(4;16);
2 група: A(25;5); B(5;25); C(0.25;5), D(0.25;0.5);
3 група: F(0;0); N(10;100); S(100;10); Z(36;6);
4 група: M(0.16;0.4); I(1;-1); P(1;1); A(64;8);
Відповіді:
1 група: A належить, В не належить, С належить, D не належить;
2 група: A належить, В не належить, С не належить, D належить;
3 група: F належить, N не належить, S належить, Z належить;
4 група: M належить, I не належить, P належить, A належить.
Задача 2.
Учні об’єднуються у чотири групи. Кожна група виконує завдання в своїй системі координат на корфбольному полі та в робочих зошитах.
Розв’яжіть графічно рівняння:
1 група: ![]()
2 група: ![]()
3 група: ![]()
4 група: ![]()
Відповіді:
1 група :
Побудуємо два графіки функцій ![]() та
та ![]() на одній координатній площині.
на одній координатній площині.
|
|
1 |
0 |
|
|
6 |
1 |
|
|
0 |
1 |
4 |
9 |
|
|
0 |
1 |
2 |
3 |
2 група:
Побудуємо два графіки функцій ![]() та
та ![]() на одній координатній площині.
на одній координатній площині.
|
|
1 |
0 |
|
|
4 |
1 |
|
|
0 |
1 |
9 |
16 |
|
|
0 |
1 |
3 |
4 |
3 група:
Побудуємо два графіки функцій ![]() та
та ![]() на одній координатній площині.
на одній координатній площині.
|
|
1 |
2 |
|
|
2.5 |
4 |
|
|
0 |
1 |
4 |
9 |
|
|
0 |
1 |
2 |
3 |
4 група:
![]()
Побудуємо два графіки функцій ![]() та
та ![]() на одній координатній площині.
на одній координатній площині.
|
|
1 |
2 |
|
|
3 |
5 |
|
|
0 |
1 |
4 |
9 |
|
|
0 |
1 |
2 |
3 |
3 завдання: Користуючись графіком функції ![]() знайдіть:
знайдіть:
А) значення функції, якщо значення x дорівнюють: 0,25; 2; 3; 4;
Б) значення x, якщо значення функцції дорівнюють: 1; 0; 4; -16
Відповіді:
А)
|
|
0.25 |
2 |
3 |
4 |
|
|
0.5 |
|
|
2 |
Б)
|
|
1 |
0 |
16 |
- |
|
|
1 |
0 |
4 |
-16 |
4 завдання:
В одній системі координат побудуйте графіки функцій:
1група: y= ![]() і y= -
і y= - ![]()
2група: y=3 ![]() і y=
і y= ![]()
3група y= ![]() і y= -
і y= - ![]()
Відповіді:
1 група:
![]()
|
|
0 |
1 |
4 |
9 |
|
|
0 |
1 |
2 |
3 |
![]()
|
|
0 |
1 |
4 |
9 |
|
|
0 |
-1 |
-2 |
-3 |
2 група:
![]()
|
|
0 |
1 |
4 |
9 |
|
|
0 |
3 |
6 |
9 |
![]()
|
|
0 |
1 |
4 |
9 |
|
|
0 |
1 |
2 |
3 |
3 група:
![]()
|
|
0 |
1 |
4 |
9 |
|
|
0 |
|
1 |
1.5 |
![]()
|
|
0 |
1 |
4 |
9 |
|
|
0 |
|
-1 |
-1.5 |
5 завдання: Розв’яжіть рівняння.
1група: ![]() – 8 = 0
– 8 = 0
2група: ![]() + 8 = 0
+ 8 = 0
3група: ![]() – 3 = 0
– 3 = 0
4група: ![]() – 3 = 0
– 3 = 0
Відповіді:
1група: : ![]() – 8 = 0
– 8 = 0
![]() = 8
= 8
x = 64
2група: ![]() + 8 = 0
+ 8 = 0
![]() = -8
= -8
Розв’язків немає.
3група: ![]() – 3 = 0
– 3 = 0
![]() = 3
= 3
x = 9![]()
4група : ![]()
![]()
![]()
x = 16.
VI. Підсумок.
1. Бесіда.
- Як встановити, що точка належить графіку?
- Як ви можете охарактеризувати властивості функції ![]() ?
?
- Як графічно розв’язувати рівняння?
- Як будувати графік за точками?
- Чим є графік функції ![]() ?
?
2. Рефлексія.
 На ключику, що символізує «ключ термінів до теми», напишіть терміни, які ви закріпили та вивчили на сьогоднішньому уроці. (Відповіді коментують)
На ключику, що символізує «ключ термінів до теми», напишіть терміни, які ви закріпили та вивчили на сьогоднішньому уроці. (Відповіді коментують)
Варіанти відповідей: функція, аргумент, змінна, графік, парабола, вітка параболи, область значень, корінь.


про публікацію авторської розробки
Додати розробку
