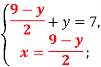«Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки»

Конспект уроку

на тему:

«Розв’язування систем двох лінійних рівнянь з двома

змінними способом підстановки»

Підготувала вчитель-методист Кременецької ЗОШ  І-ІІІ ст. №1

ім.Галини Гордасевич Алкіна Галина Володимирівна

Тема. Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки

Мета:

навчальна:

•          ознайомити учнів із розв’язуванням системи лінійних рівнянь із двома змінними способом підстановки;
•          сформувати вміння учнів розв’язувати системи лінійних рівнянь із двома змінними способом підстановки за допомогою алгоритму;

розвивальна:

•          формувати вміння володіння математичними термінами;
•          розвивати основні процеси мислення;

виховна:

•          виховувати культуру математичних записів;
•          виховувати позитивне ставлення до навчання.

Тип уроку: урок формування нових знань, умінь та навичок.

Обладнання та наочність: підручник з алгебри за 7 клас, автор: Істер, Нова програма

Хід уроку

1. Організаційний момент (5-7 хв)

• Налаштовування на роботу.
• Перевірка домашнього завдання:

(§27 № 1010(2, 4), 1014(2), 1016(2))

№1010. Розв’яжіть систему рівнянь графічно:

2)

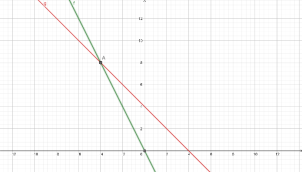
Прямі перетинаються в точці (-4;8). Отже, пара чисел (-4;8) є розв'язком системи

4)                    

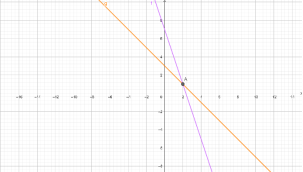
Прямі перетинаються в точці (2;1). Отже, пара чисел (2;1) є розв'язком системи

№1014. Розв’яжіть систему рівнянь графічно:

2)

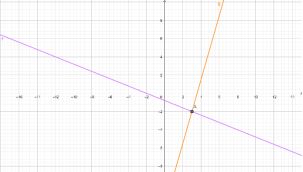
Прямі перетинаються в точці (3;-2). Отже, пара чисел (3;-2) є розв'язком системи

№1016. Чи має система розв’язки і скільки?

2)                  

, ,

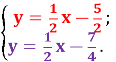
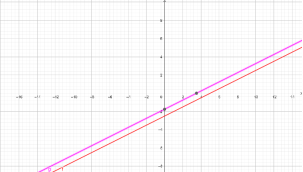
Оскільки , то прямі і паралельні. Отже, система розв’язків не має.

• Повідомлення теми і мети уроку.

2. Актуалізація опорних знань (5-7 хв)

Повторимо поняття, які нам будуть потрібні сьогодні на уроці. Для цього виконаємо наступні завдання.

     1. Розкрийте дужки і спростіть вираз:

1.     = = ;
2.     = = ;
3.     = = ;
4.     = = .

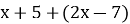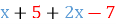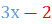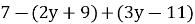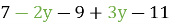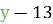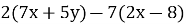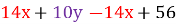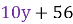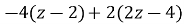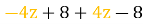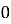     2. Виразіть змінну x через y із рівняння:

1. ,

;

2. ,

,

;

3. ,

;

4. ,

,

.

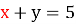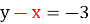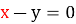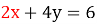    3. Виразіть змінну y через x із рівняння:

1. ,

;

2. ,

,

,

;

3. ,

,

,

;

4. ,

,

.

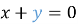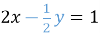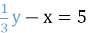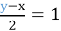3.  Вивчення нового матеріалу (5-7 хв)

1. Розв’язування системи лінійних рівнянь із двома змінними способом підстановки.

(Розглянути разом з учнями розв’язання способом підстановки системи рівнянь . Звернути їхню увагу на те, що основна мета виконуваних перетворень — отримати рівняння, яке міститиме тільки одну змінну)

Графічний спосіб розв’язування систем рівнянь є досить громіздким і до того ж не завжди допомагає знайти точні розв’язки. Розглянемо інші (не графічні) способи розв’язування систем лінійних рівнянь з двома змінними, які називають аналітичними. На сьогоднішньому уроці ми ознайомимось із способом підстановки.

Розглянемо приклад. Розв’яжемо системи рівнянь   (1)

Розв’язання

Виразимо з другого рівняння змінну x через змінну y: . Підставимо в перше рівняння системи замість змінної x вираз . Отримаємо систему рівнянь                (2)

Перше рівняння отриманої системи має тільки одну змінну y. Розв’яжемо рівняння: ; ; ; .

Підставимо замість число 2 у рівність , отримаємо:

; . Пара є розв’язком системи (2).

Ця сама пара є розв’язком системи (1), оскільки числові рівності

  і   є правильними.

2. Поняття рівносильних систем рівнянь із двома змінними.

Системи рівнянь із двома змінними називають рівносильними, множини розв’язків яких співпадають. Системи, які не мають розв’язків, також рівносильні.

Розв’язуючи попередню систему способом підстановки, ми замінювали систему (1) на рівносильну їй систему (2), одне з рівнянь якої містить одну змінну.

3. Алгоритм розв’язування системи лінійних рівнянь із двома змінними способом підстановки.

Щоб  розв’язати  систему  лінійних  рівнянь  способом  підстановки, потрібно:

4.         Закріплення нового матеріалу (20 хв)

1. Виконання усної вправи.

(§28 № 1029)

№1029. У якій з рівностей 1)-3) правильно виконано підстановку для розв’язування системи рівнянь

1) ;

2) ;

3) .

Відповідь: .

2. Виконання письмових вправ.

(§28 № 1031(1), 1034(1, 3, 4), 1038(2), 1040(1))

№1031. Розв’яжіть систему рівнянь способом підстановки:

1)

    ;

    ;

    ;

    ;

    ;

    .

Відповідь: .

№1034. Знайдіть розв’язок системи

1)

Відповідь: .

2)

;

Відповідь: .

3)

Відповідь:

№1038. Розв’яжіть систему рівнянь:

  2)

;

;

;

;

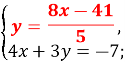
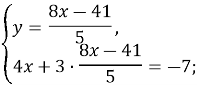
Відповідь: .

№1040. Знайдіть розв'язок системи:

1)

Відповідь: .

5. Висновки (3 хв)

На уроці ми ознайомились із розв'язуванням  системи лінійних рівнянь з двома змінними способом підстановки; розглянули метод підстановки розв'язування системи лінійних рівнянь з двома змінними; розглянули прості та більш складніші системи лінійних рівнянь з двома змінними, які потребують спрощення, користуючись алгоритмом. Також навчилися перевіряти чи правильно виконано підстановку для розв'язання системи рівнянь.

6.         Домашнє завдання (2 хв)

(§28 № 1030, 1033(1), 1035(2, 4), 1039(2), 1041(2))