Розв'язування тригонометричних рівнянь зведенням до однієї тригонометричної функції

Мета уроку:

• Ознайомити учнів з методикою розв'язування тригонометричних рівнянь за допомогою зведення до однієї тригонометричної функції.
• Навчити учнів визначати вираз, до якого слід звести вихідне тригонометричне рівняння.
• Практикувати учнів у застосуванні отриманих знань на різних прикладах.
• Формувати в учнів уміння розв’язувати тригонометричні рівняння, розвивати логічне мислення

Матеріали для уроку:

• Презентація з основними концепціями та прикладами.
• Роздатковий матеріал з прикладами для практичної роботи.
• Зошити або аркуші для самостійної роботи учнів.

Хід уроку:

Епіграф уроку:

Ми ніколи не станемо

математиками,

навіть знаючи напам’ять

всі чужі доведення,

якщо наш розум нездатний

самостійно розв’язувати,

які б то не було проблеми.

Рене Декарт

Повторення вивченого матеріалу: (5 хвилин):

     Якою формулою записується розв’язок рівняння cos x = α, cos x = 0,  

cos x = 1, cos x = -1?

     При якому значенні α рівняння cos x = α має розв’язок?

     Якою формулою записується розв’язок рівняння sin x = α, sin x = 0,  

sin x = 1, sin x = -1?

     При якому значенні α рівняння sin x = α має розв’язок?

     Якою формулою записується розв’язок рівняння tg x = α, tg x = 0?

     Якою формулою записується розв’язок рівняння сtg x = α, сtg x = 0?

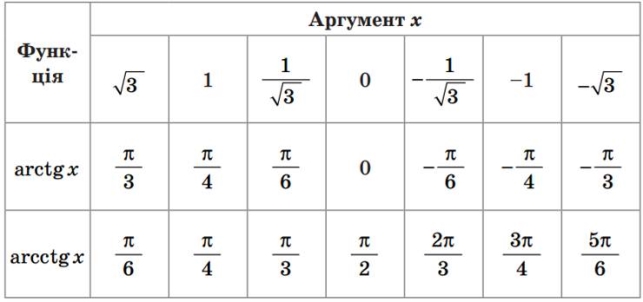
Пригадаємо деякі значення

Практична частина (10 хвилин):

Розв'язання кількох прикладів з різними типами тригонометричних рівнянь зведенням до однієї тригонометричної функції.

Запитання учнів і вирішення непорозумінь.

Самостійна робота (10 хвилин):

А) sinx = ;

Б) cos x = ;

В) cosx – 1  = 0;

Г) tg2x = 1.

Теоретичний блок (15 хвилин):

Пояснення методу зведення до однієї тригонометричної функції на прикладі кожного з типових тригонометричних рівнянь.

Виведення основних підходів до зведення до однієї функції (наприклад, заміна тригонометричних функцій, використання тригонометричних тотожностей).

Приклад 1. Розв’язати рівняння

2 x + sin x – 1 = 0.

Розв’язання.

Введемо нову змінну t=sinx. Тоді дане рівняння буде мати вигляд 2t² + t – 1 = 0.

D=1+8=9, =3, t₁ = = , t₁ = = -1,

Тому, sin x =                         або                  sin x= -1 

x= (-1)ⁿ arcsin +πn, n Є Z,                             x= - +2πk, k Є Z.

x= (-1)ⁿ  +πn, n Є Z

Приклад 2.

Розв’язати рівняння

6sin²x + 5 cosx – 2 = 0.

Розв’язання

Замінимо sin²x на 1-cos²x, отримаємо квадратне рівняння відносно cosx.

6(1 – cos²x) + 5 cosx – 2 = 0,

-6 cos²x + 5 cosx + 4 = 0,

6 cos²x – 5 cosx – 4 = 0.

Нехай cos x = t, тоді 6t²-5t-4=0,

t_{1 = -} ,  t_{2 =}

Отже, cosx= -   або cosx = .

Розв’яжемо рівняння cosx= - , маємо:

X = ± + 2πn, n Є Z.

Рівняння cosx = не має розв’язку, або >1.

Учні розв'язують певну кількість вправ на зведення до однієї тригонометричної функції самостійно.

1. cos2x = 7-8 sinx
2. 2cos²3x + sin (- 3x) – 1 = 0.

Підсумок (5 хвилин):

Які методи розв’язування тригонометричних рівнянь ми сьогодні розглянули на уроці?

• Чи досягли ми мети уроку?
• Для чого нам потрібні ці знання?
• Пояснення основних ідей і важливих моментів.
• Завдання на наступний урок або додаткові вправи для закріплення.

Домашнє завдання:

Завдання на вправу з розв'язування тригонометричних рівнянь зведенням до однієї тригонометричної функції.

cos2x – sinx = 0

tgx + 5 ctgx = 6

Додаткові завдання для практики.