Розв'язування вправ на застосовування теореми синусів і косинусів та наслідків із них.

Тема уроку. Розв'язування вправ на застосовування теореми синусів і 

                       косинусів та наслідків із них.

Мета уроку: формування вмінь учнів застосовувати теореми синусів і косинусів та наслідків із них до розв'язування задач.

Тип уроку: комбінований.

Наочність і обладнання: таблиця «Співвідношення між сторонами і кутами трикутника»[13].

Вимоги до рівня підготовки учнів: застосовують теорему синусів до розв'язування задач.

Хід уроку

І. Перевірка домашнього завдання

Фронтальне опитування

1. Сформулюйте теорему про співвідношення між кутами три­кутника і протилежними сторонами.
2. Сформулюйте обернену теорему (теорему про співвідношення між сторонами трикутника і протилежними кутами).
3. Усна перевірка задачі № 1 за запитаннями.

а) Які сторони лежать проти кутів А, В, С?

б) Яка із сторін трикутника є найбільшою? Чому?

в) Яка із сторін трикутника є найменшою? Чому?

г) Чи може даний трикутник бути рівнобедреним? Чому?

Усна перевірка задачі № 2 за запитаннями

а) Які кути лежать у трикутнику ABC проти сторін АВ, ВС, АС відповідно?

б) Який із кутів трикутника є найбільшим? Чому?

в) Який із кутів трикутника є найменшим? Чому?

Перевірка розв'язування задачі № 3

(за записами на дошці, зробленими до початку уроку)

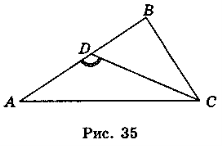Один із кутів (рис. 35), ADC або CDB, негострий. (?)

Нехай для визначеності ADС ≥ 90°, тоді     A < 90°. (?)

Із трикутника ADC маємо: DC < AC (?)

Отже, відрізок CD менший хоча б за одну із сторін — АС або ВС.

[Знак (?) означає, що учні повинні пояснити: чому це так (зробити посилання на відповідні означення, теореми тощо).]

II. Закріплення й осмислення вивченого матеріалу

Розв'язування задач

1. Визначте вид трикутника (відносно кутів), якщо його сторони дорівнюють 11 см, 17 см, 21 cm.

Розв'язання

Нехай а = 11 см, b = 17 см, с = 21 см. Найбільшим кутом буде кут С, оскільки він лежить проти більшої сторони. Тоді с² = 21² = 441, а² + b² = 11² +   + 17² = 121 + 289 = 410. Оскільки с² > а² + b², то трикутник тупокутний.

Відповідь. Тупокутний.

2. Визначте вид трикутника (відносно кутів), у якого сторони відносяться як: а) 4 : 2 : 3;              б) 4 : 5 : 3;                в) 3 : 3 : 4.

Відповідь, а) Тупокутний; б) прямокутний; в) гострокутний.

Колективне розв'язування задачі

1. Знайдіть радіус кола, описаного навколо трикутника із сторо­нами 5 м,     6 м, 7 м.

Розв'язання

Нехай а = 5 м, b = 6 м, с = 7 м, тоді за теоремою косинусів маємо:

с² = a² + b² – 2abcosC; 49 = 25 + 36 – 2 ∙ 5 ∙ 6 ∙ cosC ; 49 = 61 – 60cosC; 60cosC = 12; cosC = .

За основною тотожністю cos²C + sin²C = 1 маємо:

+ sin²C = 1; sin²C = 1 – = , звідси sinC = = .

Тоді за теоремою синусів маємо: ; ; 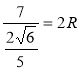R = м.

Відповідь. м.

ІІІ. Самостійна робота

Варіант 1

1. Знайдіть радіус кола, описаного навколо трикутника, у якому
   сторона дорівнює 2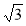 см і лежить проти кута 120°.

(4 бали)

2. У трикутнику ABC відомо, що ВС = 2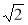см, 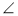A = 45°, 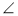C = 30°. Знайдіть сторону АВ.

(4 бали)

3. У трикутнику ABC кути А, В, С відносяться як 4 : 2 : 3, ВС = 4 см. Знайдіть сторону АВ.

(4 бали)

Варіант 2

1. Знайдіть радіус кола, описаного навколо трикутника, у якому сторона дорівнює 2 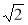см і лежить проти кута 135°.

(4 бали)

2. У трикутнику ABC відомо, що АВ = 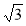см, ВС = 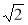см, 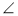C = 120°. Знайдіть кут А.

(4 бали)

3. У трикутнику ABC кути А, В, С відносяться як 4 : 2 : 3, ВС = 4 см. Знайдіть сторону АС.

(4 бали)

Відповіді до завдань самостійної роботи

Варіант 1. 1. 2 см. 2. 2 см. 3. (см).

Варіант 2. 1. 2 см. 2. 45°. 3. (см).

IV. Домашнє завдання

Розв'язати задачу.

Дано три сторони трикутника: а = 1, b = 2, с = 8. Знайдіть його кути.

V. Підбиття підсумків уроку

Запитання до класу

1. а : b : с = 2 : 3 : 4. Як відносяться синуси кутів трикутника?
2. Синуси кутів трикутника відносяться як 3 : 4 : 5. Як відносять­ся сторони трикутника? Визначте вид трикутника (за кутами).