Розв'язування задач для підготовки до предметних олімпіад

Про матеріал

Рекомендована підбірка задач допоможе для підготовки учнів до предметних олімпіад з математики, а також для створення матеріалів для їх проведення з 6 класу по 11 клас. Всі вправи містять розв'язки

Перегляд файлу

Підготовка до олімпіади.

Розв’язування олімпіадних задач

6 клас

1. Із книги випала частина, перша сторінка якої має номер 619, а номер останньої записується тими ж цифрами в деякому іншому порядку. Скільки сторінок у втраченій частині книги? Відповідь обґрунтуйте.

2. Максим записав на дошці деяке число, яке закінчується цифрою 4 і усі цифри якого різні. Він зауважив, що якщо останню цифру переставити на початок , то отримаємо число в 4 рази більше за початкове. Яке число Максим записав на дошці? Відповідь обґрунтуйте.

3. Для того, щоб виготовити три буханки хліба, необхідно виготовити закваску з трьох літрів води та муки, яка становитиме 5/8 від всієї закваски. Яку найбільшу кількість буханок хліба можна виготовити, використавши чотири літри муки?

4. У Святослава був набір з шести гирьок масою 1 кг, 2 кг, 3 кг, 4 кг, 5 кг, 6 кг, причому чим важча була гирька, тим більший був її розмір. Одну з гирьок він загубив. Чи зможе Святослав визначити масу гирьки, яку він загубив, використовуючи лише шалькові терези? Відповідь обґрунтуйте.

Розв’язки завдань

Розв’язання: Зауважимо, якщо номер першої сторінки у втраченій частині книги є непарним числом, то номер останньої повинен бути парним. Причому номер останньої повинен бути числом більшим за 619 і повинен складатися з тих самих цифр, що і 619. Єдиним таким числом є число 916. Тому у втраченій частині книги 916 – 619 + 1 = 298 сторінок.

Відповідь: 298 сторінок.

Розв’язання: Запишемо той факт, якщо останню цифру числа переставити на початок, то отримаємо число в 4 рази більше, у вигляді ребуса:

-----------------

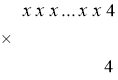
Тоді легко зауважити, що передостання цифра числа, що задумав

Максим, – 6, третя з кінця 5 і т.д. Такий аналіз можна продовжити доти,

доти ми не отримаємо цифру 4 або доки цифри отриманого числа

будуть різними.

Відповідь: 102564.

Розв’язання:

– кількість літрів закваски, необхідних для

виготовлення трьох буханок хліба;

8 – 3 = 5 (л) – кількість літрів муки, необхідних для виготовлення трьох

буханок хліба.

Тому з чотирьох літрів муки можна виготовити буханки

хліба.

Відповідь: дві буханки.

Розв’язання: Насправді, Святославові достатньо двох зважувань. Пронумеруємо гирьки, що залишилися у нього числами від 1 до 5, починаючи з найлегшої та закінчуючи найважчою. На ліву шальку терезів поставимо гирьки з номерами 2 та 3, а на праву з номером 5.

Якщо терези покажуть =, то маса гирьки, яку забрали, 3 кг або 6 кг. При другому зважуванні на ліву шальку терезів поставимо гирьки з номерами 1 та 2, а на праву з номером 3. Якщо терези покажуть:

а) =, то забрали гирьку, маса якої 6 кг;

б) <, то забрали гирьку, маса якої 3 кг.

Якщо терези показують >, то маса гирьки, яку забрали, 1 кг або 2 кг. При другому зважуванні на ліву шальку терезів поставимо гирьки з номерами 2 та 3, а на праву з номером 4. Якщо терези покажуть:

а) >, то забрали гирьку, маса якої 5 кг;

б) =, то забрали гирьку, маса якої 4 кг.

Відповідь: зможе.

7 клас

1. Василина, Галина і Ярина хотіли придбати по одному однаковому капелюшку кожна. Василині не вистачило третини його вартості, Галині – четвертої частини, а Ярині – однієї п’ятої частини. Коли ціну капелюшка зменшили на 47 грн, подруги об’єднали свої кошти і прибрали три такі капелюшки без решти. Скільки коштував капелюшок до подешевшання?

2. Чи існують натуральні числа , які задовольняють рівність:

3. Чи можна на папері намалювати 6 кіл так, щоб вони перетиналися у 36 точках? Відповідь обґрунтуйте.

4. Є 9 гир вагою 1г, 2г, ..., 9г. Андрій та Олена по черзі беруть гирі і кладуть їх на ваги зі стрілкою, не знімаючи попередні. Якщо після чергової гирі стрілка покаже вагу більше 25г, то той, хто поклав цю гирю, програв. Хто може перемогти в цій грі, якщо кожний намагається перемогти та першій хід робить Андрій?

Розв’язки завдань

1. Розв’язання: Нехай х – це вартість одного капелюха до подешевшання. Тоді у Анни було , у Василини , а у Галини . Тому Отже, х = 180 грн.

Відповідь: 180 грн.

2. Розв’язання: Припустимо, що це можливо, тоді маємо, що – парні. Якщо обидва або рівно одне з них непарне, то ліва частина рівності – непарна, а права – парна, тому рівність неможлива. Але, якщо – парні, то ліва частина кратна , а права не кратна . Одержана суперечність завершує доведення.

Відповідь: не існують.

3. Розв’язання: Зауважимо, що довільна пара кіл може перетинатися не більше, ніж у двох точках. Тоді кожне з шести кіл перетинає інші не більше, ніж в 25 = 10 точках. Тому загальна кількість точок перетину не перевищує 610 = 60 точок, проте кожну з точок ми порахували двічі, тому кількість точок перетину не перевищує 60 : 2 = 30, суперечність умові.

Відповідь: не можна.

4. Розв’язання. Першим ходом Андрій кладе гирю вагою г. А далі просто якщо Олена вибирає гирю вагою г, то він вибирає гирю, вагою г. Так після його третього ходу на шальках буде рівно г і Олеся програє наступним ходом.

Відповідь: перемагає Андрій.

8 клас

1. Капітан Джек Горобець і його піратська команда викопали кілька золотих монет і поділили їх порівну. Якщо б піратів було на чотири менше, то кожний з них отримав би на 10 монет більше. Якщо б монет було на 50 менше, то кожний з них отримав би на 5 монет менше. Скільки монет викопали пірати?

2. Ненульові числа задовольняють умови:

Чому може дорівнювати значення виразу ?

3. Скільки існує натуральних , для яких число є точним квадратом цілого числа?

4. Знайдіть усі пари дійсних чисел , що задовольняють рівності:

5. Нехай АВС – рівнобедрений гострокутний трикутник ( АВ = ВС). На стороні ВС відмітили точку Р таку, що РАС = 45^о, а Q – точка перетину серединних перпендикулярів до відрізка АР зі стороною АВ. Довести, що PQ ВС.

Розв’язки завдань

1. Розв’язання. Нехай, n – кількість піратів, а х – кількість монет, отриманих кожним піратом. Тоді звідки . Крім того, , звідки . Отже, у команді було 10 піратів, кожний з них отримав по монет, а всього монет було .

Відповідь: 150 монет.

2. Розв’язання. З умови задачі маємо, що . Оскільки , то . Враховуючі, що , маємо, що

Відповідь: .

3. Розв’язання. Очевидно, що число може бути точним квадратом тільки непарного числа. Якщо , то його квадрат . Тобто усі квадрати непарних чисел задовольняють потрібну умову, тому залишається порахувати скільки є квадратів непарних чисел між числами та . Найменше з них , найбільше – , тому їх неважко порахувати, що їх .

Відповідь: .

4. Розв’язання. Домножимо рівняння на і згрупуємо певним чином доданки:

та .

Відповідь: .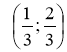

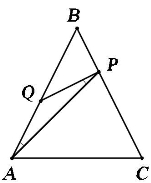5. Доведення.

Оскільки Q лежить на серединному перпендикулярі до відрізка АР, то трикутник АQP рівнобедрений. Нехай

QАР = QРА = .

Тоді ВQА = 2 як зовнішній кут трикутника АQP, ВАС = 45^о + та АВС = 180^о – 2ВАС = 180^о – 2(45^о + ) = 90^о - 2.

Отже, QВР = 90^о – 2= 90^о – ВQР.

Тому трикутник ВQР прямокутний, тобто РQ ВС.

9 клас

1. Марко, зігравши 40 партій у шаховому турнірі, отримав 25 очок. За перемогу в партії гравцю нараховується 1 очко, за нічию – 0,5 очка, за поразку – 0 очок. На скільки партій більше хлопець виграв, ніж програв?

2. Чому дорівнює сума цифр числа ?

3. Відрізки та – відповідно медіана та висота гострокутного трикутника . Відомо, що та . Знайдіть довжину сторони .

4. Натуральні числа задовольняють умови: та . Чому може дорівнювати значення виразу ?

5. Двоє по черзі знімають зі столу фішки. За один раз дозволяється зняти зі столу 1. 10 або 11 фішок. Виграє той, хто зніме останню фішку. Перед початком гри на столі було 40 фішок. Хто виграє за умови дотримання правил гри – той, хто починає гру, чи його суперник?

Розв’язки завдань

1. Розв’язання. Нехай х – це кількість перемог, y – це кількість нічий, z – кількість поразок, тоді , Тоді і Отже, .

Відповідь: на 10.

2. Розв’язання. Зробимо такі обчислення:

Залишається порахувати суму цифр одержаного числа: 2019(4 + 5) + (3 + 6) = 18180.

Відповідь: 18180.

3. Розв’язання. Відрізок – медіана прямокутного , тому він дорівнює половині гіпотенузи, звідки та трикутник – рівнобедрений. Тому . З іншого боку, як зовнішній кут у . Тому , звідки – також рівнобедрений. Таким чином .

Відповідь: .

4. Розв’язання. Із заданих умов запишемо, що , тому . Тоді з нерівності . Аналогічно . Таким чином є дві можливості. Якщо , то - звідси - не ціле. Якщо , то - звідси . Таким чином .

Відповідь: .

5. Розв’язання. Будемо розв’язувати задачу з кінця. Якщо припустити, що на столі залишилася одна фішка, то ситуація є виграшною для того гравця, чия черга ходити. Він бере цю фішку й виграє. Якщо залишилось дві фішки – ситуація програшна для того, чия черга ходити. Будемо записувати числа 1, 2, 3, … зі знаками «+» або «–» залежно від того, виграшною чи програшною є дана ситуація для гравця, який робить хід. Тоді якщо гравець певним ходом (знявши 1, 10 або 11 фішок) може створити програшну ситуацію для свого суперника (або його черга ходити), то для нього початкова ситуація є виграшною. Тепер можна з’ясувати по черзі для всіх чисел 1, 2, 3, … виграшною чи програшною є ситуація для даної кількості фішок на столі. Для чисел від 1 до 9 знаки «+» або «–» розставляються по черзі. Числа 10, 11, 12, 13, …, 19 є виграшними, 20 – програшним (будь – яким ходом можна досягнути лише чисел 9, 10 і 19, які є виграшними для суперника). Помітивши закономірність (знаки через 20 чисел повторюються), можемо легко продовжити розставляння знаків. Неважко переконатися, що число 40 має знак «–», тобто за правильної гри другий гравець виграє.

Відповідь: Виграє другий гравець.

10 клас

1. Автомобіль вирушив з міста A з швидкістю 50 км/год. Через годину за ним виїхав другий автомобіль зі швидкістю 51 км/год, ще через годину – третій зі швидкістю 52 км/год і т. д. Останній 51-ий автомобіль вирушив з міста А зі швидкістю 100 км/год через 50 годин після того, як вирушив перший. З якою швидкістю їхав автомобіль, який очолював колону через 100 годин після старту першого автомобіля? (Усі автомобілі їхали з постійними швидкостями.).

2. Відомо, що банани, 7 яблук та 1 ананас коштують 329 грн. 4 банани, 10 яблук та 1 ананас коштують 441 грн. Скільки коштують разом банан, 1 яблуко та 1 ананас?

3. Знайдіть усі такі прості числа , для яких справджується рівність:

4. На гіпотенузі АВ прямокутного трикутника АВС відмітили довільну точку D. Коло, описане навколо трикутника АСD, вдруге перетинає пряму ВС у точці Е, а коло, описане навколо трикутника ВСD, вдруге перетинає пряму АС у точці F. Довести, що пряма ЕF проходить через точку D.

5. На столі лежать у ряд 50 карток, занумерованих у деякому порядку числами від 1 до 50. Двоє гравців по черзі забирають собі одну з крайніх карток, поки у кожного з них не опиниться по 25 карток. Виграє гравець, у якого сума номерів карток виявиться більшою, ніж у іншого. Чи має хтось з гравців виграшну стратегію? Якщо має, то хто?

Розв’язки завдань

1. Розв’язання. Через 100 годин після того, як з міста А вирушив перший автомобіль, кожен автомобіль проїхав (101 – n)(n + 49) км, де n – це номер, під яким він вирушив з міста А. Тому нам необхідно знайти таке натуральне , при якому вираз (101 – n)(n + 49) приймає найменше значення. Функція = (101 – х)(х + 49) – парабола з вітками вниз, яка досягає свого найбільшого значення в точці .

Отже, через 100 годин після того, як з міста А вирушив перший автомобіль, колону очолював автомобіль, що вирушив з міста 26-м, зі швидкістю 75 км/год.

Відповідь: 75 км/год.

2. Розв’язання. Позначимо вартість банана через , яблука -- та ананаса -- . Тоді

та .

Тоді

Відповідь: .

3. Розв’язання. Спочатку просто знайдемо усі трійки простих чисел, без сортування за зростанням, що задовольняють умови задачі. Оскільки -- просте число, то нехай . Тоді маємо рівність або . Залишається перебрати варіанти розкладу числа на множники: , при яких -- прості. Оскільки непарним може бути лише множник, що дорівнює , то маємо єдиний розв’язок: .

Відповідь: .

4. Розв’язання. Оскільки АСЕ = ВСF = 90^о, то АЕ та BF є діаметрами кіл, описаних навколо трикутників АСD та ВСD. Звідси АDЕ = ВDF = 90^о. Тому обидві прямі DЕ та DF є перпендикулярними до АВ, а отже збігаються.

5. Розв’язання. Розфарбуємо картки у чорний та білий колір так, щоб кольори чергувалися. Зауважимо, що серед чисел від 1 до 50 є 25 парних та 25 непарних, тому сума всіх чисел є непарною, отже суми чисел на чорних та білих картках не можуть виявитися однаковими. Нехай, наприклад, більшою є сума чисел на білих картках. Покажемо, що перший гравець може забрати всі білі картки собі. Справді, спочатку одна з крайніх карток біла, він може її взяти та обидві крайні картки стануть чорними. Другий гравець візьме чорну картку та знову одна з крайніх карток стане білою, і так далі. Таким чином, перший гравець збере всі білі картки та виграє. Якщо ж більшою є сума чисел на всіх чорних картках, то цілком аналогічно він збере всі чорні картки.

Відповідь: виграшну стратегію має перший гравець.

11 клас

1 Будь-які три вершини куба визначають трикутник. У скількох з цих трикутників не всі вершини належать одній грані?

2. Знайдіть усі трійки натуральних чисел, які задовольняють умови:

та .

3. Доведіть, що ні при яких натуральних значення виразу не є точним квадратом натурального числа.

4. У опуклого чотирикутника відомі довжини усіх сторін , , , та однієї діагоналі . Знайдіть довжину другої діагоналі.

5. Знайдіть усі такі функції , що визначені на множині дійсних чисел, які для довільних дійсних задовольняють рівність:

Розв’язки завдань

1. Усього є = 56 трикутників з вершинами у вершинах куба. Кожній грані куба належать 4 трикутники, тому шукана кількість трикутників дорівнює 56 – 6 4 = 32.

Відповідь: у 32 .

2. Розв’язання. Віднімемо від першого рівняння друге: або . Оскільки -- просте число, то можливі лише такі два варіанти:

та або та .

Якщо додати ці рівняння, то матимемо, що або .

Для першого випадку , тоді . Звідси маємо перший розв’язок та .

Для другого випадку , тоді . Звідси маємо другий розв’язок та .

Відповідь: два розв’язки : та

3. Доведення. Методом від супротивного, припустимо, що для деякого натурального . Тоді – непарне, і розглянемо останню рівність у такому вигляді:

У правій частині добуток двох послідовних парних чисел, а тому вона кратна . Для лівої частини по модулю маємо: , тоді ліва частина не кратна . Одержана суперечність завершує доведення.

4. Розв’язання. Застосуємо декілька разів теорему косинусів. З знаходимо, що

звідси . Аналогічно з :

, .

Тепер з знаходимо остаточно, що

Відповідь: .

5. Розв’язання. Якщо підставити , то отримаємо, що . Далі покладемо і будемо мати, що , звідки . Перевіркою переконуємось, що ця функція задовольняє умови.