«Розв'язування задач на ознаки рівності трикутників»

«Розв'язування задач на озна­ки рівності трикутників» 

Мета:

- повторити, систематизувати та узагальнити знання учнів про зміст основних понять теми

«Ознаки рівності трикутників»;

- вдосконалити навички розв’язання задач за темою;

- розвивати логічне мислення учнів;

- формувати навички чітко висловлювати думки.

Тип уроку: узагальнення знань та вмінь учнів. 

Методично-дидактичне забезпечення: комп’ютер, презентація PowerPoint, проектор. 

Перебіг уроку 

І. Організаційний момент

У вступному слові педагог формулює тему уроку. Цитує Древньогрецького поета Нівена:

«Математику не можна вивчати 

спостерігаючи, як це робить сусід!» 

(А. Нівен)

Закликає учнів висловити свої думки стосовно цього виразу.

ІІ. Перевірка домашнього завдання 

Математичний диктант (Додаток 1) 

ІІІ. Актуалізація знань. 

Повторення теорем (завершити речення)

Учитель пропонує Завершити речення і записати в зошитах відповідні теореми, підкреслює важливість цих теорем у подальшому виконанні завдань:

1. Трикутники називаються рівними, якщо…. 

2.Якщо дві сторони і …, то такі трикутники рівні. 

3. Якщо сторона і …, то такі трикутники рівні. 

4. Якщо три сторони одного трикутника… , то такі трикутники рівні. 

(слайд 4) 

Знайти відповідність 

(слайд 5) 

Аукціон ідей

Увага! Увага! Сьогодні замість уроку геометрії у нас відбудеться аукціон-розпродаж геометричних фігур.

Що таке аукціон?

Аукціон - це публічний продаж майна, під час якого покупцем стає той, хто запропонує більш високу ціну. Учасники аукціону називаються аукціонерами, людина, яка проводить аукціон, - аукціоністом, а товар - лотом.

На наш аукціон надіслано кілька фігур. 
(слайд 6) 

Умова: хто одразу дає точне означення фігури, той її і купує. Якщо в когось будуть уточнення і доповнення, фігуру буде продано тому, хто закінчить повну відповідь. Отже, намагайтеся одразу дати повну відповідь. Бажаючі відповісти (тобто купити фігуру), піднімають руку. Хто перший підніме - той і починає.

Аукціоніст після кожної неповної відповіді буде бити в гонг до трьох разів, доки не з'явиться учень (аукціонер), який виявить бажання доповнити відповідь.

Зауваження: у випадку, якщо не знайдеться учня, який захоче доповнити, тобто завдання виявиться занадто складним, фігуру доведеться продати попередньому покупцеві. Однак у цьому випадку вчителю доведеться самому доповнити відповідь, щоб не лишати прогалин у знаннях учнів.

У ході продажу фігур (лотів) № 1, 2, 3, 4, 5 доведення рівності трикутників доцільно записувати на дошці, щоб учні ще раз могли простежити відповідність рівних кутів та рівних сторін і пригадати ознаки рівності трикутників. Для цього вчитель може скористатися допомогою помічника - одного з учнів класу. Той самий помічник може допомагати вчителю (аукціоністу) під час проведення аукціону - відзначати, хто перший підвів руку для відповіді. Помічником може бути учень з найнижчим рівнем навчальних досягнень з геометрії, аби, по-перше, залучити і його до процесу, по-друге, надати йому значущості в очах товаришів.

Якщо для відповіді кілька учнів піднімають руку одночасно, треба урізноманітнювати їх виклик, щоб залучити до участі в аукціоні якомога більше школярів.

Усі фігури, що виставляють на продаж, слід зобразити заздалегідь на окремих альбомних аркушах, вирізати з цупкого паперу і розфарбувати.

Аукціон можна розпочинати. 

Розпродаж геометричних фігур і задач

На продаж виставляються трикутники.

1)Продається пара рівних трикутників.

(На слайді зображені два трикутники, що мають дві пари рівних сторін і кути між ними - вертикальні.)

(слайд 7)

Цей лот може придбати той, хто скаже, за якою ознакою трикутники рівні, і, називаючи рівні трикутники, правильно вкаже відповідні вершини

(тобто вимовить: трикутник... дорівнює трикутнику... за двома сторонами і кутом між ними) 

2) Продається пара рівних трикутників.

(На слайді зображені два трикутники, що мають дві пари рівних сторін і одну спільну сторону.)

(слайд 8)

Назвати рівні трикутники і вказати відповідну ознаку

(учень, який відповідає має сказати: трикутник... дорівнює трикутнику... за трьома сторонами). 

3) Продається пара рівних трикутників.

(На слайді зображені два трикутники, що мають пару рівних сторін, спільну сторону і прилеглі до неї рівні внутрішні різносторонні кути.)

(слайд 9)

Назвати рівні трикутники і вказати відповідну ознаку.

(Відповідь. Трикутник... дорівнює трикутнику... за двома сторонами і кутом між ними.) 

4) Продається пара рівних трикутників.

(На слайді зображені два трикутники, що мають спільну сторону і прилеглі до неї дві пари рівних внутрішніх різносторонніх кутів.)

(слайд 10)

Назвати рівні трикутники і вказати відповідну ознаку.

(Відповідь. Трикутник... дорівнює трикутнику... за стороною і прилеглими кутами.) 

5) Продається пара рівних трикутників.

(На слайді зображені два трикутники, що мають пару вертикальних кутів, пару рівних внутрішніх різносторонніх кутів і пару рівних сторін.)

(слайд 11)

Назвати рівні трикутники і вказати відповідну ознаку.

(Очікувана відповідь. Трикутник... дорівнює трикутнику... за стороною і прилеглими кутами.) 

ІV. Виконання письмових вправ 

а) Розв’язування задач із застосуванням ознак рівності трикутників 

(слайд 12) (слайд 13) 

(слайд 14) (слайд 15) 

(слайд 16) (слайд 17) 

(слайд 18) 
б) Виконання вправ за поданими рисунками

За поданими рисунками вам необхідно визначити, за якою ознакою рівні дані трикутники, та знайти невідомі елементи даних трикутників.

(слайд 19) (слайд 20) 

VІ. Це цікаво знати.

Незважаючи на те, що говорять ніби математика суха наука, геометричні фігури ми можемо спостерігати скрізь .

Проходять століття, але роль геометрії в архітектурі не зменшилась. Вона як і раніше залишається її «граматикою». 
Переглянемо декілька фактів, які свідчать про важливе, значне місце математики у повсякденному житті. Розглянемо втілення трикутника як геометричної фігури в архітектурних спорудах, у природі, у писанках. Цікавою є народна уява щодо поширення трикутника на писанках. У ньому втілена ідея триєдності Всесвіту: неба, Землі і води. Цей знак також символізує батька, матір та дитину. Це - символ божественної Трійці. Сяйво у вигляді трикутника - атрибут Бога-Отця.

Рівнобічний трикутник символізує завершеність.

(слайд 21) (слайд 22) 

VІІ. Рефлексія. Оцінювання.

Вчитель ще раз підкреслює важливість даної теми у вивченні геометрії та повсякденні. Відзначає досягнення учнів на уроці. Оцінює їх знання, враховуючи самооцінку.

(слайд 23) 

VІІІ. Домашнє завдання

Записує домашнє завдання на дошці.

§13-16 повтор. № 307,308,310. 

(слайд 24) 

Математичний диктант Додаток 1 

Варіант №1 

1. Яким буде третій кут трикутника, якщо два інших 25⁰ і 45⁰?

а) 45⁰; б) 100⁰; в) 110⁰; г) 90⁰.

2. Один з гострих кутів прямокутного трикутника 42⁰, чому дорівнює інший гострий кут?

а) 48⁰; б) 42⁰; в) 90⁰; г) інша відповідь.

3. В АВС, В=72⁰. Чому дорівнює зовнішній кут трикутника АВС при вершині В?

а) 128⁰; б) 108⁰; в) 98⁰; г) інша відповідь.

4. АВС = КМР, АВ = 7см, ВС = 8см, КР = 11см. Чому відповідно дорівнюють сторони АС, КМ, МР?

а) 7, 8, 11; б) 11, 7, 8; в) 7, 11, 8; г) інша відповідь.

5. У якого трикутника всі сторони рівні?

а) гострокутний; б) прямокутний;

в) рівнобедрений; г) рівносторонній. 

6. Як називається відрізок, що сполучає вершину трикутника серединою протилежної сторони?

а) медіана; б) бісектриса;

в) висота; г) хорда. 

7. За даними малюнка назвіть рівні трикутники, за якою ознакою і чому?

а) В б) А С

С О

А О 

D D В

Прізвище_______________________________клас__________число_________________варіант____

 

1	2	3	4	5	6

7. _________________________________________________________________________________________

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Варіант №2 

1. Яким буде третій кут трикутника, якщо два інших 40⁰ і 35⁰?

а) 75⁰; б) 105⁰; в) 90⁰; г) 115⁰.

2. Один з гострих кутів прямокутного трикутника 37⁰, чому дорівнює інший гострий кут?

а) 43⁰; б) 37⁰; в) 53⁰; г) інша відповідь.

3. В АВС, В=43⁰. Чому дорівнює зовнішній кут трикутника АВС при вершині В?

а) 137⁰; б) 47⁰; в) 127⁰; г) 90⁰.

4. АВС = КМР, АВ = 8см, МР =7см, КР = 11см. Чому відповідно дорівнюють сторони ВС, АС, КМ?

а) 11, 7, 8; б) 8, 7, 11; в) 7, 8, 11; г) 7, 11, 8.

5. У якого трикутника лише дві сторони рівних?

а) гострокутний; б) прямокутний;

в) рівнобедрений; г) рівносторонній. 

6. Як називається відрізок, що сполучає вершину трикутника з протилежною стороною і ділить кут пополам.

а) медіана; б) бісектриса;

в) висота; г) хорда. 

7. За даними малюнка назвіть рівні трикутники, за якою ознакою і чому?

а) В б) В С

D 
 

А С А D 

Прізвище____________________________________клас_________число___________________варіант____ 
 

1	2	3	4	5	6

площу магазину. p> У літературі і телесеріалах обов'язково сюжет зав'язаний на любовному трикутнику.

 

Бермудський трикутник іноді називають ще диявольським трикутником. Це район в Атлантичному океані, в якому відбуваються нібито таємничі зникнення морських і повітряних суден. Район обмежений лініями від Флориди до Бермудських островів, далі до Пуерто-Ріко і назад до Флориди через Багами. Висуваються різні гіпотези для пояснення цих зникнень, від незвичайних погодних явищ до викрадень інопланетянами.

Найбільшу популярність Диявольському трикутнику принесла історія зникнення американського ланки бомбардувальників-торпедоносців. Про це ви можете знайти багато цікавого матеріалу в мережі Internet.

З третьої ознаки рівності трикутників випливає, що трикутник - жорстка фігура.

Уявімо собі дві рейки, у яких два кінці скріплені цвяхом. Така конструкція не є жорсткою: зрушуючи або розсовуючи вільні кінці рейок, ми можемо змінювати кут між ними.

 

Тепер візьмемо ще одну рейку і скріпимо її кінці з вільними кінцями перших двох рейок.

Отримана конструкція - Трикутник - вже буде жорсткою. У ній не можна зрушити або розсунути ніякі дві сторони, тобто не можна змінити ні один кут. Дійсно, якщо Якби це вдалося, то ми отримали б новий трикутник, що не рівний вихідному. Але це неможливо, т. к. новий трикутник повинен бути рівний вихідному по третьому ознакою рівності трикутників. Л.С. Атанасян В«Геометрія 7-9В», стор. 40.

Це властивість - жорсткість трикутника - широко використовується на практиці. Так, щоб закріпити стовп у вертикальному положенні, до нього ставлять підпірку; такий же принцип використовується при установці кронштейна.

Властивість жорсткості трикутника широко використовують у практиці при будівництві залізних конструкцій. 19 березня 2007 Шуховской вежі на Шаболовці виповнилося 85 років.

Трикутники роблять надійними конструкції високовольтних ліній електропередач.

Трикутники у конструкції залізничного моста.

Для складання красивих паркетів використовували трикутники.

Трикутник полярний, трикутник характеристичний. Яких тільки трикутників немає в математиці. У глибоку давнину разом з астрономією з'явилася з'явилася наука - тригонометрія. Слово В«тригонометріяВ» вироблено від грецьких В«трикутникВ» і В«МіряюВ»

Буквальне значення - В«Наука про вимірювання трикутниківВ»

За допомогою натягнутих мотузок завдовжки 3, 4 і 5 одиниць єгипетські жерці отримували прямі кути при зведенні храмів і т.п.

 

Пристрій трикутника Паскаля: кожне число дорівнює сумі двох розташованих над ним чисел. (Обвести трикутником три числа). Все елементарно, але скільки в цьому таїться чудес. Трикутник можна продовжувати необмежено. p> Трикутник Паскаля комп'ютер переклав на мову кольору.

Трикутник Пенроуза або трібар з колекції неможливих об'єктів. Здається, що ми бачимо три бруски квадратного перетину з'єднаних в трикутник. Якщо ви закриєте будь-який кут цієї фігури, то побачите, що всі три бруски з'єднані правильно. Але коли ви приберете руку з закритого кута, то стане очевидним обман. Ті два бруски, які з'єднаються в цьому вугіллі, не повинні бути навіть поблизу один одного!

Для побудови цієї фігури взяли трібар і розбили його на куби. При цьому нічого не змінилося: нова фігура так само абсолютно неможлива, як і попередня їй!

Трикутник Пенроуза надихає художників і скульпторів.

Багато незвичайних фігур ви можете побачити на сайті В«Неможливі об'єктиВ»

 

2. Зараз ми з вами пограємо з мультимедійною дошкою.

Завдання на готових кресленнях: довести рівність трикутників.

Бажають виходять до дошки. Дітей, батьки яких присутні на уроці, опитати обов'язково.

Коментують доказ за планом:

1) назвати рівні елементи трикутників, дати пояснення,

2) назвати рівні елементи трикутників, дати пояснення,

3) назвати рівні елементи трикутників, дати пояснення,

Називають ознака рівності трикутників, формулювання (повну або ключові слова ознаки В«по двох сторонах і куту між нимиВ», В«по стороні і двом прилеглим до неї кутам В»,В« за трьома сторонами В»).

3. Практичні завдання.

Тренажер-гра В«Купи трикутникиВ». p> Електронні тести (1 і 2 варіанти) - аркуші 2,3,4;

кросворд на листі 5, ігрова програма.

Тема: Ознаки рівності трикутників

Мета: узагальнити знання учнів про ознаки рівності трикутників; формувати уміння застосовувати набуті знання в нестандартних ситуаціях для знаходження невідомих величин трикутника; розвивати логічне мислення, просторову уяву. Показати застосування математичних прийомів у астрономії, географії, мореплавстві.

Хід уроку
 

1. 
   Організаційний момент:

Протягом останніх уроків ми працювали над темою «Ознаки рівності трикутників», дали відповіді на питання:

-ЩО розуміють під поняттям « Ознаки рівності трикутників»?

- Як користуватися ознаками при розв'язуванні стандартних вправ?

Сьогодні ми спробуємо дати відповідь на третє питання:
 

• 
  Де можна застосовувати набуті знання?

Тому сьогоднішній урок ми проведемо у вигляді подорожі до країни трикутників.
 

2. 
   Перевірка домашнього завдання:

В історії людства число «3» має велику магічну силу: три бажання, три тополі, три дороги та ін.. . В геометрії число «3» втілює в себе три точки, три відрізки, три кути. Фігурою, що об'єднує ці поняття, є трикутник. Отож, ми збираємося в дорогу до країни трикутників. 

Здавен люди з цікавістю і мрією дивилися на зоряне небо. (Слайд №2) Воно усіяне міріадами зірок і на ньому записана історія Людства і Всесвіту. (Слайд №3,4))Подивіться: ось сузір'я Кассіопеї, Персея, Андромеди. А ось - сузір'я Трикутника. Таке, на перший погляд, просте, і - таке загадкове. Загадкове тому, що в ньому знаходиться туманність М33.(Слайд №5)Подивимося, яку таємницю вона приховує! 

Для цього клас поділимо на три групи: вершина, сторона, кут. В результаті змагання подивимося: який елемент трикутника переможе.

А туманність М33 приховувала запитання командам у вигляді тестів.

(Кожна група сідає за комп'ютером і опрацьовує тести. Оцінка за тест є кількістю балів групі. Результати заносяться до спеціальної таблиці. Тестування проходить за допомогою програми «МОЙ ТЕСТ»).
 

3. 
   Набуття практичних умінь та навичок:

Справа в тому, що існує два сузір'я трикутника. Зараз наша подорож до сузір'я Південного трикутника. (Слайд №6,7).

(Інформація про сузір'я: учнівське повідомлення)

Сузір'я розповіло про себе. А тепер ми надішлемо інформацію, яка допоможе мешканцям Південного трикутника скласти уявлення про нас.

Отже – завдання:

1-а група: За рисунком довести, що < CDF=

2-а група: За рисунком довести, що АС=А₁С₁ (Слайд №9)

3-я група: За рисунком довести, що АС=А₁С₁(Слайд №10)

(Кожна група одержує дані завдання на картках. Після закінчення роботи над завданнями представник кожної групи презентує розв'язок задачі, а члени інших груп контролюють розповідь і аналізують її. Оцінка виставляється у 12- бальній системі і заноситься до таблиці відповідей.)

Справа в тому, що «Трикутники» є не тільки серед сузір'їв. Є вони і на нашій планеті. Наступна наша подорож до трикутника, розташованого в Атлантичному океані. Це – Бермудський трикутник.(Слайд №11).

(Учнівська інформація про Бермудський трикутник).

Берму́дський трику́тник — назва, що зазвичай вживається до території площею 4 тис. км² і утворює на карті трикутник з вершинами у Бермудських островах, Пуерто-Рико і південній Флориді (США). Вважається, що в цих межах за незвичайних обставин зникли декілька суден та літаків. Ще одна зона на протилежному боці планети, «море диявола», поблизу Японії, має схожу репутацію.

Перше повідомлення про зникнення суден при загадкових обставинах належить Є. Джонсону, та опубліковано у 1950 році у статті для «Ассошіейтед прес» (англ. Associated Press). Джонсон, у своїй статті вказав на «загадкові зникнення суден, літаків і човнів у цьому регіоні», якому надав ім'я «море диявола». Повторне повідомлення у пресі, у журналі «Фейт» (англ. Fate), у 1952 році, у статті Джорджа Сенда також описує декілька «дивних морських зникнень». Назву «Бермудський трикутник» популяризував Вінсент Гладіс у своїй статті в 1964 році.

Гідрат метану

Існує думка, що численні родовища гідрату метану на континентальному шельфі можуть бути пов'язані зі зникненнями. У 1981 році американські геологи опубліковали результати досліджень родовища гідрату метану у регіоні Блейк Ридж, розташованому на південний схід від Флориди.

Періодичні викиди газу здатні утворювати бульбашки, розміром з судно, або зони з газованою водою зі щільністю, що не дозволяє утримувати судно на поверхні. Потоплення суден у цьому разі відбувається без будь-яких попередніх підозр. Метан може також «збивати» літаки. Повітря, змішане з ним, має меншу щільність, і у ньому літак швидко втрачає висоту, також в цьому випадку висотомір працює неточно. Окрім того, при достатній концентрації, гідрат метану також може заглушити працюючий двигун.

Велетенські хвилі

Дослідження вказують, що високі хвилі, висотою до 30 метрів, можуть потопити навіть великі судна. Хоч такі хвилі є рідкістю, проте, в деяких місцях, місцеві течії можуть сприяти їх появі.

Північно-Атлантична аномалія

Вважається, що Бермудський трикутник — це район високої електромагнітної активності, впливом якої пояснюють аномальну поведінку електрообладнання та компасів на суднах та літаках.

Завдання для всіх груп: Зафарбована область – область Бермудського трикутника. Точки Х, В, А – острови. 

Завдання: придумати спосіб визначення відстані між островами А, Х, В і «захистити» свій проект.

(Результат оцінюється і заноситься до спеціальної таблиці).

Переходимо до наступного етапу нашої подорожі. «Трикутники» існують і у відносинах між живими істотами, зокрема, людьми. Дві людини можуть домовитися між собою швидко. А чи швидко вони дійдуть згоди, коли з'являється третя?

4. 
   Самостійна робота для всіх груп:

(Після виконання – роботи перевіряються члени інших груп і виставляють оцінки. Якщо результати перевірки спірні – то результати аналізуються всім класом.)

• 
  1 варіант: 1. Два кути трикутника дорівнюють 35° і 68°. Знайти третій кут.
  • 
    2. Периметр трикутника 35см. Знайти довжину його сторін, якщо одна з них довша за другу на 3 см і коротша за третю на 5 см.

• 
  2 варіант: 1. Два кути трикутника дорівнюють 87° і 56°. Знайти третій кут.

• 
  2. Периметр трикутника 62 см. Знайти довжину його сторін, якщо одна з них довша за другу в 2 рази, а за третю – на 8 см.

• 
  3 варіант: 1. Два кути трикутника рівні 130° і 25°. Знайти третій кут.

• 
  2. Периметр трикутника 85м. Знайти довжину його сторін , якщо одна з них коротша за другу в 2 рази, а за третю – на 1м.

5. 
   Підсумки уроку: за кількістю набраних балів визначається група-переможець, а також виставляються оцінки в індивідуальному порядку.
6. 
   Домашнє завдання: ст..103, № 2,6,8. Підготуватися до к/р.

Автор: вчитель математики Ригун Людмила Вікторівна

Мета уроку: узагальнити і систематизувати знання учнів про трикутники; закріпити знання та навички використання теоретичних знань до розв’язування задач. Розвивати інтерес до навчання , пам’ять , просторову уяву, креслярські навички. Виховувати свідоме ставлення до навчання , старанність , самостійність.

Тип уроку. Урок узагальнення та систематизації знань, умінь і навичок.

Обладнання : моделі різних видів трикутників, таблиці до розв’язування задач за готовими малюнками, слайди.

Епіграф до уроку : «У величезному саду геометрії кожний може підібрати собі букет за смаком.»

Д. Гільберт

Хід уроку

І. Організаційний момент.

ІІ. Мотивація навчальної діяльності.

На початку уроку дітям роздано аркуші настрою . На ньому учні позначають , який настрій був у них на початку уроку і який – у кінці. Так з′ясовую думку школярів про якість уроку.

Діти, а чи знаєте ви де в нашому житті використовують знання про трикутники ? Їх рівність ? Пропоную вам переглянути пізнавальні мультфільми «Трикутники» , та «Розумна цибулинка. Трикутники навколо нас. ( Демонстрація мультфільмів)

Ви , мабуть зрозуміли , що мова на уроці піде про « його Величність Трикутник». Сьогодні ми з вами здійснимо подорож до Країни Рівних Трикутників. Перепусткою до неї будуть правильні відповіді на запитання

 

ІІ. Актуалізація опорних знань.

Зупинка «Розминка»

Сформулюйте першу, другу та третю ознаки рівності трикутників.

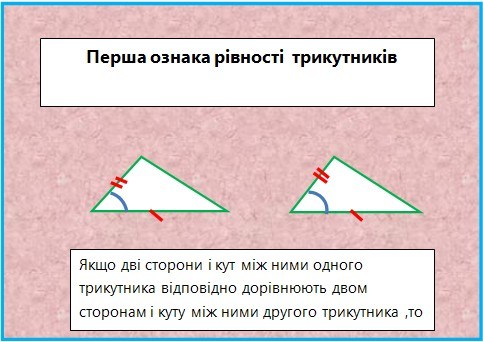
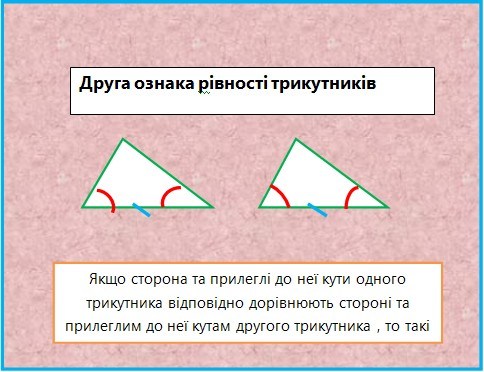
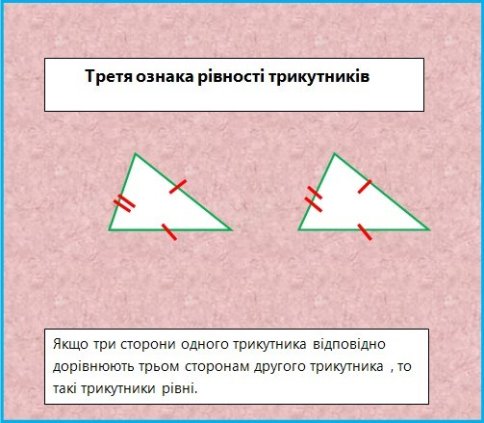
ІІІ. Закріплення умінь та навичок.

Задача №1

Які ще елементи ,крім позначених на рисунку , повинні бути рівними , щоб довести рівність трикутників за першою ознакою їх рівності?

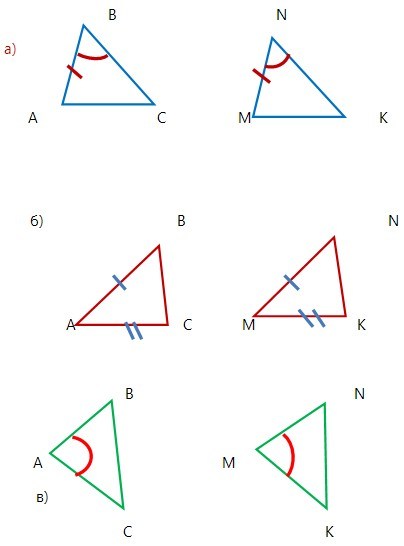
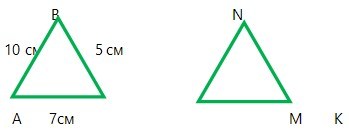
Задача №2

Яку рівність необхідно додати у трикутниках АВС і МNК , щоб довести їх рівність за другою ознакою ?

 

Зупинка « Поспіши , розв’яжи»                             

Задача №3

Чи рівні ці трикутники?

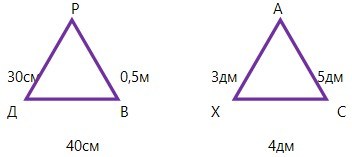
Завдання №4

Доведіть рівність трикутників АВС і А₁В₁С₁ і знайдіть периметр трикутника АВС.

Зупинка «Індивідуальна»

Завдання №5

На рисунку кут ВАС дорівнює куту ДАС, АВ = АД. Довести рівність трикутників АВС і АДС.

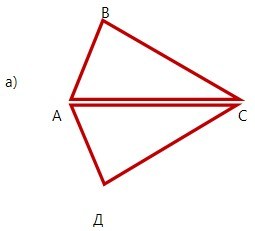
На рисунку ВО = ДО, кут ОВС дорівнює куту ОДА. Довести рівність трикутників ОВС та ОДА.

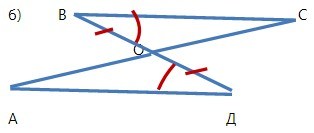
Задача № 6

Закінчіть речення : « Перша ознака рівності трикутників – це ознака рівності за …»

« Друга ознака рівності трикутників – це ознака рівності за …»

«Третя ознака рівності трикутників – це ознака рівності за …»

Завдання №7

Знайдіть сторони трикутника МNК , якщо Δ АВС = ΔМNК .

Задача №8

Чи можуть три кути трикутника бути прямими ? Чому?

Зупинка « Художник»

Задача №9

У трикутнику АВС АС = 5см , кут А дорівнює 60⁰,кут С дорівнює 45⁰. Побудуйте ΔА₁В₁С₁ = ΔАВС.

Зупинка «Логічна»

Задача № 10

Яку схему міркувань ви склали б для розв’язування задачі?

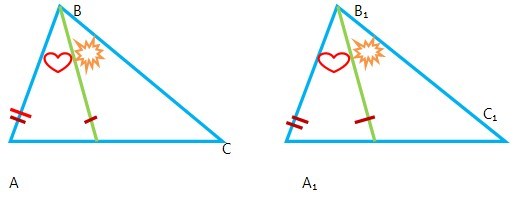
Доведіть : ВС = В₁С₁.

Задача № 11

Відрізок СД перпендикулярний до відрізка АВ і проходить через його середину. Доведіть рівність трикутників АСД і ВСД.

Задача №12

Доведіть рівність рівнобедрених трикутників за основою та периметром.

Задача № 13

Один з моїх гострих кутів дорівнює 45⁰. Що про мене можна сказати , якщо я прямокутний ?

Зупинка « Ігротека»

Задача № 17

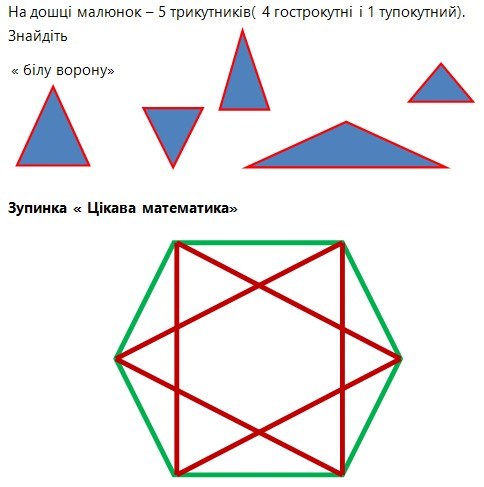
Скільки трикутників на малюнку ? Відповідь : 32

IV. Підсумок уроку.

Дякуємо всім , що завітали на урок і брали в ньому активну участь. Всі ви сьогодні отримуєте білети до Країни Рівних Трикутників. Родина цих фігур велика, дружна. Зустрінемося з нею ще не раз. Аркуші настрою зібрано з коментуванням.

Бажаю всім присутнім

Я успіхів,удачі !

Приходьте на уроки,

Розв′язуйте задачі!

Жартівливий епілог : « Дерево розуму виростає із шишок на лобі».

V. Домашнє завдання. Спробуйте розрізати рівносторонній трикутник на 5 рівнобедрених. Виконайте практично.

Подобається