Розв'язування задач з теми «Подібність три¬кутників».

Тема. Розв'язування задач з теми «Подібність три­кутників».

Мета: узагальнити, систематизувати знання учнів про зміст та схе­ми застосування означення та ознак подібності трикутників. Відпрацю­вати навички застосування набутих знань. Провести діагностику рів­ня засвоєння учнями навчального матеріалу з теми «Подібність три­кутників».

Тип уроку: комбінований.

Наочність та обладнання: конспект «Подібність трикутників».

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

З метою фронтальної перевірки засвоєння учнями змісту ознак подібності трикутників проводиться математичний диктант.

Математичний диктант

Також на уроці слід перевірити розв'язання додаткової задачі (пов­не розв'язання цієї задачі записує на дошці один з учнів заздалегідь; учні знайомляться з його змістом після виконання та перевірки завдань математичного диктанту).

III. Формулювання мети і завдань уроку

На цьому етапі уроку доречними будуть слова вчителя про те, що на попередніх трьох уроках учні окремо вивчали ознаки подібності трикутників та способи їх застосування, причому кожного уроку учні розв'язували задачі на застосування лише тієї ознаки, яка вивчалась на уроці, тобто учні працювали в «штучних умовах», за відсутності пробле­ми вибору, коли заздалегідь було відомо, який набір елементів трикут­ників (зумовлений певною ознакою подібності) слід виділити в даних трикутниках для доведення їх подібності саме за певною ознакою.

Вчителю слід наголосити на тому, що на практиці під час розв'язування задач, які передбачають застосування ознак подібності трикутників, вибір певної ознаки слід робити самому учневі, виходячи з умови задачі та своїх знань. Тому для успішного розв'язування задач на подібність трикутників учням, крім сталих знань змісту окремих оз­нак подібності трикутників та наслідків із них, слід оволодіти вміння­ми вибирати ознаку чи наслідок відповідно до умови задачі.

Отже, мета уроку — закріплення та систематизація знань учнів про ознаки подібності трикутників та відпрацювання навичок їх вико­ристання під час розв'язування задач на подібність трикутників.

IV. Актуалізація та систематизація опорних знань

Усвідомлення, повторення та систематизація знань учнів про зміст означення та ознак подібності трикутників можна провести в такій формі: до уваги учнів пропонується рис, за яким вони виконують завдання — до кожного з рисунків скласти відповідне твердження (означення чи якусь із ознак подібності трикутників). Для того, щоб залучити до роботи якомога більше учнів, можна організувати роботу в малих Трупах. У такому разі спочатку завдання виконується в групах, а потім результати виконання завдання презентуються та коригуються.

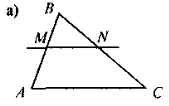
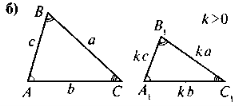
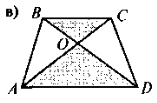
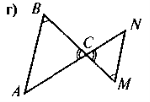
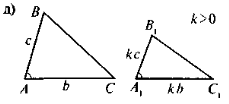
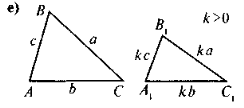
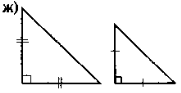
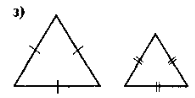
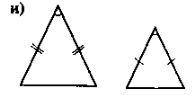
Рис.

V. Відпрацювання навичок

Застосування знань у стандартних ситуаціях

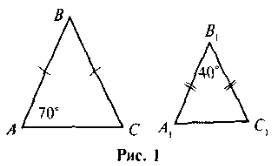
1. За даними рис. 1 доведіть, що ΔАВС ~ ΔА₁В₁С₁.

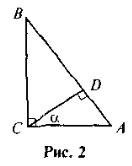
2. Нарис. 2 знайдіть трикутники, подібні до трикутника ABC, і до­
   ведіть їхню подібність.
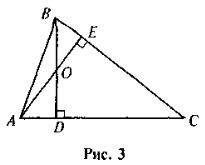
3. Знайдіть на рис. 3 всі пари подібних трикутників і доведіть їхню
   подібність.

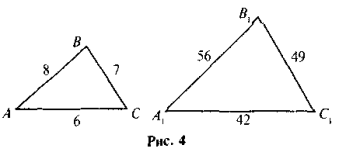
4. За даними рис. 4 доведіть, що ΔАВС ~ ΔА₁В₁С₁.
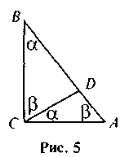
5. На рис. 5 знайдіть трикутники, подібні до трикутника ABC, і до­ведіть їхню подібність.

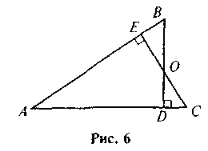
6. На рис. 6 знайдіть усі пари подібних трикутників і доведіть їхню
   подібність.

Застосування знань у нестандартних ситуаціях

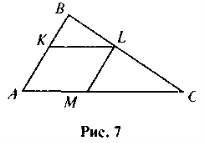
1. У трикутник ABC вписано ромб AKLM (рис 7) Знайдіть периметр ромба, якщо ВК = 4 см,    МС = 9 см.
2. Діагоналі трапеції точкою перетину діляться у відношенні 3 : 7. Знайдіть основи трапеції, якщо її середня ліня дорівнює 10см

VI. Діагностика знань та вмінь

Учням пропонується самостійно розв'язати завдання як на знання і розуміння ознак подібності трикутників, так і на застосування цих знань у комплексі із набутими раніше знаннями

Самостійне розв'язування задач

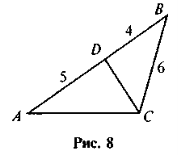
1. Знайдіть нарис  8подібні трикутники і доведіть їхню подібність.

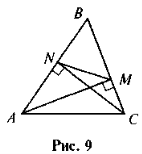
2. За даними рис 9 доведіть, що ΔАВС ~ ΔMBN.
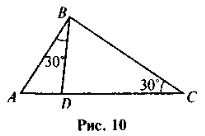
3. Знайдіть на рис 10 подібні трикутники і доведіть їхню подібність.

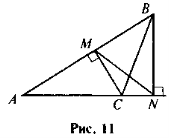
4. За даними рис 11 доведіть, що ΔABC ~ ΔANM.
5. Точка перетину діагоналей трапеції ділить одну з них на відрізки завдовжки 5 см і 9 см Знайдіть основи трапеції, якщо їх сума дорів­нює   70 см.
6. Основи трапеції дорівнюють 7 см і 15 см Знайдіть відрізки діаго­налі, на які її ділить друга діагональ, якщо різниця цих відрізків дорівнює 24 см.

VII. Підсумки уроку

По закінченні виконання самостійних завдань проводиться перевірка правильності виконання, таким чином встановлюється, чи досягнута мста уроку; в учнів з'являються підстави для самооцінки та усвідомлення своїх недоліків, над якими слід працювати.

VIII. Домашнє завдання

Повторити зміст: означення, ознаки подібності трикутників та опорні факти для доведення подібності трикутників; зміст поняття перпендикуляра до прямої; означення та властивості прямокутного трикутника.

Розв'язати задачі.

1. У рівнобедреному трикутнику ABC з основою АС кут В дорівнює 36°, AD — бісектриса трикутника. Доведіть, що ΔАВС ~ ΔCAD.
2. Одна з діагоналей трапеції дорівнює 28 см і ділить другу діагональ на відрізки довжиною 5 см і 9 см. Знаючи, що менша основа тра­пеції дорівнює 6 см, знайдіть:

а) відрізки, на які точка перетину діагоналей ділить першу діагональ;

б) бічну основу трапеції.

3. У трикутник ABC вписано ромб АКРЕ так, що кут А спільний, а вершина Р належить стороні ВС. Знайдіть сторону ромба, якщо
   АВ = 6 см, АС = 3 см.