Перпендикуляр і похила. Розв'язування задач
Тема. Перпендикуляр і похила. Розв'язування задач
Мета: сформувати в учнів свідоме розуміння змісту понять похилої до прямої, проекції похилої на пряму, а також властивостей перпендикуляра, похилих та їх проекцій.
Сформувати вміння:
- відтворювати зміст вивчених понять;
- знаходити названі геометричні об'єкти на рисунку;
- виконувати рисунок із зображенням названих об'єктів за даним описом;
- застосовувати формулювання властивостей перпендикулярів, похилих та проекцій для розв'язування задач.
Тип уроку: застосування знань, умінь та навичок.
Наочність та обладнання: конспект «Перпендикуляр і похила».
Хід уроку
І. Організаційний етап
II. Перевірка домашнього завдання
Математичний диктант
|
|
Варіант 1 |
Варіант 2 |
|
1 |
Закінчіть речення: Якщо квадрат сторони трикутника дорівнює сумі квадратів двох його інших сторін, то... |
У ΔMNK MN2 = МК2 + NK2. Знайдіть градусну міру найбільшого кута ΔММК |
|
2 |
У ΔSTO ST2 + ТО2 = SO2. Яка градусна міра найбільшого кута ΔSTO? |
Заповніть пропуски: Якщо квадрат сторони... дорівнює сумі квадратів двох інших сторін..., то кут... прямий |
|
3 |
Визначте, чи є в трикутнику прямий кут, якщо його сторони |
|
|
|
40 см, 41 см, 9 cm |
25 см, 24 см, 27 см |
|
4 |
Діагоналі паралелограма мають довжину 6 см і 8 см, а одна зі сторін — 5 см. Що можна сказати про цей паралелограм? |
Відомо, що довжина сторін паралелограма 5 см і 12 см, а одна з діагоналей має довжину 13 см. Що можна сказати про цей паралелограм? |
III. Формулювання мети і завдань уроку
Учитель повідомляє проте, що в математиці існують поняття, властивості яких мають пряме відношення до теореми Піфагора. На уроці відбудеться ознайомлення учнів з цими поняттями, а також будуть досліджені їх властивості, що випливають із тверджень теореми Піфагора.
IV. Актуалізація опорних знань
З метою успішного засвоєння учнями змісту поняття похилої до прямої, проекції похилої на пряму, а також розуміння учнями їх властивостей, слід активізувати знання і вміння щодо означення перпендикуляра, проведеного з точки поза прямою, та його властивостей: означення Прямокутного трикутника та властивостей його сторін; теореми Піфагора.
 Виконання усних вправ
Виконання усних вправ
- Два креслярські трикутники розміщені так. як показано на рис. 1. Що можна сказати з цього приводу?
- Чи може діагональ прямокутника бути меншою за одну з його сторін?
-
Чи може діагональ ромба бути в два рази
довшою за його сторону? - У теоремі Піфагора назвіть умову і висновок.
V. Засвоєння знань
План вивчення нового матеріалу
- Похила, проведена з точки до прямої; основа перпендикуляра та основа похилої; проекція похилої на пряму.
- Властивості перпендикуляра, похилих та їх проекцій.
|
Конспект 14 |
||
|
Перпендикуляр і похила |
||
|
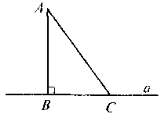
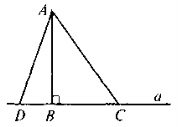
Відрізок АВ — перпендикуляр до прямої а; відрізок АС — похила до прямої; відрізок ВС — проекція похилої АС на пряму а . |
||
|
|
||
|
Властивості
Якщо АВ 1) АС > АВ; АС > ВС;
2) АС = AD
3) AC > AD |
|
|
|
Якщо перпендикуляр і похила проведені з однієї точки до однієї прямої, то |
||
|
будь-яка похила більша за перпендикуляр і за свою проекцію |
Рівні похилі мають рівні проекції, і навпаки |
більша похила має більшу проекцію, і навпаки |
VI. Формування первинних умінь
Засвоєння змісту понять «похила...» та їх властивостей відбувається у процесі розв'язування усних задач.
Виконання усних вправ
- Із точки поза прямою проведено до неї дві похилі, одна з яких має довжину 10 см і утворює зі своєю проекцією на пряму кут 30°. Знайдіть довжину другої похилої, якщо вона утворює з прямою кут 45°.
-
У трикутнику ABC
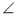 1 = 90°. Назвіть:
1 = 90°. Назвіть:
а) похилу до прямої АВ , проведену з точки С;
б) проекцію похилої ВС на пряму АС .
- Відрізки о, і а2 — проекції похилих l1 і l2, проведених з однієї точки до однієї прямої. Порівняйте:
а) l1 і l2, якщо а1 < а2;
б) а1 і а2, якщо l1 = l2.
- Дві похилі до однієї прямої мають рівні проекції. Чи обов'язково ці похилі рівні?
-
Скільки рівних похилих до даної прямої можна провести з точки,
яка не лежить на цій прямій?
Під час розв'язування задач бажано виконувати відповідні ілюстрації.
- Сформулюйте теорему Піфагора, використовуючи поняття «перпендикуляр», «похила», «проекція похилої».
Виконання графічних вправ
-
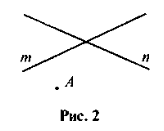 Дано прямі т і п, точку А поза ними (див. рис. 2). Проведіть перпендикуляри з даної точки до даних прямих. Із даної точки проведіть по дві похилі до кожної з прямих. Виконайте записи властивостей перпендикуляра, похилих та їх проекцій на відрізки, що утворилися на вашому рисунку, виконавши необхідні вимірювання.
Дано прямі т і п, точку А поза ними (див. рис. 2). Проведіть перпендикуляри з даної точки до даних прямих. Із даної точки проведіть по дві похилі до кожної з прямих. Виконайте записи властивостей перпендикуляра, похилих та їх проекцій на відрізки, що утворилися на вашому рисунку, виконавши необхідні вимірювання.
-
Із точки, що лежить на відстані 4 см від даної прямої, треба про
вести дві похилі довжиною 5 см і 6 см. Як виконати цю побудову?
Скількома способами це можна зробити?
Виконання письмових вправ
- Із точки, взятої на відстані 12 см від прямої, проведено до неї дві похилі. Знайдіть відстань між основами похилих, якщо їх сума дорівнює 28 см, а проекції похилих відносяться як 5 : 9.
- Із однієї точки до даної прямої проведено дві рівні похилі. Відстань між їх основами 14 см. Визначте проекції похилих на дану пряму.
- Точка знаходиться на відстані 6 см від прямої. З неї до прямої проведено похилу, яка утворює з прямою кут 45°. Знайдіть проекцію похилої на цю пряму.
- Із точки поза прямою проведено до неї дві похилі; довжина однієї з них дорівнює 25 см, а довжина її проекції — 15 см. Знайдіть довжину другої похилої, якщо вона утворює з прямою кут 30°.
- Із точки до прямої проведено перпендикуляр завдовжки 8 см і дві похилі з довжинами 10 см і 17 см. Знайдіть відстань між основами похилих. Скільки розв'язків має задача?
- Знайдіть висоту, проведену до найбільшої сторони трикутника зі сторонами 15, 41 і 52.
VII. Підсумки уроку
Тестове завдання
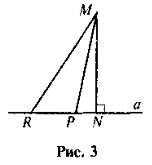
- Нехай MN — перпендикуляр, опущений із точки М на пряму а, а Р і R — будь-які точки прямої а (рис. 3). Яке твердження неправильне?
1) Відрізки MP і MR називаються похилими, проведеними з точки М до прямої а.
2) PN і RN — проекція похилих MP і MR.
3) Якщо PN < NR, то MP < MR.
4) З даної точки поза прямою можна провести до неї три похилі однакової довжини.
-
Похила довжиною 10 см, проведена з даної точки до прямої, має
проекцію довжиною 6 см. Обчисліть довжину перпендикуляра,
опущеного з тієї самої точки на пряму.
1) 9 см; 2) 8 см; 3) 7 см; 4) 6 см.
- Із точки К до прямої а проведено перпендикуляр і похилу довжиною відповідно 15 см і 17 см. Знайдіть проекцію похилої.
1) 6 см; 2) 7 см; 3) 8 см; 4) 9 см.
-
У трикутнику ABC
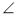 C = 90°, CD
C = 90°, CD 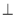 AB, AC = 13 см, CD = 5 см, AB = 20 см (рис. 4). Знайдіть проекцію катета СВ на гіпотенузу АВ.
AB, AC = 13 см, CD = 5 см, AB = 20 см (рис. 4). Знайдіть проекцію катета СВ на гіпотенузу АВ.
1) 5 см; 2) 6 см; 3) 7 см; 4) 8 см.
- Відрізок MN дорівнює 25 см. Його кінці лежать від прямої а на відстані 4 см і 11 см. Знайдіть проекцію відрізка MN на цю пряму.
1) 22 см; 2) 23 см; 3) 24 см; 4) 20 см.
VIII. Домашнє завдання
Вивчити зміст основних понять уроку.
Розв'язати задачі.
- З точки до прямої проведено перпендикуляр і похилу. Знайдіть довжину:
а) похилої, якщо її проекція дорівнює 9 см, а перпендикуляр має довжину 40 см;
б) перпендикуляра, якщо похила та її проекція дорівнюють відповідно 29 см і 20 см.
-
Знайдіть висоту, проведену до найбільшої сторони трикутника зі
сторонами 15, 13 і 14. - із точки до прямої проведено перпендикуляр і дві похилі, різниця довжин яких складає 8 см. Знайдіть довжину перпендикуляра, якщо проекції похилих дорівнюють 8 см і 20 см.
Повторити ознаки подібності прямокутних трикутників, означення бісектриси трикутника, властивість бісектриси рівнобедреного
трикутника, проведеної до основи.


про публікацію авторської розробки
Додати розробку