Розв'язування задач з теми "Вектори та дії над координатами векторів"

Тема уроку: Розв’язування задач. Самостійна робота

Мета уроку:

• систематично стежити за грамотністю висловлювання учнів рідною мовою, доречним та коректним вживанням у мовленні математичної термінології;
• оперувати числовою інформацією, геометричними об’єктами в просторі;
• розвивати здатність концентруватися, передбачати результативність;

 

Тип уроку: повторення і систематизація знань

Наочність та обладнання:

Очікувані результати.

Учень/учениця:

Після закінчення уроку учень/учениця:

• знає: теоретичний матеріал
• вміє: оперувати з векторами
• може: застосувати вивчений теоретичний матеріал до розв’язування задач

Хід уроку

 

І. Організаційний момент.

 На початку уроку учні оцінюють власне почуття впевненості у знаннях за шкалою.  

                  1  -  10  -  20  -  30  -  40  -  50  -  60  -  70  -  80  -  90  -  100                 

     зовсім не впевнений                                                          абсолютно впевнений         

Епіграф до уроку:

Добре засвоєна мудрість не забувається ніколи

 Піфагор

ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

 Чи є у вас запитання по домашньому завданні? Чи є сьогодні на уроці такі учні, які не зуміли справитися із домашнім завданням? Прошу консультантів доповісти про виконання учнями д/з.

ІІІ. ФОРМУЛЮВАННЯ ТЕМИ, МЕТИ І ЗАВДАНЬ УРОКУ

Метою нашого сьогоднішнього уроку є: систематизація знань, умінь і навичок з вивченого на попередніх уроках.

ІV. Актуалізація опорних знань і вмінь.

1. Актуалізація проводиться  з допомогою презентації «Вектори в просторі», підготовленої учнями.

1.Означення вектора.

2.Абсолютна величина вектора.

3.Рівні вектори.

4.Формула довжини вектора.

5.Дії з векторами.

6.Колінеарні вектори.

7.Перпендикулярні вектори

 

2. Виконання усних вправ

1.Знайдіть координати вектора , якщо М(10;-4;2), К(16;2;-5).

   ( відповідь (6;6;-7)).

2. Чи правильно, що вектори  (-5;-4;-3), (3;4;5)   рівні?   (відповідь ні).

3. Знайдіть координати вектора 2, якщо (1;-4;0).    (відповідь  (2;-8;0) ).

4. Знайдіть модуль вектора (-3;-3;-3). (відповідь 3).

 5. Чи колінеарні вектори (1;-3;2) і (3;-9;6)? (відповідь так).

6. Чи перпендикулярні вектори (випереджуюче завдання) (-5; 0 ;3), (3;4;5)? (відповідь так)

 

V. Усвідомлення вивченого матеріалу

Колективне розв’язування вправ.

1. При якому значенні р вектори (4;2р-1;-1), (4;7;-1) рівні  ? (р=4).

 2. Знайти модуль вектора 2-3, якщо (2;0;-3), (1;-1;-4) . ().

VI. Закріплення та перевірка знань, вмінь і навичок

Варіант 1

Початковий рівень навчальних досягнень

1. Якщо А(-2;4;1), В(3;-7;1), то координати вектора  …

а)  ;                                        б);

в)   ;                                       г) .               

2. Абсолютна величина вектора дорівнює …

а) 1;            б) 5;            в) 3;                г)-1.

3. Який вектор колінеарний вектору ?

а) ;      б) ;        в) ;   г) .

 

Середній рівень навчальних досягнень

4. Координати вектора , якщо дорівнюють …

а) ;      б) ;      в) ;      г) .

5. Який вектор дорівнює сумі векторів і ?

а) ;      б) ;        в) ;      г) .

6. При якому значенні m вектори і рівні , якщо , , , ?

Достатній та високий рівні  навчальних досягнень

7.  Дано вектори і . Знайти абсолютну величину вектора .

8. При яких значеннях n вектори і перпендикулярні?

9. При яких значеннях y і z  вектори і колінеарні?

 

 Варіант 2

Початковий рівень навчальних досягнень

1. Якщо А(3;-5;2), В(4;-9;2), то координати вектора  …

а)  ;                                        б);

в)   ;                                       г) .               

2. Абсолютна величина вектора дорівнює …

а) 1;            б) 5;            в) 3;                г)-1.

3. Який вектор колінеарний вектору ?

а) ;      б) ;        в) ;   г) .

 

Середній  рівень навчальних досягнень

4. Координати вектора , якщо дорівнюють …

а);      б);      в);        г).

5. Який вектор дорівнює різниці векторів і ?

а) ;     б) ;    в) ;     г).

6. При якому значенні а  вектори    і    перпендикулярні , якщо   і ?

  а)1;                 б) 2;                  в) -3;               г) 0.   

 

Достатній та високий рівні  навчальних досягнень

 

7.  Дано вектори і . Знайти абсолютну величину вектора .

8. При яких значеннях n  скалярний добуток векторів і дорівнює 6?

9. При яких значеннях x і y вектори і колінеарні?

 

Відповіді.

Варіант 1.

1-в;  2-в;  3-а;  4-б;  5-в;  6.1;  7. 3;  8. -;  9. .

Варіант 2.

1-г;  2-б;  3-в;  4-б; 5-г;  6-а;  7. ;  8. ; 9. .

 

VII. Домашнє завдання:

повторити§3.3; §3.4

виконати

домашню  роботу:

1. Знайти довжину вектора 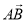, якщо А(4;1;-3), В(2;-1;-3).
2. Знайти скалярний добуток векторів 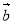(2;-4;3) і 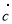(-1;0;2).
3. Знайти модуль вектора 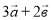 , якщо 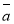(1;0;-2), 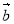(2;-2;1).
4. Знайти значення р, при якому вектори 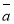(р;3;-1) і 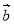(2;р;-5) перпендикулярні.
5. Знайти суму, різницю та їх абсолютну величину векторів 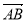і 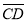, якщо А(1;-1;0), В(3;1;-2), С(-1;0;2), Д(0;1;3).

 

VIIІ. Підсумки уроку.

IX. Рефлексія (осмислення результатів уроку)

      Рефлексія діяльності на уроці.

Людина здорова, наділена мудрістю, що володіє запасом знань відчуває себе впевнено, гідно, вона може багато що в житті зробити. Дорогі діти, цінуйте, поважайте і бережіть своє здоров’я, здоров’я своїх близьких, це найдорожче багатство, яке не терпить зневажливого відношення до себе. Наприкінці уроку давайте знімемо напругу і втому, згадаємо, що ми частина природи.

Що сприяло успіху?  Що заважало?

Оцінити результативність своєї роботи на уроці за 100-бальною шкалою.

                  1  -  10  -  20  -  30  -  40  -  50  -  60  -  70  -  80  -  90  -  100                 

     зовсім не впевнений                                                          абсолютно впевнений         

  В кінці уроку треба порівняти очікування з результатом.    В чому причина невдач?   

Урок завершено. Бувайте здорові.