Розв’зування задач за допомогою рівнянь

Урок математики у 6 класі

Автор статті пропонує розробку уроку для учнів 6-х класів, на якому використовує різноманітні форми роботи. Акцент поставлено на методику складання рівнянь за умовою задачі.

Ірина КИРДЕЙ, учитель математики Білоцерківської СПМШ І-ІІІ ст. № 16, Київська обл.

 

Без знання дробів ніхто не може визнавати, що знає математику.

Цицерон

Тема: Розв’зування задач за допомогою рівнянь

 

Мета:  навчальна: узагальнити та систематизувати знання учнів щодо розв’язування рівнянь;

розвивальна:розвивати логічне мислення учнів, увагу, пам'ять; формувати пізнавальну компетентність прищеплювати любов до математики, вчити розв’язувати задачі тестового характеру;  виховна: виховувати працьовитість, активність, самостійність, впевненість у собі.

тип уроку: формування знань, умінь і навичок форма проведення: довільна (дистанційна або очна) 

 

 

Перебіг уроку:

Пригадаймо, що…
Знайти частину від числа – помножити число на відповідний дріб.	Знайти ціле, знаючи його частину – поділити частину на відповідний дріб.
Властивості рівнянь Доданки можна переносити з однієї частини рівняння  іншу, змінивши при цьому їх знаки на протилежні.	Властивості рівнянь Обидві частини рівняння можна одночасно множити або ділити на одне і теж число (не 0).
Розкриття дужок (стрілочки) a(b + c) = ab + ac;   a(b - c) = ab - ac;	Розкриття дужок m + (k - r) = m + k - r ;   m - (k - r) = m - k + r ;
Задачі І типу   РАЗОМ   + додавання	Задачі ІІ типу -         більше/менше -         коротше/довше -         важче/легше -         віднімання
Середнє арифметичне – це сума чисел, поділена на їх кількість.	На 5 більше: х+5; У 5 разів більше: 5х.
І. Організаційна частина.  (Привітання, організація учнів на роботу в класі).

ІІ. Перевірка домашнього завдання, заданого напередодні Завдання 1. Знайди середнє арифметичне чисел: 24,8; 156; 78,3; 62,5.

Розв’язання. 24,815678,362,5  321,6  80,4.

                                                             4                          4

Завдання 2. Розв’яжи рівняння:

а) 3х+18х-14х-22,43 = 40,85; х(3+18-14)=40,85 + 22,43; 7х = 63,28; х=9,04.

б) 3,67(5у-13)=29,36 | ·100 367(5у-13)=2936; 5у-13 = 2936:367; 5у-13 = 8; 5у=21; у= 21:5; у=4,2.

 

Задача 3. На вівторок з математики було задано  кількості задач, заданих на понеділок. Скільки задач було задано на понеділок і скільки на вівторок, якщо за два дні потрібно було розв’язати 46 задач?

Розв’язання. 

На понеділок – х задач;

На вівторок –   х задач. Рівняння: х+   х = 46; х(1 +  ) = 46;  х = 46 |:23

х

=2; 14 х=28.

Методичний коментар. Учитель акцентує увагу на значному спрощенні розв’язування рівняння завдяки використанню властивостей рівнянь.

Отже, на понеділок було задано 28 задач, а на вівторок 46-28 = 18 задач.

Відповідь. 28 задач і 18 задач.

Задача 4. Арсеній, Борис, Валентина і Ганна збирали лікарські рослини і в кінці дня виявилось, що в середньому вони зібрали по 1,8 кг. Скільки кг лікарських рослин зібрав кожен із них, якщо відомо, що Ганна зібрала на 200 г більше, ніж Валентина; Валентина – на 200 г більше, ніж Борис; Борис – на 200 г більше, ніж Арсеній?

Розв’язання. 200 г = 0,2 кг.

Арсеній – х кг

Борис – х+0,2 кг

Валентина – х+0,2+0,2 = х+0,4 кг;

Ганна – х+0,2 +0,2 +0,2 = х+0,6 кг.

Рівняння: (х+х+0,2 +х+0,4+х+0,6):4 = 1,8;

4х+1,2 = 7,2; 4х = 7,2-1,2; 4х=6; х=6:4; х=1,5. 

Отже, Арсеній зібрав 1,5 кг лікарських рослин, Борис – 1,5+0,2 = 1,7 кг, Валентина 1,7+0,2=1,9 кг, Ганна 1,9+0,2=2,1 кг.

Відповідь. 1,5 кг; 1,7 кг; 1,9 кг; 2,1 кг.

Перевірка. 1,5  1,7 1,9  2,1  7,2 1,8.

                                                 4                     4

Задача 5. У неділю Андрій полив 36 дерев. Це 12% наявних дерев у парку. Скільки дерев росте в парку?

Розв’язання. 36 дерев – це 12%=0,12

                      Всі дерева – це 100%. Отже, потрібно знайти число, знаючи його частину:

36 : 0,12 = 3600: 12 = 300 (дерев) – в парку всього. Відповідь. 300 дерев. 

Задача 6 (додаткова). Знайди таке значення для букви а, при якому коренем рівняння буде число -2:

(6а+1)х = -5а+4х – 8.

Розв’язання. Корінь рівняння – це значення букви х, отже, х=-2. Підставимо х=-2 в рівняння:

(6а+1)· (-2) = -5а + 4 ·(-2) – 8;

-12а-2 = -5а-8-8;

-12а+5а = -16+2;

-7а=-14; а=-14 : (-7); а=2.

Відповідь. Коли а=2, то х=-2.

 

ІІІ. Розв*язування задач № 1382 – 1385 (підручник «Математика, 6 клас», авт. Істер О.С.).

Зразки для запису розв’язування задачі в зошиті.

 

Розв’язання.  90% = 0,9.

І хлопчик – х наклейок;

ІІ хлопчик – 0,9х наклейок.

Рівняння: х+0,9х = 380; 1,9х=380; х=380:1,9; х= 200.

Отже, у І хлопчика 200 наклейок, тоді у другого 380-200=180 наклейок.

Відповідь. 200 і 180 наклейок.

 

Розв’язання. 

І самоскид – х тонн

ІІ самоскид – 3 х тонн

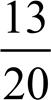
x1= 3x

                                                             

                                                                              

                                         13            3

                             x1  3x ;

                                         20            4

113   53       3x x; 128  17 12; x 65; Рівняння: 20         4             20 5     5 

                            1 2x;                                               x1,2.

Отже, на І самоскиді 1,2 тонни вантажу, а на другому - 3·1,2 = 3,6 тонни.

Відповідь. 1,2 т і 3,6 т.

Задача. За 8 однакових ручок і 5 однакових блокнотів заплатили 305  грн. Скільки коштує одна ручка і один блокнот, якщо відомо, що блокнот дорожчих за ручку на 9 грн.?

Розв’язання.

Ручка – х грн.;

Блокнот – х+9 грн.

Рівняння: 8х + 5(х+9)=305;

8х+5х+45=305; 13х=305-45; 13х=260; х=20.

Отже, одна ручка коштує 20 грн., тоді один блокнот коштує 20+9 = 29 грн.

Відповідь. Ручка коштує 20 грн., а блокнот – 29 грн.

IІІ. Домашнє завдання.    

Повторити §49, розв’язати вправи і задачі.

 

 

Використані джерела:

1.     Математика: Підручник 6 класу загальноосвітніх навчальних закладів./ О.С. Істер. – К.: Генеза, 2014.

2.     Математика за новою програмою. 6 клас.: за ред. Ірина Кирдей, Лариса Лемешко, Анатолій Бабенко. – К. : Бібліотека «Шкільного світу», 2014.

3.     Математика, 6 клас. Збірник самостійних робіт і тестів. / А.Г. Мерзляк, М.С.

Якір. – Харків, «Гімназія», 2021.