Розвиток пізнавальної активності учнів з обмеженими можливостями здоров'я під час уроків математики

Розвиток пізнавальної активності учнів

з обмеженими можливостями здоров'я

під час уроків математики

 

Актуальність теми

Історія інклюзивного навчання у світі розпочалася приблизно у 1970-х роках. Саме тоді в економічно розвинених країнах діти з особливими освітніми потребами (ООП) отримали можливість навчатися разом зі своїми ровесниками. Якщо говорити про офіційну дату запровадження такої форми навчання у світі, то нею можна вважати 9 грудня 1975 року. Саме в цей день Генеральна Асамблея ООН ухвалила Декларацію про права інвалідів. У цьому документі сказано: «Iнвaлiди, незважаючи на причину, характер i складність їхніх каліцтв або порушень, мають ті ж основні права, що і їхні співгромадяни того ж віку». Декларація затвердила, що інваліди мають отримувати необхідну підтримку, яка б дала змогу максимально виявити їхні можливості й здібності та прискорила б процес їхньої інтеграції в суспільство. Наступним документом, що сприяв упровадженню інклюзивної освіти й описав шлях реалізації Декларації ООН прав інвалідів, стали «Стандартні правила забезпечення рівних можливостей для інвалідів», що були затверджені 20 грудня 1993 року 48 сесією Генеральної Асамблеї ООН.

Якщо говорити про розвиток освіти в Європі, то на даний момент яскравим прикладом є освітні системи Австрії, Німеччини, Фінляндії, Швеції, Норвегії, Данії, Англії та Італії. У цих країнах інклюзивне навчання гармонійно інтегрувалося до системи загальної середньої освіти. В Україні інклюзивна освіта почала зароджуватися у 2001 – 2007 рр. Саме тоді МОН експериментально впровадило проект «Соціальна адаптація та інтеграція в суспільство дітей з особливостями психофізичного розвитку шляхом організації їх навчання у загальноосвітніх навчальних закладах». У рамках цього проекту розпочався пошук шляхів, що допомогли б здійснити інтеграцію дітей з ООП у процес навчання в загальноосвітніх навчальних закладах. З 2008 р. по 2012 р. реалізовувався укрaїнсько-кaнaдський проект «Інклюзивна освіта для дітей з особливими потребами в Україні». 1 жовтня 2010 року наказом МОН №912 було затверджено Концепцію розвитку інклюзивного навчання. 5 липня 2017 року Президент України розпочав велику освітню реформу й підписав ухвалений 23 травня 2017 року закон «Про внесення змін до Закону України «Про освіту» щодо особливостей доступу осіб з особливими освітніми потребами до освітніх послуг».

Розвиток пізнавальної активності – одне з найважливіших завдань сучасного вчителя. Особливо актуальне це питання для педагога, котрий працює з дітьми, які мають обмежені можливості здоров'я.

Учитель повинен знати, як донести важливу й корисну інформацію так, щоб вона привернула увагу, змусила задуматися, була доступна для розуміння дитини з особливими освітніми потребами.

Кожна дитина по-своєму унікальна, і потреби кожної дитини специфічні. Дитина з ООП на сучасному етапі розвитку суспільства розглядається як особистість, яка має ті ж права, що й інші члени спільноти, але через особливості індивідуального розвитку їй необхідно надавати особливі освітні послуги. Завдяки сучасній комплексній допомозі в дітей з особливими освітніми потребами спостерігаються позитивні зміни в особистісно-мотиваційній, пізнавальній, емоційно-вольовій сферах. Конвенція про права дитини та Декларація про права інвалідів, що були прийняті Генеральною Асамблеєю ООН, пріоритетними для дітей з особливими потребами назвали права на освіту, медичне обслуговування, професійну підготовку й трудову діяльність. Визнання нашою державою цих міжнародних документів підвищило увагу суспільства до проблем дітей з особливостями психофізичного розвитку, створення сприятливих умов для їхньої комплексної реабілітації.

Учитель у сучасній школі виступає не стільки «інформатором», скільки керівником, наставником, який спрямовує учнів до нових знань. Китайська мудрість говорить: «Скажи мені, і я забуду; покажи мені, і я запам'ятаю; дай мені зробити самому, і я зрозумію».

У відповідності до закону України «Про освіту» сьогодні кожна дитина з відхиленнями в розвитку має право на одержання адекватної її психофізичному розвитку освіти. Численні дослідження в галузі спеціальної педагогіки й психології підтвердили той факт, що правильно організована система навчання та виховання вказаної групи дітей дає свій позитивний ефект і призводить до їхнього значного просування в напрямку адаптації до життя в суспільстві.

У розвитку мотиваційної сфери існує безліч прийомів, які застосовуються відповідно до віку, індивідуальних особливостей учнів та навчального матеріалу. Різноманітні роботи активізують навчальну діяльність школярів, виховуючи в них самостійність мислення, уміння застосовувати знання в процесі навчання. Позитивний ефект дають різні дидактичні ігри, творчі завдання, практичні роботи, цікаві задачі... Новизна цієї теми полягає в тому, що відомі всім прийоми та методи сучасний вчитель може застосовувати в новій інтерпретації з використанням новітніх інформаційних технологій.

Особливо складним для дітей з ООП є засвоєння математики. Труднощі виникають через низький рівень пізнавальних процесів, таких як: увага, логіка, орієнтування у просторі та ін. Тому спостерігаються порушення розуміння структури  чисел, лівого та правого боку, складність у цифрових операціях при переході через десяток. Діти важко диференціюють геометричні фігури, відчувають труднощі при співвіднесенні їх з реальним предметом, в основі якого знаходяться.

Труднощі, з якими стикаються діти під час розв’язування задач:

– ознайомлення зі змістом задачі;

– перетворення простої задачі на складну;

 – аналіз задачі;

– пошук способу розв’язання (неправильний вибір арифметичної дії);

– розв’язання задачі;

 – помилки в обрахунках;

– відповідь та перевірка розв’язання задач.

 

Мета теми, можливість використання отриманого досвіду

в педагогічній діяльності

Мета: узагальнення досвіду роботи під час навчання математики учнів з обмеженими можливостями здоров'я в питаннях розвитку мотиваційної сфери та пізнавальної активності.

Даний досвід можна використовувати на уроках математики, алгебри, геометрії; під час індивідуальної роботи з учнями. Представлені компоненти системи роботи можливо адаптувати для школярів з різним рівнем успішності.

Методи, що використовуються, на мій погляд, дозволяють учителю вирішувати наступні завдання в навчальному процесі:

• мотивують учнів до самостійної роботи;

• розвивають творче мислення;

• формують навички практичної та дослідницької діяльності;

• систематизують знання з предмету.

Василь Сухомлинський сказав: «Без гри немає і не може бути повноцінного дитячого розвитку. Гра – це величезне світло, через яке в духовний світ дитини вливається життєдайний потік уявлень, понять про навколишній світ». Саме гейміфікація навчання допомагає педагогу задовольнити допитливість учня, залучити його до активного пізнання оточуючого світу, оволодіти способами пізнання, збагнути зв'язки між предметами та явищами.

 

Перелік компонентів системи роботи

Одним з основних і початкових завдань під час навчання математики є вироблення в учнів навичок хорошого рахунку. Проте одноманітність таких завдань, як приклади на обчислення, притупляє цікавість і до рахунку, і до уроків узагалі. Саме тому вчителю необхідно мати в запасі арсенал різних прийомів, що пов’язані з виробленням обчислювальних навичок учнів і водночас не дозволяють зловживати увагою дітей (особливо це стосується учнів з ООП, адже вони не спроможні тривалий час концентрувати свою увагу на одноманітних видах діяльності).

У молодших класах НУШ допускає розважальну складову в навчанні, тоді як у середній та старшій школі програма ускладнюється, тож не передбачає гейміфікації. Однак у дитини з особливими освітніми потребами може бути сформована недостатня мотивація до навчання, що заважатиме сприйняттю матеріалу, який не містить гри як елементу навчання. Як же діяти вчителю в цій ситуації?

Розглянемо добірку ідей, що допоможуть підтримувати зацікавленість дітей у вивченні математики в будь-якому класі.

1. У молодших класах учитель може використовувати для занять кубики, навчальну гру для вивчення таблиці множення, навчальні лінійки, соробан (рахунок подумки) тощо. 

Тут можна використовувати різноманітні ігри: «математичне доміно», кругові приклади, естафети, гру «Рибалка» (з кількох запропонованих прикладів учні 1 варіанту «виловлюють» приклади з відповіддю 5, а учні 2 варіанту – з відповіддю 6). «Математичне доміно», кругові приклади допомагають дітям здійснювати самоконтроль, а вчителю полегшують перевірку. Математична естафета підіймає в учнях дух змагання. Велику цікавість у дітей викликають завдання на виправлення навмисно зроблених помилок у розв’язку, на відновлення частково стертих записів, заповнення «кватирок» (приклад: зачинити «кватирки», щоб рівність була правильною). Ігровий компонент, дух змагання та творчості мають бути органічно введені в структуру всіх уроків, тоді заняття викликатимуть цікавість, бажання працювати й знати предмет. Використання сучасного мультимедійного устаткування дозволяє проводити цю роботу швидко, даючи вчителю можливість оперативно демонструвати правильні відповіді, контролювати отримані учнями результати.

Важливою складовою всіх уроків математики для дітей з обмеженими можливостями здоров'я є завдання на тренування математичної пам'яті та «зіркості». Більшість таких завдань базуються на знаходженні закономірностей (приклад: знайти закономірність і вставити значення).

2. У середніх класах учителям бажано включати в роботу «фініки»: під час виконання завдань додавати до кожного числового значення слово «фініки» (приклад: розв'язуючи нерівності, просіть порівняти, що більше – 632 фініки чи 753 фініків). Так дитина краще концентруватиметься на виконанні завдань. 

Якщо використані прийоми не допомогли дитині включитися в роботу, варто відвести її до ресурсної кімнати та зайняти чимось умовно корисним (наприклад, математичними іграми). У ресурсній кімнаті учневі може допомагати асистент учителя. Коли й це не покращило ситуацію, потрібно зателефонувати батькам дитини, бо така поведінка може свідчити про хворобу чи погане самопочуття.

3. Досить цікавий метод, який допоможе при вивченні предмету, – це «Нумікон». Методика «Нумікон» – універсальний спосіб навчити математики кожну дитину. Числа є доволі абстрактною категорією для молодших школярів, вивчити яку може бути не легко, тим більше, якщо йдеться про дітей з особливими освітніми потребами. Як  полегшити занурення школярів у світ математики й зробити інклюзивне навчання ефективнішим? Відповідь – «Нумікон»!

«Нумікон» – дієвий та інклюзивний підхід до викладання математики, розроблений Оксфордським університетом. Він розвиває математичні навички й задіює одразу декілька органів чуття (мультисенсорний метод). Принцип наочності втілюється в «Нуміконі» повної мірою: розмаїття фігурок, що символізують числа, сприяють якісному засвоєнню основ математики, розвитку дрібної моторики рук, уяви, логічного мислення та пам’яті. Украй актуальною така методика є для роботи з дітьми, які мають порушення розумового розвитку, дітьми з розладами аутичного спектру, синдромом Дауна, гіперактивністю тощо. Гра поєднує все: відчуття, візуальне сприйняття, думки, розмови, читання та письмо.

Як це працює? Основа «Нумікону» – різнокольорові фігурки з отворами, де останні демонструють числа від 1 до 10. Коли фігури стають у ряд, як на малюнку нижче, школярам легше побачити зв’язок між числами («на один більше», «на один менше») та зрозуміти відмінність між ними.

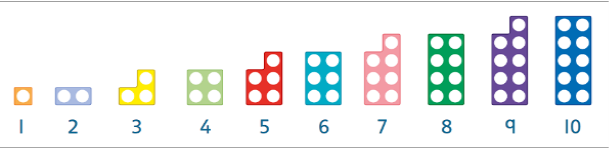
Математичні уроки перетворюються на гру-конструктор! Гра допомагає дітям не тільки навчитися арифметики, але й сформувати поняття про розміри та їх різницю, розвинути просторові уявлення, використовуючи завдання з конструювання та орієнтації на білій дошці тощо. Крім цього, за допомогою конструктора можна легко пояснити математичні дії, а саме: додавання, віднімання, множення, ділення.

4. Учням можна пропонувати як готові закономірності, так і можливість складати їх самостійно. Такий підхід дозволить активізувати творчий напрямок роботи, внести диференційований компонент до завдань.

Величезну роль у мотивації учнів до діяльності відіграють практичні завдання. Склеювання з паперу трикутної призми, паралелепіпеда, піраміди дозволяють школярам засвоїти поняття просторової фігури. Працюючи з дітьми, що мають порушення розвитку, я пропоную покроковий алгоритм виконання таких завдань, де кожен етап представлений для учнів на інтерактивній дошці. Такий підхід дозволяє більшості дітей упоратися з роботою, виправити помилки, орієнтуючись на покрокові моделі, показані на дошці.

5. Благодатним ґрунтом для формування практичних навичок є робота з транспортиром: вимірювання кутів, вирізування кутів певної градусної міри, розподіл кута на два рівні. Інтерактивна модель транспортира дозволяє вчителю продемонструвати алгоритм користування цим інструментом, уявити механізми побудови гострих, тупих, прямих кутів.

6. Велику цікавість у школярів 5-7 класів викликають уроки-казки. Вони особливо актуальні під час вирішення сюжетних завдань. Ця форма заняття не тільки робить навчальний процес захоплюючим, а й знімає емоційне напруження, страх учнів перед завданням.

Наприклад, при створенні уроку-казки в 5 класі з теми «Додавання і віднімання звичайних дробів з однаковими знаменниками» перед учителем будуть стояти такі завдання:

– навчальні: формувати поняття правильного і неправильного звичайного дробу; формувати уміння і навички учнів додавати та віднімати дроби з однаковими знаменниками;

– розвивальні: розвивати увагу, мислення, пам’ять, культуру математичного мовлення; розвивати вміння спілкуватись, аналізувати ситуацію, допомагати іншим, логічно мислити, застосовувати набуті знання в життєвих ситуаціях; продовжити розвивати загальнонавчальні навички (ведення зошита, організація роботи, робота з роздавальним матеріалом, застосування теоретичних знань для виконання завдань тощо); сприяти розвитку комунікативної, інформаційної, соціальної, полікультурної компетентностей;

– виховні: виховувати уважність, кмітливість, акуратність, працьовитість, самостійність, дисциплінованість, самокритичність.

Створення уроку-казки є досить цікавим. Розпочинаючи такий урок, ми наголошуємо, що він не звичайний, що ми потрапимо до казки. Потім пропонуємо пригадати відому казку Ганса Крістіана Андерсена «Снігова Королева» і підкреслюємо, що подорож разом з Гердою до Лапландії, щоб врятувати Кая із льодового королівства Снігової Королеви, відбудеться тільки після виконання деяких завдань. Нагадуємо, що казка ця не звичайна, а математична, тож на своєму шляху Герда зустріне математичні перешкоди. «Навряд дівчинка зможе сама впоратись із цими завданнями. Чи згодні ви допомогти їй?» – звертаємося до класу.

Отже, під час подорожі перед героїнею казки виникають різні завдання, які допомагають вирішувати учні.

Ставимо умову: Герда вирішила спитати в річки, чи не бачила вона Кая, і за відповідь готова була віддати свої нові червоні черевички. Але річка відмовилася від черевичків, а замість цього дала дівчинці завдання.

 

a	13 32		82   125	27   44		14   17
b	9   32	3   47		27   44	28   123
a + b			82   125			22   17
a – b		22   47			56   123

 

 

Ставимо умову: Кай із Гердою вийшли з пустельного крижаного палацу, та їх затримала Снігова Королева. Вона пообіцяла відпустити дітей тільки після  того, як вони знайдуть розв’язки прикладів.

 

 

Домашнє завдання теж краще подати у незвичній формі: «Діти, аби ви ще краще вдосконалили своє вміння виконувати додавання та віднімання дробів з однаковими знаменниками, попрацюйте вдома над завданнями від Снігової Королеви».

 Такі форми занять викликають цікавість до математики, а також сприяють створенню позитивної емоційної обстановки під час уроку, що особливо актуально для дітей з обмеженими можливостями здоров'я. Нестандартні форми уроку цінні тим, що водночас із формуванням зацікавленості предметом вони сприяють накопиченню знань, навичок та умінь.

Для розвитку пізнавальної активності учнів дуже корисні інтегровані уроки (математика-фізика, математика-біологія, математика-хімія). Цей підхід дозволяє вчителю як активізувати пізнавальну діяльність, так і продемонструвати міжпредметні зв'язки, що є невід'ємним завданням освітнього процесу.

7. Уроки-подорожі часто використовуються при вивченні теми «Завдання на рух». Змодельована ситуація дозволяє учням в ігровій формі засвоїти поняття відстані, швидкості й часу, що необхідно для складання математичної моделі під час розв’язування задач.

А) Річки України – це цінний водний запас, наші природні ресурси. А що ж таке річка? (Відповіді учнів.)

– Погляньте на схему, де зображено загальну довжину річок та їхню довжину в межах України. У якої річки найбільша довжина загальна, а найменша в межах України?

Які ж довжини найбільших річок України, ми дізнаємося, коли виконаємо завдання, що з’являтимуться на екрані.

Б) «Мозковий штурм». При виконанні завдань на екрані з’являються довжини річок:

Дніпро – 981 км

Дунай – 174 км

Дністер – 692 км

Сіверський Донець – 672 км

Десна – 591 км

Прут – 272 км

В) Розв’язування задачі:

У нашій країні протікає 131 річка завдовжки понад 100 км. Це в 31 раз менше, ніж річок довжиною понад 10 км. Скільки в Україні річок довжиною понад 10 км? (Скласти й записати лише вираз для розв’язання.)

131 х 31 = 4061

8. Дуже важливою в розвитку мотиваційної сфери є наявність під час уроку таких нестандартних завдань, як завдання-жарти та завдання-фокуси.

Приклади завдань-жартів:

1. Що легше: 1 кг цвяхів чи 1 кг вати?

2. Одне яйце варять 4 хвилини. Скільки хвилин варять 5 яєць?

3. Бігла трійка коней. Кожен кінь пробіг 5 км. Скільки км проїхав візник?

Завдання-жарти змушують учня не ставитися до розв’язку формально, часто не розуміючи його суті, а шукати каверзу, уважно вчитуватися в умову, моделювати ситуацію.

Приклади завдань-фокусів:

1. Задумайте число, помножте його на 4; результат помножте на 0,25. Назвіть відповідь, я назву задумане вами число. Поясніть, чому я це змогла зробити.

2. Задумайте тризначне число і припишіть до нього таке саме число. Отримане шестизначне число помножте на 2. Результат поділіть на 7, а потім той, що вийде, на 11 і, нарешті, на 13.

Запитайте учня, якою буде відповідь, і ви назвете задумане число, розділивши названу відповідь на 2.

Такі завдання пробуджують природну цікавість і змушують шукати пояснення фокусу. Корисні такі завдання для формування обчислювальних навичок. Учитель, розширюючи мотиваційну сферу школярів, під час вирішення дидактичних завдань дає можливість відчути красу математики, її багатопрофільність, різноманітність. Математика перестає бути предметом, що лякає своєю складністю, і починає ставати цікавою та життєво необхідною.

Сучасний педагог повинен використовувати при навчанні математики природну цікавість школярів і їхнє бажання розібратися в питанні. Для учнів старших класів важливе формулювання проблеми щодо конкретної теми, яку вони захочуть вирішити за допомогою математичних знань. 

Ці методи становлять органічну частину системи проблемного навчання, основою якої є створення проблемних ситуацій, формулювання проблем, підведення учнів до проблеми. Проблемна ситуація містить емоційний, пошуковий та вольовий компоненти. Її завдання – спрямувати діяльність учнів на максимальне оволодіння навчальним матеріалом, забезпечити мотиваційний бік діяльності, викликати цікавість до неї.

Активна розумова діяльність завжди пов'язані з вирішенням певного завдання. Думати людина починає, якщо в неї виникла потреба щось зрозуміти, щось здійснити. Мислення починається з проблеми чи питання, протиріччя. Проблемною ситуацією вважається залучення особистості до розумового процесу, який завжди спрямований на вирішення певного завдання. Використання проблемного методу навчання, на мій погляд, дуже важливе для дітей з ООП, оскільки сприяє розвитку розумової діяльності, а також дає дитині можливість відчути свою успішність.

Учитель повинен завжди йти в ногу з часом, уміти проводити паралелі між своїм предметом та подіями, що відбуваються у своєму місті чи в країні. Це дозволяє учневі зрозуміти зв'язок навчальних дисциплін з життєвими ситуаціями, формує його життєвий досвід і тим самим сприяє розширенню мотиваційної сфери.

Арифметичні задачі – це математична форма відображення реальних ситуацій через числові вирази. У процесі їх вирішення відбувається розвиток розумових здібностей учнів, їхнє знайомство з різними життєвими ситуаціями і пошук вирішення цих проблемних ситуацій. Наприклад, покупка товару в магазині, складання сімейного бюджету або здійснення банківських операцій.

Для більшої ефективності арифметичні задачі необхідно адаптувати під індивідуальні потреби кожного класу та кожного учня. Для цього при підготовці до уроку потрібно використовувати конструювання завдань. Т.Дюміна, М.Моісєєва, А.Смірнова визначають конструювання як практичну діяльність, спрямовану на отримання заздалегідь задуманого продукту з метою формування й розвитку певних навичок в учнів. Зважаючи на необхідність творчого підходу до навчання і врахування особливостей дітей, конструювання арифметичних задач посідає важливе місце в педагогічній діяльності вчителя математики. Однак, як показав аналіз методичної та навчальної літератури, питання конструювання задач у спеціальній школі висвітлене недостатньо глибоко й широко.

Розглянемо приклад конструювання арифметичної задачі для учнів 9 класу спеціальної школи-інтернату. У розділі підручника, де вивчаються десяткові дроби, наведені задачі про пошиття одягу, продаж тканини, ведення здорового способу життя, але не розглянуті реальні життєві ситуації, наприклад, ремонт у квартирі.

Зупинимося на конкретному прикладі з підручника: «Скільки сидінь для табуретів можна вирізати з листа фанери довжиною 4 м та шириною 1,6 м, якщо площа сидінь становить 40 см х 40 см?» Аналізуємо задачу. Текст має особливу структуру: умова й запитання знаходяться в одному реченні. Числові дані – десяткові дроби та цілі числа. Під час розв’язку необхідно виконати множення і ділення без залишку. Одиницями виміру в задачі є сантиметри й метри, відповідно, при розв’язанні закріплюються знання про співвідношення мір довжини. При конструюванні задачі ми зберігаємо структуру тексту, операції з числовими даними та одиниці виміру, але змінюємо ситуацію виготовлення стільця на уроці праці на ситуацію ремонту в квартирі, а конкретно – на укладку кахельної плитки у ванній кімнаті: «Скільки потрібно кахельних плиток для ванної кімнати, якщо її довжина 2,5 м, ширина 3,6 м, а площа плиток 30 см х 30 см?» У сконструйованій задачі ми зберегли математичну структуру початкового варіанту, але можливе продовження конструювання вихідної задачі. Можна змінити структуру тексту, наприклад, зробити так, щоб частково умова знаходилася в питанні або вся умова містилася в розповідному реченні, вимога знайти невідомий компонент – у питальному. Можна ускладнити завдання, змінивши розмір кімнати, запропонувавши ситуацію, коли плитку доведеться обрізати, або ж змінити розмір плитки у зв’язку зі зміною ситуації ремонту. Указану квадратну кахельну плитку можна замінити на стельову іншого розміру (50 см) для покриття стелі кімнати чи ввести в задачу кахельну плитку розміром 20 см х 30 см для «фартуха» на кухні. Таким чином, змінивши запитання і доповнивши умову новими даними (вартість плитки, кількість плиток в упаковці), можна збільшити кількість дій у задачі. При всіх цих змінах зберігається напрямок сюжету: ремонт у квартирі, а точніше – укладання плитки.

Доходимо висновку, що конструювання арифметичних задач має великий потенціал для соціалізації дітей з розумовою відсталістю. При конструюванні враховуються індивідуальні особливості школярів, рівень математичної підготовки конкретного учня (групи учнів, класу), рівень знань про навколишній світ, життя в соціумі, особливості соціальних умінь. Конструювання задач розширює межі можливостей педагогів. Правильно організований процес конструювання продукує новий матеріал для уроків та позаурочної діяльності; дає можливість вийти за межі підручників і застосувати елементи творчості в роботі вчителя, оскільки Інтернет не завжди може бути помічником у конкретній ситуації; дозволяє заощадити час для ефективного вирішення завдання соціалізації в конкретному учнівському колективі дітей з особливими освітніми потребами.

 

 

 

Використана література

1. Бондаренко М.В. Конструювання арифметичних задач на уроках математики, як засіб вирішення проблеми соціалізації дітей з особливими освітніми потребами.

2. Закон України «Про основи соціальної захищеності осіб з інвалідністю в Україні».

3. Колупаєва А.А. Діти з особливими потребами та організація їх навчання.

4. Коробейников І.А. Порушення розвитку та соціальна адаптація.

5. Приходько О.Г. Соціальний розвиток дітей з обмеженими можливостями здоров’я.

6. Унтіна М. Розвиток математичних компетентностей у дітей з ООП.