МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Державний заклад «ПІВДЕННОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ

ПЕДАГОГІЧНИЙ УНІВЕРСИТЕТ ІМЕНІ К. Д. УШИНСЬКОГО»

 

Навчально-науковий інститут природничо-математичних наук, інформатики та менеджменту

Кафедра вищої математики і статистики

 

 

 

 

Кваліфікаційна робота магістра

«Розв’язання трикутників»

 

 

 

 

 

Виконала: здобувачка  освітнього ступеня магістра  заочної форми навчання

ОПП «Середня освіта (Математика)» спеціальності  

014.04 Середня освіта (Математика)

Діордійчук Світлана Сергіївна Науковий керівник   к.т. н., доцент,

Урум Галина Дмитрівна 

 

 

 

 

 

 

Одеса – 2024 ВСТУП............................................................................................. 3

Розділ 1. ТЕОРИТИЧНІ ОСНОВИ ТЕОРЕМ СИНУСІВ ТА КОСИНУСІВ........... 6

1.1. Сучасні підручники геометрії для 9 класу та їх вплив на якість освіти........ 6

1.2. Порівняльний аналіз сучасних підручників з геометрії для 9 класу щодо теми "Теорема синусів та косинусів"........................................................................... 7

1.3. Теореми синусів та косинусів..................................................................... 14

1.3.1. Формулювання та доведення теореми синусів та її наслідків............... 15

   1.3.1.1. Теорема синусів та її доведення...................................................... 15

   1.3.1.2. Наслідки з теореми синусів та їх доведення.................................... 17

1.3.2. Теорема косинусів її наслідки, доведення та застосування................... 19

   1.3.2.1. Наслідки з теореми косинусів та їх доведення................................ 22

   1.3.3. Застосування теорем синусів і косинусів у науці та техніці............... 24

1.3.4.  Порівняння та взаємозв'язок між теоремами синусів та косинусів...... 26

1.4. Порівняння теореми синусів і теореми косинусів з теоремою Піфагора.... 28

1.4.1. Загальний огляд та формулювання теореми Піфагора.......................... 28

 

ЗМІСТ

1.4.2. Порівняння умов та областей застосування теореми Піфагора,

теореми синусів і теореми косинусів ................................................................ 27 Висновки до розділу 1 ............................................ Error! Bookmark not defined.

РОЗДІЛ 2. ГЕОМЕТРИЧНІ ЗАСТОСУВАННЯ ТЕОРЕМИ СИНУСІВ ТА

КОСИНУСІВ ............................................................................................................ 33

2.1. Розв'язання геометричних задач за допомогою теореми синусів ................ 33

2.2. Розв'язання геометричних задач за допомогою теореми  косинусів ........... 51

2.3. Задачі для самостійного розв’язування на теорему синусів ........................ 63

2.4. Задачі для самостійного розв’язування на теорему косинусів .................... 64

2.5. Методичні рекомендації щодо покращення подання теорем синусів і

косинусів школярам. ............................................................................................. 66

Висновки до розділу 2 .......................................................................................... 68

ВИСНОВКИ ............................................................................................................. 69

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ ................................................................. 71

ВСТУП

 

 

Теореми синусів і косинусів займають важливе місце в шкільному курсі геометрії. Вони є основними для розв'язання трикутників та знаходять широке застосування в багатьох галузях науки і техніки, таких як фізика, астрономія, інженерія. Тому успішне засвоєння учнями цих теорем має велике значення для подальшого вивчення математичних та природничих дисциплін.

Проте, вивчення цих теорем часто викликає труднощі в учнів. Це пов'язано як зі складністю самих теоретичних положень, так і з тим, що  викладання матеріалу в підручниках не завжди є доступним для опанування його учнями. На сьогоднішній день існує багато варіантів подання теорем синусів і косинусів, кожен з яких опирається на різні методи та підходи щодо їх доведення.

Тому я, як вчитель-практик,  зацікавилась методикою викладання даної

теми в різних підручниках, для того щоб для себе сформулювати найраціональший метод подання матеріалу в своїх 9-х класах. 

Мета дослідження:  проаналізувати порядок викладання теорем синусів і косинусів у сучасних підручниках з геометрії для 9-х класів, визначити їх ефективність, окреслити методичні рекомендації щодо покращення подання матеріалу школярам.

План досягнення поставленої  мною мети складається з наступних етапів:

1.                  Порівняння підходів щодо подання теорем синусів і косинусів у різних підручниках з геометрії 9-х класів.

2.                  Виявлення найбільш ефективних методик для покращення

засвоєння школярами даного матеріалу.

3.                  Оцінення значення наочності та практичних завдань, що містять підручники, на розуміння учнями теорем та вмінням їх застосовувати в подальшому.

4.                  Сформулювання методичних рекомендації для вчителів щодо вдосконалення викладання теорем синусів і косинусів з урахуванням в класах різними навчальними потребами.

Об'єкт дослідження: сучасні підручники з геометрії таких авторів: Єршова А.П, Мерзляка А.Г, Бевза Г.П., Бурди М.І., Апостолової Г.В. та Істера О.С.

Предметом дослідження є: послідовність викладання навчального матеріалу, науковий рівень поданння матеріалу, його доступність для учнів. Та характеристика практичних завдань, які подають автори підручників для вироблення в учнів вмінь та навичок щодо застосування даного навчального матеріалу.

В процесі мого дослідження я добирала свої вправи та завдання на застосування теорем, спираючись на свій практичний досвід з бажанням звернути увагу колег, вчителів математики, на потребу складати ще інші цікаві нестандартні задачі на застосування теореми.

Практичне значення дослідження: Матеріали дипломної роботи можуть бути використані для оптимізації викладання складних математичних понять. Зокрема:

1.                 Методистами та авторами підручників — для вдосконалення методик викладання тригонометрії.

2.                 Вчителі математики для підготовки та проведення уроків з більшою інтерактивних уроків, уроків вироблення практичних.

3.                 Студенти педагогічних спеціальностей як навчально-методичний матеріал для планування та проведення уроків під час практики або підготовки до власної викладацької діяльності.

4.                 Учні для самостійного опрацювання та закріплення знань, оскільки вправи та задачі мають різний рівень складності і спрямовані на розвиток навичок розв'язування задач з тригонометрії.

5.                 Педпрацівники, які готують учнів до складання зовнішнього незалежного оцінювання (ЗНО), з метою систематизування знання та натренування навичок розв’язання задач на застосування теореми косинусів та синусів.

6.                 Розроблений матеріал може використовуватися в позакласній роботі з математики, занять математичних гуртків, підготовки учнів до олімпіад та захисту робіт МАН.  

Апробація дослідження: результати дослідження представлені в матеріалах десятої міжнародної конференції з адаптивних технологій управління навчання та висвітлені на засіданні шкільного методичного об’єднання вчителів математики Овідіопольського ліцею імені Т.Шевченка.

       Структура роботи. Робота складається зі вступу, двох основних розділів, підсумкових висновків до кожного розділу, загальних висновків, списку використаних джерел і додатків.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ 1. ТЕОРИТИЧНІ ОСНОВИ ТЕОРЕМ СИНУСІВ ТА КОСИНУСІВ

 

1.1.    Сучасні підручники геометрії для 9 класу та їх вплив на якість освіти

У сучасному світі математична освіта є основою для розвитку науки та технічного прогресу. Однак, для багатьох учнів математика залишається складним і важким предметом. Однією з причин є недосконалість шкільних підручники, які ненадають можливості школярам самостійно опрацьовуввати навчальний матеріал та долати прогалини свої прогалини в знанях з математики. В даній роботі ми розглянемо основні вимоги до сучасних підручників геометрії для 9 класу та їх вплив на якість освіти, зокрема, на прикладі підручників Єршова, Бурди, Бевза, Апостолової, Мерзляка та Істера.

Основні вимоги до сучасних підручників математики:

1. Зрозумілість і доступність матеріалу: підручники повинні бути написані простою та зрозумілою мовою, з використанням графіків, діаграм та прикладів з реального життя для полегшення розуміння складних концепцій. 2.           Інтерактивність і залучення: важливо, щоб підручники сприяли активній участі учнів через інтерактивні вправи, цифрові технології та проєктні завдання, що покращує розуміння матеріалу.

3.                 Практична спрямованість_: підручники повинні демонструвати практичне застосування математичних знань у різних сферах, таких як наука, техніка, економіка, що допомагає учням побачити важливість математики у повсякденному житті.

4.                 Диференційований підхід: підручники повинні враховувати різні рівні підготовки учнів, пропонуючи завдання різного ступеня складності, що дозволяє кожному учневі працювати на своєму рівні.

5.                 Інтеграція з іншими предметами: математика повинна бути пов'язана з іншими науками, такими як фізика, хімія, біологія, інформатика, що дозволяє учням бачити цілісну картину знань.

6.                 Актуальність і оновлення: підручники повинні відображати новітні досягнення у математиці та педагогіці, оновлюватися відповідно до сучасних освітніх стандартів і наукових відкриттів.

7.                 Психологічна підтримка учнів: важливо, щоб підручники сприяли розвитку критичного мислення, впевненості у своїх силах і позитивного ставлення до навчання.

 

1.2. Порівняльний аналіз сучасних підручників з геометрії для 9 класу щодо теми "Теорема синусів та косинусів"

Дана тема розглядаються у різних підручниках для 9 класу закладів загальної середньої освіти, рекомендованих Міністерством освіти і науки України з геометрії, кожен з яких має свої особливості подання матеріалу, методичні підходи, а також переваги та недоліки. Мета цього порівняльного аналізу - виявити сильні та слабкі сторони підручників, що дозволить зробити вибір найбільш ефективного навчального ресурсу для учнів. Розглянемо підручники авторів Єршова А.П, Мерзляка А.Г, Бевза Г.П., Бурди М.І., Апостолової  Г.В. та Істера О.С., порівнємо їх за структурою подання матеріалу, методичними підходами, практичними задачами, а також визначимо перевагами та недоліками.

Аналіз підручників геометрії для 9 класу

Автор	Особливості підручника
Єршов А.П.	Підручник чітко та структуровано подає матеріал, використовує візуальні засоби, містить багато прикладів та
	завдань.
Бурда М.І.	Приділяє увагу практичному застосуванню теоретичних знань, містить інтерактивні вправи та проєктні задачі.
Бевз Г.П.	Пропонує завдання для самостійного виконання, інтеграції з іншими предметами та практичної спрямованості
Апостолова Г.В.	Використовує інтерактивні методи навчання, інтегрує геометрію з іншими науками, розвиває критичне мислення
Мерзляк А.Г.	Систематичне подання матеріалу, поступове нарощування знань, інтеграція геометрії з іншими науками
Істер О.С.	Орієнтований на диференційоване навчання, пропонує завдання різної складності для індивідуального підходу.

 

У підручнику з геометрії Мерзляка теореми синусів і косинусів розглядаються послідовно й доступно, з акцентом на наочність і поступовий розвиток навичок учнів. Автор починає тему з теоретичного обґрунтування теореми синусів, пояснюючи, як ця теорема встановлює зв’язок між сторонами трикутника і синусами його кутів. Хоча формула теореми синусів надається без доведення, автор підкреслює її значущість для розв’язання задач на обчислення невідомих сторін і кутів трикутника. Для полегшення розуміння наводяться чотири приклади, що ілюструють застосування цієї теореми в різних ситуаціях

[1].

Далі вводиться теорема косинусів, яка розглядається як узагальнення теореми Піфагора для будь-якого трикутника. Без доведення формули автор демонструє, як ця теорема дозволяє обчислювати довжину сторони трикутника за відомими двома іншими сторонами та кутом між ними. Графічні ілюстрації, які супроводжують пояснення, допомагають учням візуально сприймати й легше засвоювати матеріал.

Наступним етапом є практичне застосування теорем синусів і косинусів через серію задач різного рівня складності. Цей підхід дозволяє поступово підвищувати рівень складності, що сприяє розвитку навичок вирішення геометричних задач. Завдяки цьому учні мають змогу закріпити знання та впевнено використовувати отримані теоретичні знання на практиці.

Далі розглядається застосування теорем для обчислення площі трикутника, коли відомі деякі елементи, такі як сторони та кути. Автор наводить кілька задач із детальними поясненнями, що ілюструють різні випадки розв’язання, допомагаючи учням побачити застосування теорем в реальних задачах.

Після завершення теми Мерзляк узагальнює основний теоретичний матеріал і пропонує додаткові задачі, структуровані подібно до попередніх. Такий підхід дозволяє учням перевірити свої знання та впевнитися в правильному засвоєнні матеріалу щодо теорем синусів і косинусів.

Істер дотримується збалансованого підходу у викладанні, поєднуючи теоретичні основи, практичні завдання та наочність. Він подає матеріал з багатими поясненнями і прикладами, що забезпечує глибоке розуміння як теоретичних, так і практичних аспектів теми. Особливу увагу приділено повторенню та узагальненню знань, що допомагає учням закріпити матеріал[2].

У підручнику Істера О.С. теми «Теореми косинусів та синусів» містять геометричне доведення теореми косинусів для прямокутного трикутника та теорему синусів, що пов’язує хорду і діаметр з синусом вписаного кута. Ілюстрації допомагають краще зрозуміти цю теорію.

Істер також акцентує на практичному застосуванні теорем, наводячи приклади розв’язання задач різної складності, що дозволяє учням закріпити теоретичні знання і навчитися їх використовувати. Автор дотримується принципів наступності та диференційованості задач, що поступово підвищує навчальне навантаження.

Крім того, він розглядає застосування теорем синусів і косинусів для обчислення площі трикутника. У кінці теми Істер подає узагальнений теоретичний матеріал і серію задач, щоб учні могли перевірити свої знання і навички. Через різноманітні задачі він підкреслює важливість теорем синусів та косинусів у геометрії.

Бевз акцентує увагу на практичному застосуванні теорем, показуючи учням, як вони використовуються в реальному житті. Приклади з таких сфер, як геодезія або навігація, допомагають зрозуміти, як знання геометрії можуть бути корисними поза межами класу. Такий підхід робить навчання більш релевантним і цікавим, особливо для тих учнів, хто цінує практичність знань.

[3]

Розпочинаючи розділ 3 «Розв'язування трикутників», Бевз акцентує на доведенні теореми синусів як ключової для розв'язування трикутників. Він детально демонструє її застосування в різних геометричних задачах і надає графічні ілюстрації для забезпечення доступності матеріалу. Автор також включає приклади розв'язання задач з детальними поясненнями.

Бевз приділяє увагу завданням з практичним змістом, пов'язаним із застосуванням теорем синусів і косинусів. Це допомагає учням закріпити знання та навички через різноманітні задачі, які варіюються за рівнем складності. Такий підхід дозволяє поступово освоювати матеріал, розвиваючи логічне мислення. Підручник містить повні розв'язання значної кількості задач, що полегшує процес навчання.

Крім того, Бевз розглядає використання теорем синусів і косинусів для обчислення площі трикутника, підкреслюючи важливість і корисність задач практичного спрямування для школярів. Це допомагає учням не лише в навчанні, а й у майбутньому житті.

Основною особливістю підходу Бурди є велика кількість задач для самостійного розв’язання. Учні отримують широкий вибір завдань різного рівня складності, що стимулює активне навчання, розвиток критичного мислення та вміння застосовувати знання на практиці. Це особливо підходить для тих, хто прагне поглибити свої математичні здібності. [4]

Підручник Бурди починається з введення в теорему синусів. Автор чітко пояснює, що ця теорема встановлює співвідношення між сторонами трикутника та синусами протилежних кутів. Він детально розглядає формулу теореми, підкреслюючи її важливість для обчислення невідомих величин у трикутниках. Наведені приклади демонструють, як використовувати цю теорему в практичних ситуаціях, що допомагає учням краще засвоїти матеріал.

Далі Бурда переходить до теореми косинусів, наголошуючи, що вона є узагальненням теореми Піфагора і застосовується до будь-якого трикутника. Автор пояснює формулу теореми косинусів та демонструє, як її

використовувати для знаходження довжин сторін, якщо відомі дві сторони та кут між ними. Підручник містить ілюстрації та приклади, що сприяють засвоєнню матеріалу.

У розділі про практичне застосування теорем синусів і косинусів Бурда пропонує широкий спектр задач. Він наводить приклади різного рівня складності, що дозволяє учням поступово закріплювати свої знання. Задачі супроводжуються детальними розв’язаннями, що допомагає краще зрозуміти процес.

Бурда також розглядає використання теорем синусів і косинусів для обчислення площі трикутника, пояснюючи, як знайти площу, знаючи різні комбінації сторін і кутів. Автор наводить приклади задач з розв’язаннями, демонструючи практичну цінність теоретичних знань.

На завершення теми Бурда підсумовує основні положення теорем синусів і косинусів і пропонує підсумкові завдання для самостійної роботи. Це дозволяє учням перевірити свої знання та навички, набуті під час вивчення матеріалу. Автор підкреслює важливість цих теорем у геометрії та їх широке застосування в різних математичних задачах, що робить їх незамінними для подальшого вивчення предмету.

Теорема синусів є важливим інструментом у тригонометрії, описуючи відношення між сторонами і кутами трикутника. Вона стверджує, що відношення довжини сторони трикутника до синуса кута, протилежного цій стороні, є сталим для всіх трьох сторін. Ця теорема корисна в геометричних обчисленнях, зокрема, у геодезичних вимірюваннях та проектуванні.

Теорема косинусів розширює можливості теореми синусів і дозволяє працювати з трикутниками, знаючи дві сторони і кут між ними. Вона формулює зв'язок між довжинами сторін трикутника та косинусом одного з його кутів, підкреслюючи своє значення в тригонометрії. Застосування теореми косинусів дає змогу обчислювати невідомі параметри у складних геометричних задачах.

У підручнику Єршова акцент робиться на формальному обґрунтуванні математичних теорем, зокрема теореми синусів і косинусів. Автор пояснює ці теореми, дотримуючись суворої логічної послідовності та акцентуючи увагу на їх доведеннях. Такий підхід сприяє розвитку навичок логічного мислення і допомагає учням глибше зрозуміти теорію, що є особливо корисним для тих, хто цінує математичну строгость і логічні аргументи [5].

Крім теоретичних аспектів, Єршов розглядає й практичне застосування обох теорем. Автор підкреслює, що теореми не лише важливі для теоретичного навчання, але й активно використовуються в таких галузях, як фізика і техніка. Їхнє освоєння допомагає студентам ефективніше вирішувати практичні задачі, що виникають у реальному житті, роблячи ці теореми невід’ємною частиною курсу геометрії.

Знання теорем синусів і косинусів також сприяє розвитку аналітичних навичок. Студенти, які розуміють ці концепції, здатні застосовувати їх у складніших темах, таких як векторний аналіз і сферична тригонометрія. Застосування цих теорем дозволяє ефективніше вирішувати задачі, пов’язані з різними геометричними фігурами та їхніми властивостями.

Таким чином, теореми синусів і косинусів, описані у підручнику С. В. Єршова, є основоположними для вивчення геометрії. Вони не лише допомагають зрозуміти тригонометричні функції, але й мають широке практичне застосування. Освоєння цих теорем дозволяє студентам підготуватися до більш складних математичних задач і успішно використовувати їх у різних професійних сферах.

Підхід Апостолової базується на простих і зрозумілих поясненнях, що робить матеріал доступним для учнів з різними рівнями математичної підготовки. Це особливо корисно для класів із різнорівневими групами, де важливо забезпечити розуміння всіх учнів. Теорема косинусів, яка розглядається у підручнику, є продовженням і доповненням теореми синусів. Вона дозволяє обчислювати одну з сторін трикутника, знаючи дві інші та кут між ними. Це особливо корисно, коли теорема синусів не може бути застосована через недостатню інформацію, наприклад, у задачах, пов’язаних з обчисленням відстаней у складних ситуаціях[5].

Обидві теореми мають практичне застосування в різних сферах, таких як навігація, архітектура та інженерія. Знання цих теорем допомагає точно розраховувати параметри проектів, що сприяє підвищенню точності розрахунків і спрощенню процесу вимірювання. Це робить їх невід’ємною частиною навчального курсу з геометрії.

У підручнику Апостолової також розглядаються різноманітні приклади, які ілюструють застосування цих теорем у реальних задачах. Це допомагає студентам краще зрозуміти, як використовувати теореми на практиці і створює зв'язок між теорією та практикою, що є важливим для засвоєння матеріалу. Учні мають можливість вивчати ці теореми не лише в теоретичному аспекті, але й у контексті їх використання в житті.

Таким чином, теореми синусів і косинусів, представлені у підручнику Апостолової, є основою для подальшого вивчення тригонометрії та геометрії. Вони надають інструменти для розв’язання різноманітних задач, пов’язаних із трикутниками, і освоєння цих теорем є важливим кроком у підготовці студентів до роботи з більш складними математичними концепціями.

Порівняльний аналіз підручників з математики для 9-х класів на тему "Теорема синусів та косинусів" показує різні підходи авторів до подачі матеріалу. Підручник Мерзляка виділяється своєю структурованістю та детальними поясненнями. Автор надає багато прикладів та задач, що сприяє кращому розумінню теми. Недоліком може бути дещо складний виклад теорії для учнів із середнім рівнем знань [1].

Істер також використовує багато прикладів, але його підручник більш орієнтований на теоретичне розуміння. Учні можуть відчути недоліки у практичному застосуванні знань, через відсутність достатньої кількості задач на закріплення. Перевагою є чіткість та логічність викладу, що допомагає краще засвоїти теоретичні аспекти [2].

Підручник Бевза пропонує збалансований підхід між теорією та практикою. Він містить як теоретичні виклади, так і велику кількість задач різного рівня складності. Це робить його універсальним та придатним для учнів з різним рівнем підготовки. Проте, подекуди зустрічаються складні для розуміння терміни без достатнього пояснення [3].

Бурда надає матеріал з акцентом на інтуїтивне розуміння теорем. Підручник включає цікаві історичні факти та приклади з реального життя, що робить його цікавим для учнів. Однак, іноді не вистачає формальних доказів і чітких пояснень, що може бути недоліком для глибокого вивчення теми [4].

Єршов та Апостолова в своєму підручнику також пропонують збалансований підхід. Вони включають багато ілюстрацій та схем, що допомагають візуально зрозуміти матеріал. Проте, підручник може бути занадто детальним для деяких учнів, що ускладнює процес навчання [5] [6].

Загалом, кожен з підручників має свої переваги та недоліки. Найбільш універсальним можна вважати підручник Бевза, оскільки він добре збалансований між теорією та практикою. Для учнів, які віддають перевагу детальним поясненням та структурованому матеріалу, краще підійде підручник Мерзляка. Якщо важливо інтуїтивне розуміння та цікавість матеріалу, варто обрати підручник Бурди.

 

1.3.Теореми синусів та косинусів

 

  Теореми синусів і косинусів є ключовими інструментами тригонометрії, що використовуються для розв'язання задач, пов'язаних з властивостями трикутників. Вони мають велике значення для вирішення практичних проблем у різноманітних наукових та технічних сферах.

1.3.1. Формулювання та доведення теореми синусів та її наслідків

1.3.1.1. Теорема синусів та її доведення

Теорема синусів є важливою частиною шкільної програми з математики у багатьох країнах. Вона допомагає учням зрозуміти основні принципи тригонометрії, розвивати логічне мислення та навички розв'язування задач. Теорема встановлює взаємозв'язок між сторонами трикутника та його кутами, що сприяє глибшому розумінню геометрії та розв’язанню складних задач.

                                                            Дано: ⊿ABC:

А

           𝛼 𝛽, 𝛾 − кути трикутника  

Довести,.

С

Застосування теореми синусів у розв’язуванні задач розширює можливості в аналізі та розумінні геометричних конструкцій. Вона дозволяє визначати відношення між сторонами трикутника та синусами відповідних кутів, що є корисним для знаходження невідомих сторін та кутів, а також для обчислення площі трикутника. Доведення теореми ґрунтується на поняттях площі та тригонометричних функцій.  

 Теорема  синусів

   Сторони трикутника пропорційні синусам протилежних кутів:

, де

a, b, c - сторони трикутника, протилежні кутам 𝛼 𝛽, 𝛾 відповідно

І спосіб (використовуючи  площу трикутника):

Доведення :

Розглянемо   ⊿ABC  зі сторонами a, b, c і відповідними протилежними кутами  𝛼, 𝛽, 𝛾. За теоремою про площу трикутника маємо:

S.

Прирівняємо   формули (1) та (2), отримаємо :

 

1

Поділимо ліву і праву частину на вираз   a, отримаємо : 2

b ∙  sin𝛾  = c ∙  sin𝛽, звідси       

          Зіставивши дві формули  (2) та (3) площі, отримаємо :

                                                                                                a                b

, звідси  

 

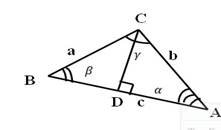Спосіб 2  (розкладання трикутника на прямокутні трикутники) Дано: ⊿ABC:

           a, b, c- сторони трикутника;

           𝛼 𝛽, 𝛾 − кути трикутника  

                                                                                                    Довести, .

а)  для гострокутного або тупокутного трикутника:

 Нехай у  довільному⊿ABC:  

ВС=a, АС=b, АВ=c,  ∠𝐴 = 𝛼, ∠В = 𝛽, ∠С = 𝛾.

Проведемо  з  вершини C до сторони АВ висоту CD, яка поділить трикутник  АВС на два прямокутні трикутники. 

 Розглянемо  прямокутний  ⊿ACD(∠𝐷 = 90°):

Якщо ∠𝐴– гострий, маємо CD= b ∙  sin𝛼;

Якщо ∠𝐴– тупийй,   маємо CD= b ∙  sin(180° − 𝛼) = b ∙  sin𝛼 Аналогічно в ⊿ВCD(∠𝐷 = 90°) , маємо CD= а ∙  sin𝛽.

CD-спільна сторона ⊿ACD і ⊿ВCD, а тому прирівняємо отримані вирази:

.

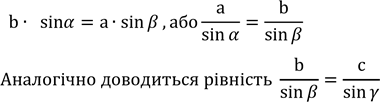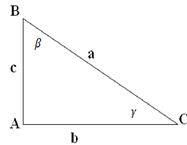б) для прямокутного трикутника:

В  за означенням синуса кута, маємо:

.

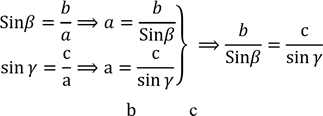Отже,

1.3.1.2. Наслідки з теореми синусів та їх доведення

 

Наслідок 1. Відношення  сторони до синуса протилежного кута дорівнює

діаметру кола, описаного навколо цього :

 

a, b, c - сторони трикутника, протилежні кутам  , R – радіус кола, описаного навколо трикутника.

                                                 Дано:ABC:

 

           a, b, c- сторони трикутника;

        

Довести, .

                          Доведення:

Опишемо навколо заданного трикутника АВС коло радіуса  R із вершини С проведемо діаметр СD=2R., як кут що спирається на діаметр.

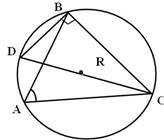
1)    Якщо – гострий, то він спирається як і кут  CDB на  дугу CB, тоді вони рівні (наслідок  з теореми про вписані кути). 

         B трикутнику СBD (:  

 

      .

2) 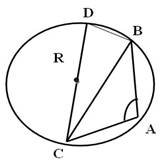   Якщо – тупий, то +°(за властивістю вписанного в коло  чотирикутника ABCD)

° .

B трикутнику СBD (:  

а

                                                                                                   .

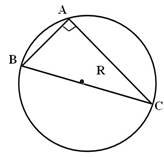3) Якщо – прямий, маємо:

 .          

Таким чином  для довільного трикутника ABC 

   

Отже,  

Наслідок 2.  У трикутнику проти більшої сторони лежить більший кут, проти більшого кута лежить більша сторона.

 

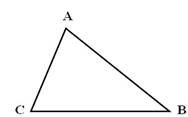
а) Дано: ABC- гострокутний ,

            0° < < 90°, 0° < < 90°, >. 

                                                                                                                Довести, що ВС > АС.

Доведення:

  

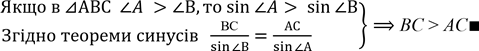
                                                                                А      б)  Дано: ABC- тупокутний ,

                90° <  < 180°                                          

                                                                                 ^С                      Довести, що АВ> АС.

Доведення:

Оскільки 90° <  < 180°, то 0° < 180° - < 90°, 180° -  =   180° -    sin = sin(180°- ) > sin . 

Враховуючи теорему синусів:

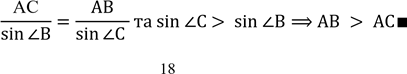
                                                                                          в)    Дано: ⊿ABC, АВ > АС. 

В 

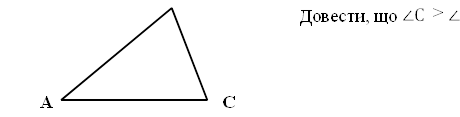
                                                                                             Доведення

Припустимо, що ∠С < ∠В, тоді згідно(а) ⟹АВ< АС , що суперечить умові  АВ > АС.   Якщо∠С = ∠В,то АВ = АС, що теж суперечить умові АВ > АС. 

Отже, припущення неправильне, тоді ∠С  > ∠В∎

Наслідок 3. (властивість бісектриси) Бісектриса кута  ділить протилежну сторону на відрізки, пропорційні до прилеглих сторін. 

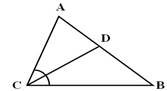 Дано: ⊿ABC, CD- бісектриса.

 

 

Доведення:

Нехай у  довільному ⊿ABC  проведемо  з  вершини C бісектрису CD  , яка поділить ⊿АВС на два ⊿ACD та ⊿BCD.

Запишемо  теорему синусів для :

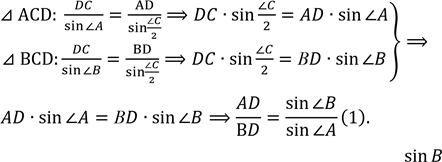                                    СА   СВ  СА

⊿ AВС: =          ⟹ С𝐴 ∙ sin 𝐴 = СВ ∙ sin В ⟹   =    (2)sin В     sin А  sin 𝐴  СВ

 

1.3.2. Теорема косинусів її наслідки, доведення та застосування

Теорема  косинусів

 Квадрат будь-якої сторони трикутника  дорівнює сумі квадратів двох

інших сторін без подвоєного добутку цих сторін на косинус кута між ними:

,

  

 

Дано:ABC,  АВ = c, АС = b, ВС=a і А= 

 

 

Доведення:

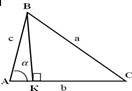
І спосіб (геометричний підхід із застосуванням висоти трикутника)   ВABC проведемо висоту ВК данного трикутника і знайдемо квадрат сторони BC  за теоремою Піфагора з  BКC.

Розглянемо три випадки оскільки кут  може бути гострим ,тупим або прямим.

1)    -гострий (°),то ВК=с,

 АК=сCК=АС-АК=b- с                                       

ВС ВК СК

 .

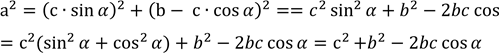
2)    -тупий (),то

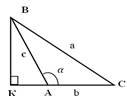 ВК=с, 

АК=с,

КС =АС + АК= b + (- с )= b - сЯк і в 1), маємо:

.

3) 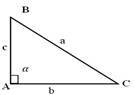   Якщо -прямий (), то ABC – прямокутний і

.За теоремою Піфагора

 

Отже, яким би не був кут  ABC завжди  

  

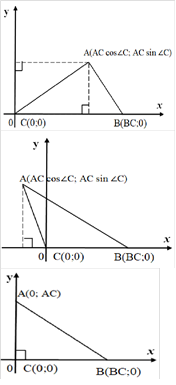
ІІ спосіб (координатний) [6, стор.51]

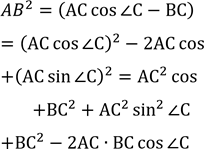
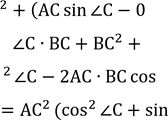
Введемо систему координат із початком  у точці С  Тоді точки А і В мають координати:

   А (АС cosC; АС sin C) і В(ВС;0).

Запишемо квадрат відстані між точками А і В у координатах:

Врахуємо, що  =1(основна тригонометрична тотожність)

Маємо:   

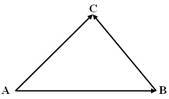ІІІ спосіб (векторний)   З рисунку маємо векторну

рівність:піднесемо її скалярно до квадрату, маємо:     

В правій частині застосуємо формулу скороченого    множення квадрат різниці ,отримаємо:      

Використавши  властивості скалярного добутку, отримаємо:

 

Зауваження: Теорема Піфагора є частковим випадком теореми косинусів для прямокутного трикутника, тому її інколи називають узагальненою теоремою Піфагора.

Дійсно, якщо в ABC – прямокутний ( – прямий), то підставивши в рівність             ,       , отримаємо:

- теорема Піфагора.  

  1.3.2.1. Наслідки з теореми косинусів та їх доведення

Наслідок 1. Квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін «±» подвоєний добуток однієї з них на проекцію другої. Знак «+» беремо тоді, коли протилежний кут тупий, а знак «–», коли гострий. [4, стор.29]

Доведення :

 

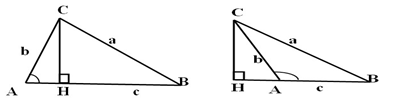
               Рис.1                                         Рис. 2

Для ⊿ABC теорема косинусів стверджує: 𝑎² = 𝑏² + 𝑐² − 2𝑏 ∙ 𝑐 ∙ cos ∠𝐴

 

З ⊿AНC(∠Н = 90°): АН =|𝑏 ∙ cos 𝐴|, де АН- проекція АС на АВ(рис.1) або її продовження(рис.2) .Знак 𝑏 cos 𝐴 залежить від кута А, якщо ∠𝐴 − гострий, то беремо «+», якщо тупий ,то «-»

Наслідок 2.  У  ⊿ABC зі сторонами a, b, с і ∠С між сторонами а і b

 

Доведення:

У  ⊿ABC за  теоремою косинусів 𝑐² = 𝑎² + 𝑏² − 2𝑎 ∙ 𝑏 ∙ cos С, маємо:

2𝑏 ∙ 𝑎 ∙ cos С = 𝑎² + 𝑏² − 𝑐².  

Поділимо ліву і праву частину на 2ab, отримаємо:    

Наслідок 3.  Якщо в  ⊿ABC зі сторонами a, b, с справджуються нерівність

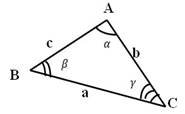а² + 𝑏² > с²,то ∠С − гострий; а² + 𝑏² < с²,то ∠С − тупий; а² + 𝑏² = с²,то ∠С − прямий.

                                                                                                                 Доведення:

Для ⊿ABC теорема косинусів стверджує:  с² = 𝑏² + 𝑎² − 2𝑏 ∙ 𝑎 ∙ cos С.

1)Запишемо нерівність:а² + 𝑏² > с²

Підставимо вираз для с², з теореми косинусів, отримаємо :

 𝑎² + 𝑏² > 𝑏² + 𝑎² − 2𝑏 ∙ 𝑎 ∙ cos С   - (𝑎² + 𝑏²);

  0 > −2𝑏 ∙ 𝑎 ∙ cos С  ∶ (−2ав); (оскільки a і b додатні):

cos С > 0 ⟹ ∠С − гострий,оскільки косинус додатній для гострих кутів(кутіввід 0°до90°).

2)  Якщо  а² + 𝑏² < с²,то  𝑎² + 𝑏² > 𝑏² + 𝑎² − 2𝑏 ∙ 𝑎 ∙ cos С   − (𝑎² + 𝑏²); Поділимо ліву і праву частину на вираз -2ab (оскільки a і b додатні):

                                      cos С < 0 ⟹ ∠С − тупий,оскільки    косинус    від’ємний    для    тупих                                                кутів

(кутіввід 90°до 180°).

3)  Якщо а² + 𝑏² = с²,то  𝑎² + 𝑏² = 𝑏² + 𝑎² − 2𝑏 ∙ 𝑎 ∙ cos С

Віднімемо 𝑎² + 𝑏²  від обох частин нерівності:  0 = −2𝑏 ∙ 𝑎 ∙ cos С

Поділимо ліву і праву частину на вираз -2ab (оскільки a і b додатні):

cos С = 0 ⟹ ∠С − прямий,  оскільки косинус дорівнює нулю для прямого кута(90°)∎

Наслідок 4. У паралелограмі сума квадратів діагоналей паралелограма  дорівнює сумі квадратів усіх його сторін : 𝐴𝐶² + 𝐵𝐷² = 2(𝐴𝐵² + ВС²). [6, стор.51]

 

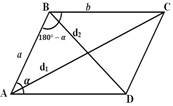
Дано: ABCD-паралелограм,

Довести, що: 𝐴𝐶² + 𝐵𝐷² = 2(𝐴𝐵² + ВС²).

     

                                 Доведення

Розглянемо  паралелограм ABCD ізгострим ∠A=𝛼,тоді  типий ∠B=180°-α . 

За теоремою косинусів із трикутника ABD:

𝐵𝐷² = 𝐴𝐵² + 𝐴𝐷² − 2𝐴𝐵 ∙ 𝐴𝐷 ∙ cos ∠𝐴 = 𝐴𝐵² + 𝐴𝐷² − 2𝐴𝐵 ∙ 𝐴𝐷 ∙ cos 𝛼

За теоремою косинусів у трикутнику ABС:

АС² = 𝐴𝐵² + ВС² − 2𝐴𝐵 ∙ ВС ∙ cos ∠В = 𝐴𝐵² + ВС² − 2𝐴𝐵 ∙ ВС ∙ cos(180° − 𝛼) = 𝐴𝐵² + ВС² − 2𝐴𝐵 ∙ ВС ∙ (−cosα) = 𝐴𝐵² + ВС² + 2𝐴𝐵 ∙ ВС ∙ cos 𝛼.

Почленно додамо ліві й праві частини рівності (1) і (2), отримаємо:

АС² + 𝐵𝐷² = 𝐴𝐵² + 𝐴𝐷² − 2𝐴𝐵 ∙ 𝐴𝐷 ∙ cos 𝛼 + 𝐴𝐵² + ВС² + 2𝐴𝐵 ∙ ВС ∙ cos 𝛼 =

= 2𝐴𝐵² + 2ВС², щоітребабулодовести∎

  Тобто в будь якому паралелограмі справджується рівність:

,

де 𝑑₁, 𝑑₁ − діагоналі  паралелограма;  а, b- сусідні сторони паралелограма.

Наслідок 5. Квадрат медіани, проведеної до сторони трикутника дорівнює півсумі квадратів двох інших сторін цього трикутника мінус чверть квадрата сторони, до якої проведено медіану. [6, стор.51]

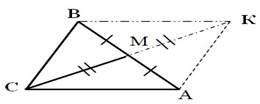
Дано: ⊿ABC, АВ=c, АС=b, ВС=a;

               CM = 𝑚_𝑐 − медіана.

. 

Продовжимо медіану 𝑚_𝑐 на відрізок MK=𝑚_𝑐. Утворений чотирикутник АСВК- паралелограм(бо СM=MK, AM=MB). Тоді за властивістю діагоналей

і сторін паралелограма, маємо    𝑑₁² + 𝑑₂² = 2𝑎² + 2𝑏²

.

Тобто для медіани 𝑚_𝑐 трикутника АВС виконується рівність:

 

         

1.3.3. Застосування теорем синусів і косинусів у науці та техніці

Теореми синусів і косинусів є основними інструментами тригонометрії, які мають численні та різноманітні застосування в науці та техніці. Їх використання дозволяє вирішувати складні геометричні задачі, пов'язані з вимірюванням відстаней, кутів, а також з аналізом сил та траєкторій руху. Ось декілька важливих сфер, де ці теореми знайшли своє застосування:

ü    Математика: Теореми синусів і косинусів використовуються для розв’язування геометричних задач, таких як обчислення сторін і кутів у трикутниках, визначення типу трикутника (гострокутний, тупокутний, прямокутний) та розрахунків діаметрів і радіусів описаних кіл. 

ü    Фізика: У фізичних науках ці теореми використовуються для аналізу руху тіл, визначення напрямків і величин сил, що діють на об’єкти під різними кутами. Вони дозволяють розраховувати компоненти сили тяжіння, моменти сил і навіть шляхи руху об'єктів.

ü    Астрономія: Теореми синусів і косинусів використовуються для розрахунків відстаней між небесними тілами та визначення кутових розмірів об'єктів на небосхилі. Це важливі інструменти для точних астрономічних вимірів і розрахунків.

ü    Комп'ютерна графіка: У тривимірному моделюванні та рендерингу ці теореми застосовуються для обчислення перспективи, кутів і відстаней між об'єктами в сценах, що дозволяє створювати реалістичні зображення і анімації. ü Навігація: Теореми використовуються в мореплавстві та авіації для розрахунку відстаней між об'єктами, визначення курсів руху і навігації суден та літаків, що є критично важливим для безпеки транспорту.

ü    Геодезія та картографія: У геодезичних розрахунках, що включають визначення відстаней між географічними точками, теореми синусів і косинусів є основою для виконання точних вимірювань і розробки карт, що допомагають у плануванні трас і меж земельних ділянок.

ü    Будівництво та архітектура: У цих сферах ці теореми допомагають розраховувати відстані та кути між елементами конструкцій, що забезпечує правильність геометрії будівель і конструкцій(покрівлі, сходи чи арки).

ü    Механіка         і         машинобудування:      В       машинобудуванні          та      аналізі

механічних систем ці теореми використовуються для визначення навантажень, деформацій і сил, що виникають під певними кутами, що критично важливо для забезпечення стабільності і надійності конструкцій.

ü    Космонавтика: Теореми синусів і косинусів використовуються для розрахунків траєкторій польоту космічних апаратів, що допомагає точно визначати їхнє положення та орбіти. Це важливо для виконання місій і безпеки космічних подорожей.

ü    Робототехніка і автоматизація: Теореми застосовуються для розрахунку кутів руху роботів, орієнтації рухомих елементів і точного виконання автоматизованих процесів. Вони використовуються в виробничих лініях і системах автоматизованого вимірювання.

Застосування теорем синусів і косинусів охоплює багато різних галузей, від класичних математичних задач до складних інженерних розрахунків, що підвищує точність і ефективність наукових і практичних досліджень. Вони є невід'ємною частиною сучасних технологій і науки, допомагаючи вирішувати найрізноманітніші задачі в математичному моделюванні, фізиці, інженерії та інших областях.

1.3.4.  Порівняння та взаємозв'язок між теоремами синусів та косинусів

Теореми синусів та косинусів взаємодоповнюють одна одну у вирішенні тригонометричних задач. Теорема синусів часто використовується у випадках, коли відомі кути і одна сторона, тоді як теорема косинусів застосовується, коли відомі всі три сторони або дві сторони і кут між ними. Разом вони забезпечують повний набір інструментів для точного розв'язання трикутників у різних галузях науки та техніки, визначення типу трикутника (гострокутний, тупокутний, прямокутний), розрахунку медіан та взаємозв'язку між діагоналями паралелограма.

Порівняння та взаємозв'язок між теоремами синусів та косинусів у табличній формі:

№	Критерій	Теорема синусів	Теорема косинусів
1.	Формулювання	a            b           с       =   =                   = 2𝑅	𝑎2 = 𝑐2 + 𝑏2 − 2𝑐 ∙ 𝑏 ∙ cos 𝛼 𝑏2 = 𝑐2 + 𝑎2 − 2𝑐 ∙ 𝑎 ∙ cos𝛽 𝑐2 = 𝑏2 + 𝑎2 − 2𝑏 ∙ 𝑎 ∙ cos𝛾

 

2.	Застосування у трикутниках	Використовується     для визначення     співвідношень між сторонами та кутами	Використовується для визначення довжини сторони або кута
3.	Спільне  використання	Використовується     разом з теоремою       косинусів       для розв'язання     комплексних тригонометричних задач	Доповнює               теорему синусів при розрахунках, коли відомі всі три сторони або дві сторони і кут між ними
4.	Розв'язання трикутників	Допомагає знайти невідомі сторони або кути за допомогою відомих співвідношень	Використовується для розрахунку довжини сторони при відомих інших сторонах і куті між ними
5.	Сфера  застосування	Навігація,               картографія, астрономія, будівництво	Навігація,       картографія, астрономія, будівництво, механіка, інженерія
6.	Визначення виду трикутника	Допомагає      визначити             тип трикутника             (гострокутний, тупокутний, прямокутний) на основі співвідношень між сторонами та кутами	Використовується              для перевірки, чи є трикутник прямокутним  (𝑐2 = 𝑎2+𝑏2) Гострокутним (𝑐2 < 𝑎2+𝑏2)    Тупокутним( 𝑐2 > 𝑎2+𝑏2)
7.	Медіани	Медіани не можуть бути безпосередньо розраховані, але теорема синусів може допомогти визначити кути, необхідні для подальших розрахунків	Використовується     для розрахунку     медіан трикутника    через формулу       де, 𝑚𝑎, 𝑚𝑏та 𝑚𝑐- медіани трикутника проведені до
			відповідних               сторін трикутника - a, b, c
8.	Взаємозв'язок між діагоналями паралелограма	Теорема синусів може бути використана для визначення кутів між діагоналями, якщо відомі сторони та один з кутів паралелограма	Використовується для розрахунку довжин діагоналей через формулу:  𝑑12 + 𝑑22 = 2𝑎2 + 2𝑏2 ,  де 𝑑1, 𝑑1 − діагоналі будь якого паралелограма з сусідніми сторонами a і b
9.	Взаємозв'язок	Доповнює теорему косинусів у задачах з відомими кутами	Доповнює     теорему синусів            у          задачах           з відомими сторонами

1.4. Порівняння теореми синусів і теореми косинусів з теоремою Піфагора

1.4.1.Загальний огляд та формулювання теореми Піфагора

 

Розглянемо сучасне доведення теорем Піфагора з використанням метричних співвідношень в прямокутному трикутнику  Теорема Піфагора

У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів, тобто АВ² =АС² + ВС² ,де АС і  ВС- катети трикутника, а АВ-

гіпотенуза.А  

 

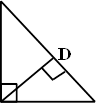
 Дано:⊿ABC, ∠ С=90°

 Довести, що: АВ² =АС² + ВС².

                                                           С                         В

                                       Доведення  

В прямокутному трикутнику  АВС ( ∠ С=90°) проведемо висоту СD з вершини С. Утворились  два прямокутні трикутники АDС і DВС, які подібні

⊿АВС і подібні між собою. З того, що ⊿АDС ~ ⊿ АВС,

АС²=АВ∙АD, де АС катет прямокутного трикутника є середнім пропорційним між гіпотенузою АВ і проекцією АD цього катета на гіпотенузу. 

З того, що ⊿ DВС~ ⊿ АВС, де ВС катет

прямокутного ⊿ АВС є середнім пропорційним між гіпотенузою АВ і проекцією ВD катета ВС на гіпотенузу АВ. 

Додамо рівності, врахувавши, що АD  +DВ = АВ. 

Маємо:  АС² + ВС² = АВ ∙ (АD + DВ) = АВ ∙ АВ = АВ²  

Отже,  АВ² = АС² + ВС²∎  

1.4.2.Порівняння умов та областей застосування теореми Піфагора, теореми синусів і теореми косинусів

Для точного вибору методу розв'язання геометричних задач і розуміння відмінностей між ними, порівняння умов застосування теореми Піфагора, теореми синусів і теореми косинусів є важливим. Ця інформація детально представлена в таблиці, що допомагає також у їх практичному застосуванні в різних галузях математики і науки:

№пп	Критерій	Теорема Піфагора	Теорема синусів	Теорема косинусів
1.	Тип  ⊿	Прямокутний ⊿	Будь-який ⊿	Будь-який трикутник
2.	Необхідні умови	Відомі довжини двох катетів або одна сторона і гіпотенуза	Дві сторони і протилежний кут або  дві сторони і кут між ними	Три сторони для знаходження кута або дві сторони і кут між ними для знаходження третьої сторони
3.	Основні        застосуван ня	Визначення сторін, діагоналі прямокутників	Розрахунок сторін, кутів	Визначення сторін, кутів, складні геометричні розрахунки
4.	Переваги	-                 Простота використання в прямокутних трикутниках; -                 широке застосування в різних	- Універсальність для будь-якого трикутника;  - гнучкість у знаходженні сторін і кутів.	-                  Універсальність до будь-якого трикутника; - корисна для пошуку сторін і кутів; -                  розширені можливості для розв'язання
		сферах ;                          - є основою для багатьох інших теорем		складних задач.
5.	Обмеження	Застосовується тільки до прямокутних трикутників	Потребує знання двох сторін і відповідного кута або трьох кутів	Може бути складною для використання без калькулятора або програмного забезпечення
6.	Формулюв ання теореми	𝑐2 = 𝑎2 + 𝑏2, де a і b- катети трикутника, а с- гіпотенуза	a, b, c- сторони трикутника, протилежні кутам 𝛼,𝛽, 𝛾	𝑎2 = 𝑐2 + 𝑏2 − 2𝑐 ∙ 𝑏 ∙ cos𝛼 𝑏2 = 𝑐2 + 𝑎2 − 2𝑐 ∙ 𝑎 ∙ cos 𝛽 𝑐2 = 𝑏2 + 𝑎2 − 2𝑏 ∙ 𝑎 ∙ cos 𝛾 a, b, c- сторони трикутника, протилежні кутам 𝛼 𝛽, 𝛾
7.	Геометрич ний сенс	Довжина гіпоте-нузи визначається через катети	Співвідношення сторін та синусів кутів	Зв'язок між сторонами і кутами
8.	Зв'язок з іншими теоремами	Є окремим випадком теореми косинусів	Включає теорему Піфагора як окремий випадок	Узагальнює теорему Піфагора
9.	Складність   обчислень	Дуже проста	Помірна склад-ність, потребує тригонометричних обчислень	Складніша, потребує знання тригонометрії
10.	Умови               застосуван ня	Застосовується      виключно для прямокутних трикутників	Застосовується для будь-якого трикутника, коли відомі достатні дані про сторони і кути	Застосовується для будь-якого трикутника, коли відомі всі сторони або достатньо сторін і кутів

Висновки до розділу 1

У цьому розділі було проведено глибокий аналіз сучасних підручників з геометрії для 9 класу, зосередившись на трьох основних тригонометричних теоремах: теоремі Піфагора, теоремах синусів і косинусів. Різноманітність підходів, представлених у підручниках авторів Мерзляка, Істера, Бевза, Апостолової, Єршова та Тарасенкової, продемонструвала, що кожен із них акцентує увагу на різних аспектах викладання.

Особливо важливим є те, що теорема синусів була доведена двома способами: через використання площі трикутника і проведення висоти в довільному трикутнику. Це дозволяє учням бачити різні аспекти теореми та її застосування в практиці. Додатково, теорема косинусів була доведена трьома способами: векторним, координатним і геометричним із використанням висоти трикутника. Це підкреслює гнучкість і універсальність цих теорем у різних ситуаціях.

У процесі роботи також було самостійно доведено три наслідки з теореми синусів та п’ять наслідків із теореми косинусів, що ще більше підтверджує їх практичну значущість для розв’язання задач.

Учні стикаються з низкою проблем при вивченні теорем синусів і косинусів. По-перше, це методичні складнощі: часто викладання зосереджене на формальному виведенні формул без достатньої кількості практичних прикладів, що ускладнює розуміння зв'язку теорем із реальними задачами. Відсутність візуалізації (геометричних рисунків чи інтерактивних платформ) і недостатня кількість вправ для самостійної роботи також негативно впливають на засвоєння матеріалу. По-друге, є психологічні аспекти: страх перед складністю геометрії, відсутність мотивації через нерозуміння практичної цінності теорем, а також стрес від помилок в обчисленнях. По-третє, когнітивні труднощі включають прогалини в базових знаннях (тригонометрія, властивості трикутників), слабке абстрактне мислення і складність вибору правильного методу для розв’язання задач.

Розглянуті теореми синусів і косинусів суттєво розширюють можливості вирішення задач для різних типів трикутників, на відміну від теореми Піфагора, яка обмежується лише прямокутними трикутниками. Це підкреслює важливість детального вивчення цих теорем у навчальних програмах. Порівняння показало, що теореми мають спільні елементи та відмінності в умовах застосування, що ще більше підкреслює їх взаємозв'язок.

Аналіз показав, що підручники, представлені різними авторами, надають різні акценти: наприклад, підручник Мерзляка виділяється своєю наочністю та візуальним супроводом, що полегшує сприйняття абстрактних понять. У той же час, підручники Єршова та Істера акцентують увагу на формальній чіткості, що може бути корисним для учнів, які потребують більш глибокого розуміння теорії. Бевз пропонує практичні приклади, що робить навчання більш актуальним, а Бурда забезпечує учнів великою кількістю завдань для самостійної роботи, що стимулює їх активність. Апостолова, в свою чергу, надає зрозумілі пояснення, що робить матеріал доступним для всіх учнів, незалежно від їхнього рівня підготовки.

Важливо, щоб підручники не лише містили формальні докази, але й пропонували достатню кількість прикладів і завдань для закріплення матеріалу. Інтуїтивне розуміння застосування теорем є ключовим для розвитку математичних навичок. Загалом, аналіз підручників виявив, що найбільш ефективними є ті, які поєднують теоретичні аспекти з практичними завданнями та візуальними поясненнями.

Отже, результати дослідження підтверджують важливість використання різноманітних методичних підходів у навчанні тригонометрії. Це дозволяє врахувати індивідуальні потреби учнів і сприяє більш ефективному засвоєнню теорем синусів і косинусів. На основі отриманих даних можна зробити висновок, що підручники, які поєднують теоретичні аспекти з практичними завданнями та візуальними поясненнями, є найбільш ефективними для навчання учнів 9 класів. Проте залишається актуальною проблема недостатньої інтерактивності та інноваційних методів, що потребує подальших досліджень і вдосконалення освітніх матеріалів. 

 

РОЗДІЛ 2. ГЕОМЕТРИЧНІ ЗАСТОСУВАННЯ ТЕОРЕМИ СИНУСІВ ТА

КОСИНУСІВ

   

Теореми синусів і косинусів є основними інструментами в геометрії, особливо при роботі з трикутниками. Їх застосування охоплює широкий спектр задач, що дозволяє знаходити невідомі сторони та кути трикутників, а також аналізувати їх властивості.

2.1. Розв'язання геометричних задач за допомогою теореми синусів

Задача 1  [4, №507]

Який з кутів трикутника АВС найбільший, а який найменший, якщо: 1) а=6 см, b=8 см, с=7 см; 2)

Дано:,

1)

2)

                                                                                                                       Знайти:  найбільший та найменший кут.

Розв’язання:

В АВС проти більшої сторони лежить  більший кут і навпаки наслідок 2 з теореми синусів.

1)                                                                                                                                     найбільшасторона  найбільший,

 найменшасторона  найменший

2)                                                                                                                                     

3)                                                                                                                                     найбільшасторона  найбільший,

 найменшасторонанайменший.

Відповідь: 1) найбільший, найменший 2) всі кути рівні; 3) найбільший,найменший

Задача 2  

В трикутнику  ABC сторона  ВС = 4 м,  АС . Знайдіть А.

Дано:ВС = 4 м,  АС                

Знайти: А .

 

Розв’язання:

В ⊿АВС затеоремою синусів:

.

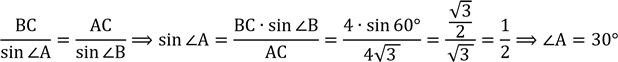Відповідь: 30⁰.

Задача 3 

В трикутнику  ABC сторона  AС =27cм ,  DС =18 см,  ∠В=120⁰. Знайдіть два інші кути трикутника.

Дано: ⊿АВС,

           ВС = 18 см ,  АС = 27см,  ∠В=120⁰

Знайти: ∠А,∠С  .

 

Розв’язання:

В ⊿АВС затеоремою синусів:

 

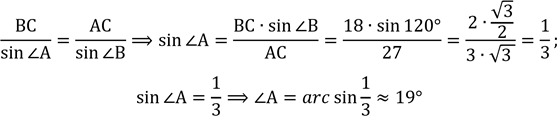
∠С = 180° − (∠А + ∠В)(завластивістюкутівтрикутника);

Отже, ∠С = 180° − (120° + 19°) = 41° Відповідь: ≈ 19° і ≈ 41° .

Задача 4

У  трикутнику b = 8 і c = 5, 𝛽 = 80°. Знайдіть кут, що лежить проти сторони с.

Дано: ⊿: b = 8, c = 5,  𝛽 = 80°. 

Знайти:𝛾. 

                                                                                                 Розв’язання

Затеоремою синусів:

.

Відповідь: 38°.

Задача 5

Сторона трикутника дорівнює 18, а прилеглі кути - 75⁰ і 45⁰ відповідно.

Знайдіть сторону трикутника протилежну до кута 45⁰.

          

А

 Дано: ⊿ABC:

             АВ= 18; ∠А = 75°, ∠В = 45°

^В Знайти: АС  .

С

Розв’язання:

В ⊿ABC проти кута В лежить сторона АС.

∠С = 180° − (∠А + ∠В)(завластивістюкутівтрикутника);

Отже, ∠А = 180° − (45° + 75°) = 60°

                                                                                                          АС             АВ

З  теоремисинусів::

 

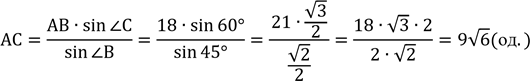
Відповідь ∶ 9√6 од.

Задача 6

      В трикутнику АВС сторона ВС= 3см, градусна міра кутів А та С дорівнюють 60⁰ і 45⁰ відповідно. Знайдіть сторону трикутника, що лежить проти кута С.

          

А

 Дано: ⊿ABC:

             ВС= 3см; ∠А = 60°, ∠С = 45°

^В Знайти: АВ  .

С

Розв’язання:

В ⊿ABC проти кута С лежить сторона АВ.

                                                                                                          АВ             ВС

З  теоремисинусів::

 

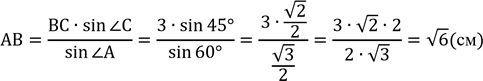
Відповідь:см.

Задача 7 

У трикутнику дано сторону ВС =15 см і прилеглі до неї кути градусна міра яких 85 і 47. Знайдіть невідомі сторони трикутника. 

 

Дано:: ВС =15см;; .

                                                                                                                   Знайти:  АС, АВ .

Розв’язання завластивістюкутівтрикутника)

 

                                                                                                     ВС          АС

Затеоремоюсинусів:

З властивістю пропорції:

                                                                                        ВСВ    

АС см

                                                                                            А         

                                                                                                     ВС          АВ

Затеоремоюсинусів:

З властивістю пропорції:

                                                                                       ВС         С

                                                                          АВ                                                                         см

А

Відповідь:смісм.

Задача 8 [3, №473 стор.120]

Використовуючи дані рисунка знайдіть довжини відрізків АВ, BD, CD, BC.

Дано: рис: AD = 22

          

Знайти: АВ, BD, CD, BC.

 

Розв’язання

Ватеоремоюсинусів:

Звідси:

завластивістюкутівтрикутника)

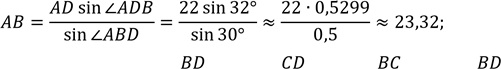
Ватеоремоюсинусів:

,  

завластивістюкутівтрикутника)Маємо : 

Відповідь:.

Задача 9

Знайдіть  радіус кола ,описаного навколо  трикутника одна сторона якого   23 см, а протилежний кут 150⁰. 

Дано:: а23 см;.

Знайти: R.

 

Розв’язання

 

 

.

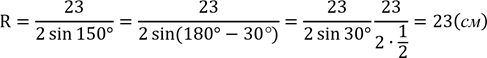Відповідь:.

Задача 10

Сторона трикутника  7,4 см, а протилежний кут їй кут дорівнює 45⁰.

Знайдіть радіус кола ,описаного навколо цього трикутника

Дано: ⊿:

а=7,4 см; 𝛼 = 45°.

Знайти: R.

                                                                                                                          Розв’язання

                                                                                                                                                а                    а

Занаслідкомзтеоремисинусів:

.

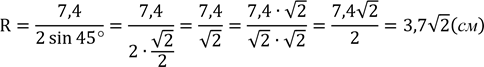Відповідь: 3,7√2 см.

Задача 11

Знайдіть сторону трикутника, якщо радіус кола ,описаного навколо цього трикутника дорівнює 14 см , а кут,протилежний цій стороні, дорівнює 120⁰. 

Дано: ⊿:

R = 14 см;  𝛼 = 120°.

Знайти: а.

 

Розв’язання

а

Занаслідкомзтеоремисинусів:.

а.

Відповідь: 14√3 см.

Задача 12  [2, №574]

Сторона  трикутника відноситься до радіуса описаного навколо

трикутника кола як √2: 1. Знайдіть кут, що лежить проти цієї сторони.

Дано: ⊿:

а :;

Знайти:  𝛼.

 

Розв’язання:

                                                                                                                                                                            а                       а

Занаслідкомзтеоремисинусів:

.

Відповідь: 45°.

Задача 13

Сторона трикутника  см, а протилежний кут їй кут дорівнює 45⁰. Знайдіть сторону трикутника, що лежить проти кута 30⁰ та радіус описаного кола.

Дано: ⊿, а = 7√2  см; 𝛼 = 45°;𝛽 = 30°.

Знайти: b та R.  Розв’язання:

 

 

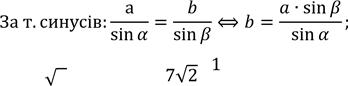
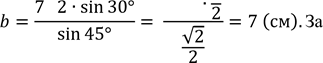наслідкомзтеоремисинусів:

R7(см).

                                                  2 sin 𝛼      2 sin 45              √2

2 ∙

Відповідь: 7смі  7 см.

Задача 14

  У трикутнику ⊿ABC дано АС=9 см, АС=11 см, ∠В = 50° Знайдіть ∠А, ∠С.

Дано: ⊿ABC:   

          АС=9 см, АС=11 см, ∠В = 50°

Знайти: ∠А, ∠С.

 

Розв’язання:

В ⊿АВС затеоремою синусів:

.

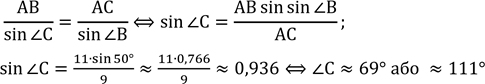∠А = 180° − (∠В + ∠С)(завластивістюкутівтрикутника);

Отже, ∠А = 180° − (50° + 69°) = 61°  або ∠А = 180° − (50° + 111°) = 19°      

Відповідь: ≈ 69°і ≈ 61°або 111°і ≈ 19°

Задача 15

Радіус кола, описаного навколо трикутника ABC, дорівнює 8 см. Знайдіть радіус кола, описаного навколо трикутника AOC, де O — точка перетину бісектрис трикутника ABC, якщо ∠ABC = 120°.

Дано: ⊿АВС,O — точка перетину           бісектрис ⊿ABC;

         R = 8 см; ∠ABC = 120°

            Знайти: R1 . Розв’язання В ⊿АВС занаслідкомзтеоремисинусів:

 

  

∠A+∠С=180°-∠ABC =180°- 120°=60°(завластивістюкутівтрикутника);

Оскільки АО і ОС бісектриси⊿ABC , то

AОС= 180° − 30° = 150°;

АС В⊿АОС за  наслідкомзтеоремисинусів:

 

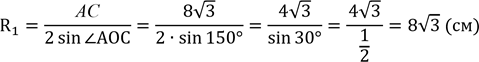
Відповідь: 8√3 см.

Задача 16

Знайдіть радіус кола описаного навколо рівнобедреного трикутника з основою 24 см та бічною стороною 13 см .

Дано: ⊿𝐴𝐵𝐶 − рівнобедрений:

          AC = 24 см; 𝐴𝐵 = 13 см Знайти:  R.  Розв’язання:

 

 

В рівнобедреному ⊿𝐴𝐵𝐶 (𝐴𝐵 = В𝐶 = 13 см − за означенням) проведемо висоту ВК, ВК⊥ АС ⟺ ВК − медіана (за властивістю висоти проведеної до основи).  Звідси маємо АК = КС = 24:2 = 12 (см).

Розглянемо ⊿𝐴𝐵К, ∠К = 90°( ВК- висота),

За теоремою Піфагора:  АВ² = АК² + ВК² ⟺ ВК² = АВ² − АК²

Маємо ВК² = 13² − 12² = 169 − 144 = 25 ⟺ ВК = 5(см) або − 5 < 0- не задовольняє умову задачі.

 

Відповідь: 16,9 см.

Задача 17

У прямокутному трикутнику бісектриса госторого кута ділить протилежний катет на відрізки завдовжки 8 см і 10 см. Знайдіть гіпотенузу трикутника.

Дано: ⊿𝐴𝐵𝐶 − прямокутний:

          CК = 8 см; К𝐵 = 10 см Знайти:  АВ.

 

Розв’язання:  У прямокутному ⊿𝐴𝐵𝐶 ∠С = 90°;

За Наслідком3 про властивість бісектриси, маємо:

 .

Нехай коефіцієнт пропорційності дорівнює x, тоді АС=4х см,а АВ=5х см.

ВС = ВК +СК= 8+10=18(см)

За теоремою Піфагора:  :

 (5𝑥)² = (4𝑥)² + 18² 

25 𝑥² = 16𝑥² + 324

25 𝑥² − 16𝑥² = 324

9 𝑥² = 324

𝑥² = 36 ⟺ 𝓍 = 6 або − 6 < 0 − не задовольняє умову задачі.

Отже, АВ=5𝓍 = 5 ∙ 6 = 30(см)

Відповідь: 30 см.

Задача 18     Навколо рівнобічної трапеції описано коло. Знайдіть його радіус, якщо діагональ трапеції утворює з нижньою основою кут 30º, а бічна сторона дорівнює 7 см.

Дано: ABCD-  рівнобічна трапеція;

         АВ = 7 см - бічна сторона; ∠ВDА = 30°;  Знайти: R. Розв’язання:

 

В ⊿АВ𝐷 занаслідкомзтеоремисинусів:

.

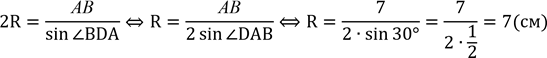Відповідь: 7 см.

Задача 19

Радіус  описанного навколо трапеції кола дорівнює 4√3 дм. Знайдіть довжину її діагоналі, якщо один із кутів трапеції дорівнює120°.

Дано: ABCD – трапеція, 𝐵𝐶 ∥ 𝐴𝐷 ;

          R=4√3 дм; ∠В = 120° Знайти: BD.

 Розв’язання:

 

Якщо навколо трапеції  ABCD можна описати коло , то вона рівнобічна і AC = BD( за властивості).  Коло, описане навколо трапеції  ABCD, описане навколо ⊿𝐴𝐵𝐷.

А тому знайдемо радіус кола описаного навколо ⊿𝐴𝐵𝐷:

∠BAD = 180° − 120° = 60°.  В ⊿АВ𝐷 занаслідкомзтеоремисинусів:

.

Відповідь: 12 см.

Задача 20

Основи трапеції дорівнюють 7 і 23 см, бічна сторона – 17 см. Знайдіть радіус кола описаного навколо трапеції 

Дано:ABCD-  трапеція;

          ВС, АD- основи трапеції; ВС = 7 см; АD = 23 см; АВ=17 см; Знайти:  R.

 

Розв’язання:

Якщо навколо трапеції  ABCD можна описати коло , то вона рівнобічна⟺ АВ = CD(за означенням).  

У трапеції ABCD проведемо ще одну висоту CH ⊥ 𝐴𝐷 ⟺ ⊿АКВ і ⊿СНD- прямокутні.

⊿АКВ = ⊿СНD(за гіпотенузою АВ = CD та катетом CH = 𝐴𝐷) ⟺

 

У прямокутному ⊿𝐴𝐾𝐵 (∠𝐾 = 90°) з теореми Піфагора:

  :

 𝐵К² = 17² − 8² = 289 − 64 = 225;

.

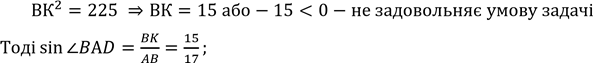У прямокутному ⊿𝐵𝐾𝐷 (∠𝐾 = 90°) за теоремою Піфагора:

  𝐵𝐷² = KD² + ВK², маємо:

 𝐵𝐷² = 15² + 15² = 2 ∙ 15²;

 

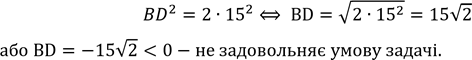
В ⊿АВ𝐷 занаслідкомзтеоремисинусів:

.

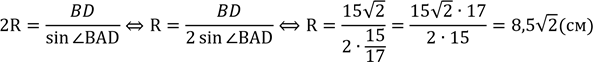 Відповідь: 8,5√2 см.

Задача 21

Знайдіть радіус         кола   описаного   навколо       трапеції       основи        якого дорівнюють 4 і 14 см, а висота 12.

Дано:ABCD-  трапеція;

          ВС, АD- основи трапеції; ВС = 4 см; АD = 14 см; ВК=12 см; Знайти:  R.

 

Розв’язання:

 

Якщо навколо трапеції  ABCD можна описати коло , то вона рівнобічна. 

У трапеції ABCD проведемо ще одну висоту CH ⊥ 𝐴𝐷, 

 

У прямокутному ⊿𝐴𝐾𝐵 (∠𝐾 = 90°) за теоремою Піфагора:

  АВ² = АK² + ВK², маємо: 𝐴𝐵² = 5² + 12² = 25 + 144 = 169;

.

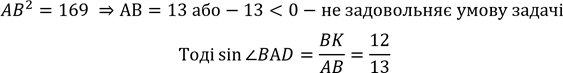У прямокутному ⊿𝐵𝐾𝐷 (∠𝐾 = 90°) за теоремою Піфагора:

  𝐵𝐷² = KD² + ВK², маємо:     𝐵𝐷² = 9² + 12² = 81 + 144 = 225;

𝐵𝐷² = 225; BD = 15 або − 15 < 0 − не задовольняє умову задачі.

В ⊿АВ𝐷 занаслідкомзтеоремисинусів:

.

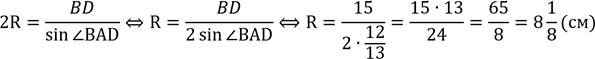 Відповідь: 8,125 см.

Задача 22 [3, №2]

Знайдіть радіус кола, описаного навколо рівнобічної трапеції ABCD, висота якої ВН дорівнює 24 см і ділить більшу основу на відрізки 10 см і 18 см

Дано:ABCD-  рівнобічна трапеція;          ВН = 24 см;АН = 10 см; HD=18 см.

Знайти:  R.

Розв’язання:

 

                                                 Коло, описане навколо трапеції  ABCD, описане навколо⊿𝐴𝐵𝐷.

А тому знайдемо радіус кола описаного навколо ⊿𝐴𝐵𝐷

В ⊿АВ𝐷 занаслідкомзтеоремисинусів:.

У прямокутному ⊿𝐴Н𝐵 (∠Н = 90°) за теоремою Піфагора:

  АВ² = АН² + ВН², маємо:

.

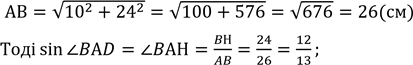У прямокутному ⊿𝐵𝐻𝐷 (∠Н = 90°) за теоремою Піфагора:

  𝐵𝐷² = BН² + 𝐻𝐷², маємо:

 .

Тоді .

Відповідь: 16,25 см.

 

Задача 23

Знайдіть радіус кола, описаного навколо трапеції з основами 3 см і 11 см

та кутом 30° між діагоналлю і бічною стороною.

Дано: ABCD-  рівнобічна трапеція;

           ВС, АD- основи трапеції;

      ВС = 3 см; АD = 11 см ;  ∠АВD = 30°;  

Знайти: R.

 

Розв’язання:

В ⊿АВ𝐷 занаслідкомзтеоремисинусів:

 

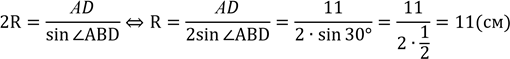
Відповідь: 11 см.

Задача 24

Навколо рівнобічної трапеції описано коло радіуса 13 см. Знайдіть бічну сторону трапеції, якщо  діагональ утворює з нижньою основою кут 30°.

Дано: ABCD-  рівнобічна трапеція;            R = 13 см- радіус описаного кола;    

 ∠АDВ = 30°.  

Знайти: АВ.

 

Розв’язання:

В ⊿АВ𝐷 занаслідкомзтеоремисинусів:

                                                               АВ                                                                                    1

                                     АВ = 2R sin                                                                                                     ADB     = 2   13 sin 30° = 26       = 13    

Відповідь: 13 см.

Задача 25 [6, №9]

        Сума двох сторін трикутника дорівнює 18 см. Знайдіть довжини цих сторін, якщо проти них  лежать кути 30° і 135°.   

Дано: ⊿:            а .

Знайти: a, b.

 

Розв’язання:

Нехай a=х см , тоді b=18-х (см). Затеоремоюсинусів:. Звідси:

                                                         х           18 − х

                                    =                                                                          

 

.

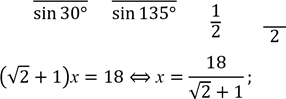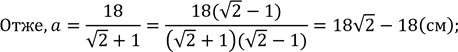
Відповідь:18√2 − 18 смі 36 − 18√2 см.

Задача 26 [6, №10]

 Різниця  двох сторін трикутника дорівнює 4 см. Знайдіть довжини цих сторін, якщо проти них  лежать кути 120° і 45°.  

Дано: ⊿:

          b - a = 4, 𝛼 = 45°, 𝛽 = 120°.

                                                                                                                       Знайти: a, b.

Розв’язання:

𝛽 > 𝛼, бо 120° > 45° ⟺ 𝑏 > 𝑎 (наслідок 2 з теореми синусів); Нехай a=х см , тоді b= 4+х (см).

Затеоремоюсинусів:Звідси: 

                                              х            4 + х          х       4 + х

 ⟺

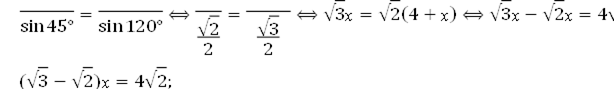х .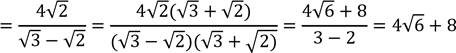

Отже, 𝑎 = 4√6 + 8(см);  𝑏 = 4 + 4√6 + 8 = 4√6 + 12(см).

Відповідь:4√6 + 8смі 4√6 + 12 см.

Задача 27

Знайдіть радіус кола, якщо в ньому хорда завдовжки 17√2 см стягує дугу 135°.

Дано: коло, 

АВ = 17√2 см - хорда; ◡АВ = 135°.

Знайти: R. 

                                                                                                     Розв’язання:

Враховуючи, що центральний кут дорівнює дузі на яку він спирається, маємо:

∠АОВ = ◡АВ = 135°. Розглянемо ⊿АОВ − рівнобедрений(АО = ОВ = 𝑅). 

За наслідком з теореми синусів, маємо:

                                                                                       АВ               17√2              17√2         17√2

R =;

sin ∠

2

Відповідь: 17 см.

Задача 28 [5, №80]

 Радіус  кола, описанного навколо трикутника дорівнює 4 дм. Знайдіть

кути трикутника, якщо дві його сторони дорівнюють 4 см і 4√3 см. Скільки розв'язків має задача?

Дано: ⊿: 

R = 4 дм;  а = 4 см; b = 4√3 см;

Знайти:  𝛼, 𝛽, 𝛾.

 

Розв’язання: R=4 дм=40 см;

Занаслідкомзтеоремисинусів:

 

 

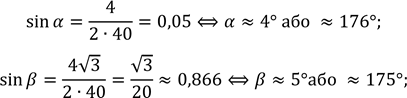
𝛾 = 180° − (𝛼 + 𝛽)(завластивістюкутівтрикутника);

Якщо 𝛼 ≈ 4°, 𝛽 ≈ 5°, то 𝛾 = 180° − (𝛼 + 𝛽) = 180° − (4° + 5°) = 171°

Якщо 𝛼 ≈ 176°, 𝛽 ≈ 5°, то 𝛾 = 180° − (𝛼 + 𝛽) = 180° − (176° + 5°) = −1°

< 0 − незадовольняє умову;

Якщо 𝛼 ≈ 4°, 𝛽 ≈ 175°, то 𝛾 = 180° − (𝛼 + 𝛽) = 180° − (4° + 175°) = 1° Якщо 𝛼 ≈ 176°, 𝛽 ≈ 175°, то 𝛾 = 180° − (𝛼 + 𝛽) = 180° − (176° + 175°)

= −171° < 0 − незадовольняє умову;

Отже, здача має 2 розв’язки.

Відповідь:

Задача 29 [4, №515 стор.88]

Кути трикутника відносяться, як 1: 2:3. Як відносяться його сторони? 

Дано: ⊿АВС, ∠А: ∠В: ∠С = 1: 2: 3;

Знайти:  a : b : c -?                                                   

                                                                                                                        Розв’язання:

Нехай х – коефіцієнт пропорційності , тоді , ∠А = х, ∠В = 2х, ∠С = 3х.

∠А + ∠В + ∠С = 180°, маєморівняння  х + 2х + 3х = 180° ⟺ х = 30°.

Отже,  

                                                                                                        а           𝑏             с

Затеоремоюсинусів:

 sin 30°

                                           а           с                а sin С      а sin 90°      а ∙ 1

= с =        а; sin А sin С sin

а.

Відповідь: 1 ∶ √3: 2.

Задача 30 [4, №516]

У трикутнику АВС а = 12 см, b = 5 см. Чи  може синус ∠В дорівнювати:     1) 0,25  2) 0,5   3)0,7

Дано: ⊿АВС,

           а=12 см, b = 5 см. 

Чи може:  sin В = 1)0,25  2) 0,5   3)0,7

 

Розв’язання:

−1 ≤ sin 𝛼 ≤ 1

                                                                                                                              а           𝑏                            а sin В

  В ⊿АВСзатеоремоюсинусів:.

  

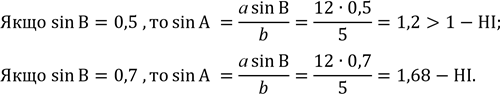
Відповідь: 1) Так   2) Ні   3) Ні.

Задача 31 [4, №524]

       Знайдіть сторони b і c трикутника ABC, якщо a = 8 см, ∠A: ∠В: ∠С = 4: 2: 3.

Дано: ⊿АВС, a = 8 см, ∠A: ∠В: ∠С = 4: 2: 3.

Знайти:  b і c.

 

Розв’язання:

Нехай х – коефіцієнт пропорційності , тоді , ∠А = 4х, ∠В = 2х, ∠С = 3х.

∠А + ∠В + ∠С = 180°, маєморівняння:  4х + 2х + 3х = 180° ⟺ х = 20°.

Отже,  

Затеоремоюсинусів:

                                                                                  а          𝑏                     а sin В     8 sin 40°      8 ∙ 0,6428

 Звідси:       =       ⟺ 𝑏 =           =       ≈         ≈ 5,22; sin А           sin В  sin А  sin 80°          0,9848

                                                                         а           с                а sin С      а sin 60°      8 ∙ 0,866

.

                                                                    sin А      sin С                  sin А       sin 80           0,9848

Відповідь: 5,22 см і 7,04 см.

 

2.2. Розв'язання геометричних задач за допомогою теореми  косинусів

Задача 1

У довільному трикутнику дві сторони 6 см і 8 см утворюють кут 60°.

Знайдіть третю сторону трикутника.

Дано: ⊿ABC:

          АВ=6 см; ВС=8 см; ∠АВС = 60°

Знайти: АС.

                                                                                                                       Розв’язання

В ⊿ABC за теоремою косинусів: 𝐴𝐶² = 𝐴𝐵² + 𝐵𝐶² − 2𝐴𝐵 ∙ 𝐵𝐶 ∙ cos ∠𝐵  

  

Отже, АС=√36 = 6(см)                                                                             

Відповідь: 6 см.

Задача 2

У довільному трикутнику дві сторони 5 дм і 16 дм утворюють кут 120°.

Знайдіть третю сторону трикутника.

                                                          _В                                  Дано: ⊿ABC, АВ = 5 см; ВС= 16 см;

          ∠АВС = 120°

                                                                        _{А С}                             Знайти: АС  .

                                                                             ^?                         Розв’язання

В ⊿ABC за  теоремою косинусів: 𝐴𝐶² = 𝐴𝐵² + 𝐵𝐶² − 2𝐴𝐵 ∙ 𝐵𝐶 ∙ cos ∠𝐵  

361 ⇒ АС  

Відповідь: 19 см.

 

Задача 3

У довільному трикутнику дві сторони 2 см і 3 см утворюють кут 60°.

Знайдіть третю сторону трикутника.

Дано: ⊿ABC:

          АВ=2 см; ВС=3 см; ∠АВС = 60°

Знайти: АС  .

 

Розв’язання

За теоремою косинусів: 𝐴𝐶² = 𝐴𝐵² + 𝐵𝐶² − 2𝐴𝐵 ∙ 𝐵𝐶 ∙ cos ∠𝐵  

 

Відповідь: √𝟕 см

Задача 4

У довільному трикутнику дві сторони 4 см і 6 см утворюють кут 50°.

Знайдіть третю сторону трикутника.

Дано: ⊿ABC:

          АВ=4 см; ВС=6 см; ∠АВС = 50°

Знайти: АС  .

 

Розв’язання

За теоремою косинусів: 𝐴𝐶² = 𝐴𝐵² + 𝐵𝐶² − 2𝐴𝐵 ∙ 𝐵𝐶 ∙ cos ∠𝐵, маємо: 

𝐴𝐶² = 4² + 6² − 2 ∙ 4 ∙ 6 ∙ cos 50° ≈ 52 − 48 ∙ 0,6428 ≈ 21,1462.  

Отже, АС=√21,1462 ≈ 4,6 см.

Відповідь: ≈ 4,6 см

Задача 5

У  трикутнику b °. Знайдіть третю сторону⊿.

Дано: ⊿:            b °. 

Знайти: а.

 

Розв’язання

𝛼 = 180° − (𝛽 + 𝛾)(за властивістю кутів трикутника);

𝛼 = 180° − (80° + 38°) = 62°.

За теоремою косинусів: 𝑎² = 𝑏² + 𝑐² − 2𝑏 ∙ 𝑐 ∙ cos 𝛼, маємо: 

𝑎² = 8² + 5² − 2 ∙ 5 ∙ 8 ∙ cos 62° ≈ 64 + 25 − 80 ∙ 0,6428 ≈ 51,4423.  

Отже, .

Відповідь: ≈ 7,17.

Задача 6

У довільному трикутнику дві сторони 1 см і  7√3 см утворюють кут 150°.

Знайдіть третю сторону трикутника.

Дано: ⊿ABC:

          АВ = 1см; АС =7√3 см; ∠А = 150° Знайти: ∠А. 

 Розв’язання

За теоремою косинусів:ВС² = АВ² + АС² − 2АВ ∙ АС ∙ cos ∠А;  

ВС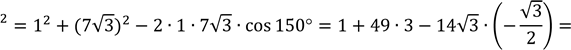

= 148 + 21 = 169 ⇒ ВС=√169 = 13(см).                                            

Відповідь: 13 см.

Задача 7

         В трикутнику  ABC відомо, що 𝑎 = 7 ,  b=10,  ∠С =30⁰. Знайдіть сторону  c.

Дано: ⊿ABC:

          а = 7 см; b = 10 см; ∠С = 30°

Знайти: c.

 

Розв’язання

За теоремою косинусів:𝑐² = 𝑎² + 𝑏² − 2𝑎 ∙ 𝑏 ∙ cos ∠𝐶  

.  

Отже, см

  Відповідь:.

 

Задача 8

У довільному трикутнику сторони дорівнюють  8 см,5 см і 7 см . Знайдіть градусну міру кута, що лежить проти сторони 7 см. 

      

А

 Дано: ⊿ABC:

                                                                                                                  а=8 см;b=7 см;с = 5 см;

                                          В                                                            Знайти: 𝛽.

                                                                       8 см                            С

Розв’язання

                                                                                                                                                               𝑎2 + 𝑐2         𝑏2

                                         Занаслідком 2 зтеоремикосинусів:                                            

  

 

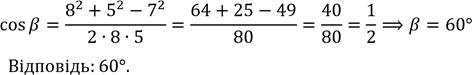
 Задача 9

У довільному трикутнику сторони дорівнюють 7 см,5 см і 6 см . Знайдіть косинус кута А цього трикутника. 

Дано:  ⊿ABC: АВ=7 см; ВС=5 см; АС=6 см Знайти: cos ∠ А.

 

Розв’язання

За теоремою косинусів:𝐵𝐶² = 𝐴𝐵² + 𝐴𝐶² − 2𝐴𝐵 ∙ 𝐴𝐶 ∙ cos ∠𝐴, звідси маємо:

.

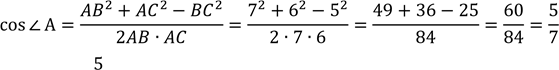Відповідь:.

Задача 10 [2, стор.106]

 Знайти радіус кола, описаного навколо трикутника зі сторонами 5 см,

√7смі2√3см.

 Дано: ⊿:

         𝑎 = 5 см, 𝑏 = √7см, с = 2√3см; Знайти: R.

 

Розв’язання

За теоремою косинусів:𝑏² = 𝑎² + 𝑐² − 2𝑎 ∙ 𝑐 ∙ cos 𝛽,  звідси маємо:

 

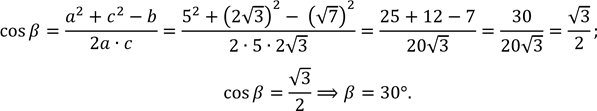
Занаслідкомзтеоремисинусів:

Звідси: R =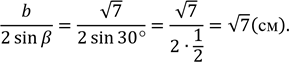

  Відповідь: √7 см.

Задача 11   [5]

      Знайдіть сторони паралелограма, якщо його діагоналі завдовжки 10 см і 16 см перетинаються під кутом 60°.(Є16)

C                                                                Дано: ABCD- паралелограм:

           AC і BD- діагоналі;

          АС = 16  см; BD=10 см;    

D                                                                ∠( BD, AC) = 60°

                                                                                                       Знайти: АВ, BС, CD, AD.

Розв’язання

Розглянемо паралелограм ABCD

 АВ=CD і  ВС=AD (як протилежні сторони паралелограма);

 Нехай діагоналі паралелограма перетинаються в точці О, тобто

 BD ∩ AC = О ⟺ ∠АОВ = 60° 

Оскільки діагоналі паралелограма точкою перетину діляться навпіл , тоАО=ОС=16:2=8 (см), ОВ=OD=10:2=5 (см)

За теоремою косинусів із ⊿АОВ:АВ² = 𝐴О² + ОВ² − 2𝐴О ∙ ОВ ∙ cos ∠𝐴ОВ,  звідси маємо:

АВ,то АВ=7(см).

Скористаємося властивістю сторін та діагоналей паралелограма:

16² + 10² = 2(7² + ВС²);

  256 + 100 = 2(49 + ВС²);

49 + ВС² = 356: 2;

ВС² = 178 − 49;

ВС² = 129 ⟺ ВС = √129(см);

Відповідь:

Задача 12

      Дано паралелограм зі сторонами √10 см і √30 см. Одна з діагоналей паралелограма вдвічі довша за  другу. Знайдіть довжини діагоналей паралелограма.

                                                  B                                 C     Дано:ABCD- паралелограм: BD=2AC

            AC і BD- діагоналі;

           АВ=√10  см; ВС=√30 см;  А D Знайти: АС і  BD.

В паралелограмі ABCD: АВ=DC= √10  см і  ВС=AD= √30 см (як протилежні сторони паралелограма).

Нехай АС=х см, тоді BD=2х (см).

Скористаємося властивістю сторін та діагоналей паралелограма:

 

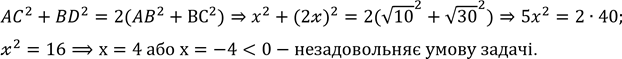
Отже, АС=4 см ,а BD=2 ∙ 4 = 8(𝑐м)

Відповідь: 4 смта 8 см

Задача 13

Одна із сторін трикутника на 10 см менша від  другої ,а кут між цими   сторонами дорівнює 60°. Знайдіть більшу з цих сторін, якщо третя сторона

                                                                                                 Дано:ABC:

В 

           АС більше за АВ на 10 см; 

      14 см             ВС=14 см;  А С        Знайти: АС .

Розв’язання

Нехай АВ = х см, тоді АС = х+10(см)

За теоремою косинусів:, маємо:

х     х        х        х        °   х   х        х        х        х х      х  

За теоремою Вієта: х₂1, х₂-16<0- не задовольняє умову задачі;      Отже, АВ6 см,  АС10+616(см).

Відповідь: 16 см.

Задача 14

Сторони  трикутника, одна з яких на 8 см більша за  другу, утворюють кут 12, а третя сторона дорівнює 28 см. Знайдіть периметр трикутника.

                                        А                                                     Дано:ABC:

           ВС більше за АВ на 8 см; 

                АС = 28 см;  В       С       Знайти: Р -?

Розв’язання

РАВ АС ВС

Нехай АВ = х см, тоді ВС = х+8 (см)

За теоремою косинусів:А В ВВ, тоді:

 ххх х°  

  

х  

                                      х           х                     

                                      х         х                  

За теоремою Вієта:   х₁= - 20 <0 - не задовольняє умову задачі;   х₂= 12

Отже,  АВ = 12 см, ВС = 12 + 8 = 20 (см).

Р_⊿ABC = 12 + 28 + 20 = 60 (см);

Відповідь: 60 см.

Задача 15[11, №202]

У трикутнику АВС відомо, що ∠С = 90°,АС=9 см, ВС=12 см. На стороні АВ позначимо точку D так,що  AD=5 см. Знайдіть довжину відрізка CD. Дано:⊿ABC,  ∠С = 90°; АС = 9 см; ВС=12 см;          D∈ АВ; AD= 5 см.

Знайти: СD. 

                                                                                                        Розв’язання:

Розглянемо⊿ABC- прямокутний (∠С = 90°)

За теоремою Піфагора: 𝐴В² = 𝐴С² + 𝐵𝐶²

𝐴В² = 9² + 12² = 81 + 144 = 225, отже АВ =√225 =15 см.

 

В ⊿ABD за теоремою косинусів: 𝐶𝐷² = 𝐴𝐶² + 𝐴𝐷² − 2𝐴𝐶 ∙ 𝐴𝐷 ∙ cos ∠𝐴.  

 

Відповідь: 2√13 см.

Задача 16 [6, №2]

Знайдіть довжину діагоналі BD чотирикутника ABCD, у якого∠С = 60°.

ВС= 50 мм, CD =35 мм.

Дано:ABCD- чотирикутник,  ∠С = 60°;

          ВС = 50мм; СD= 35 мм;  Знайти: BD.

Розв’язання

В ⊿СBD за теоремою косинусів:ВD² = ВС² + СD² − 2ВC ∙ СD ∙ cos ∠С  

В

1975 ⟹ BD =√1975 = 5√79 мм.   

Відповідь: 5√79 мм.

Задача 17 [6, №12]

 Діагоналі паралелограма дорівнюють 17 см і 19 см, а сторони відносяться як 2:3. Знайдіть периметр паралелограма.

                                                 B                                 C                Дано: ABCD- паралелограм:

            AC і BD- діагоналі; АС = 17 см;

 BD =19 см; AB : BC = 2:3

                                       А                                   D                         Знайти:Р_ABCD

Розв’язання

В паралелограмі ABCD: АВ=DC і  ВС=AD(як протилежні сторони паралелограма); Р_ABCD = 2(АВ + ВС), AB : BC = 2:3 (за умовою)

Нехай х- коефіцієнт пропорційності , тоді АВ =2х см, а BС =3х (см).

Скористаємося властивістю сторін та діагоналей паралелограма:

𝐴𝐶² + 𝐵𝐷² = 2(𝐴𝐵² + ВС²).

  17² + 19² = 2((2х)² + (3х)²).

289 + 361 = 2(4x² + 9x²);

650 = 26𝑥² ∕: 26;

𝓍² = 25 ⟹ х = 5 або х = −5 < 0 − незадовольняє умову задачі

Отже, АВ =2∙х=2∙ 5 = 10 см, а BС =3∙х=3∙ 5 = 15 (см); Р_ABCD = 2(10 + 15) = 50 (см).

Відповідь: 50 см.

Задача 18 [5, №52 стор.19]

Знайдіть сторони паралелограма, якщо його периметр дорівнює 34 см, а діагоналі 11 см і 13 см.

                                               В                         _С   Дано: ABCD- паралелограм, AC і BD- діагоналі;

          АС= 13 см; BD =11 см;Р_ABCD =34 см;   _А D Знайти: АВ, BС, CD, AD. 

Розв’язання

Розглянемо паралелограм ABCD: АВ=DC і  ВС=AD(як протилежні сторони паралелограма); Р_ABCD = 2(АВ + ВС), Р_ABCD = 34 см.

Нехай АВ =х см, тоді ВС = Р_ABCD: 2 − АВ = 34: 2 − х = 17 − х (см).

Скористаємося властивістю сторін та діагоналей паралелограма:

𝐴𝐶² + 𝐵𝐷² = 2(𝐴𝐵² + ВС²).

  13² + 11² = 2(x² + (17 − х)²);  

169 + 121 = 2(x² + 289 − 34х + x²);   290 = 4x² − 64х + 578;

x² − 17 + 72 = 0;    За теоремою Вієта, маємо х₁= 8; х₂= 9 Отже, АВ =DC=8 см,  ВС=AD = 17 − 8 = 9 (см).

Відповідь: 8 см, 9 см, 8 см і 9 см. 

Задача 19[5, №55]

Сторони трикутника завдовжки 10 см і 42 см утворюють кут 120⁰.

Знайдіть довжину медіани, проведеної з вершини даного кута.

                                                                                                  Дано: ⊿ABC:

B

          AВ= 10 см і ВС=42 см; 

     ВК – медіана, ∠АВС = 120°;  А         К       С       Знайти: ВК.

Розв’язання  В ⊿АBС  за теоремою косинусів:

АС² = АВ² + ВС² − 2АВ ∙ ВС ∙ cos ∠АВС, маємо: 

АС²    

За наслідком з теореми косинусів:

 

                                                                                            

Відповідь: 19 см.

Задача 20[6, №18]

Медіана АМ трикутника АВС утворює із стороною ВС кут 60°. Знайдіть

сторону АС, якщо ВС = 32 см, АВ=2√97 см.

Дано: ⊿ABC, AВ= 2√97см і ВС=32 см; 

АМ – медіана, ∠АМВ = 60°;

Знайти: АС.

 

Розв’язання

 В ⊿АBС, АМ = х см – медіана ⟺ ВМ = МС = 32: 2 = 16(см).

В⊿АМВза теоремою косинусів:АВ² = ВМ² + АМ² − 2 ∙ АМ ∙ cos ∠АМВ

388 = 16² + 𝑥² − 2 ∙ х ∙ 16 ∙ cos 60° = 256 + 𝑥² − 16х;  

𝑥² − 16х − 132 = 0;

За теоремою Вієта:  х₁= 22 та х_я= - 6 <0 - не задовольняє умову задачі;

Отже, АМ=22 см.

За наслідком з теореми косинусів:

 

 

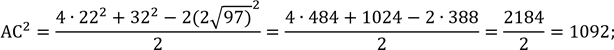
АС = √1092 = 2√273 (см).

Відповідь: 2√273 см.

Задача 21 [1, №4]

Дві сторони  трикутника дорівнюють 23 см і 30 см, а медіана, проведена до більшої з них, дорівнює 10 см. Знайдіть третю сторону трикутника. Дано: ⊿ABC,    AC =23 см, ВС=30 см;           АМ=10 см – медіана.

                                                                                                                                        Знайти: АВ.

Розв’язання

     На продовженні відрізка АМ за точку D відкладемо відрізок МD=AM=10 см.

Тоді AD=20 см.

 У чотирикутнику ABCD діагональ АD і ВС точкою М перетину діляться навпіл (ВМ = МС за умовою,АМ = МD за побудовою). Отже, чотирикутник ABCD – паралелограм. Скористаємося властивістю сторін та діагоналей паралелограма:    𝐴𝐷² + 𝐵𝐶² = 2(𝐴𝐵² + АС²)

  20² + 30² = 2(АВ² + 23²);

400 + 900 = 2(АВ² + 529) ⇒ АВ² = 650 − 529 = 121 ⟹ АВ = 11 (см).

Відповідь: 11 см. 

Задача 22

Медіани AN і CK трикутника АВС перетинаються в точці Р і утворюють кут ∠АРС = 130°. Знайдіть сторону АС, якщо AN = 9 см, а СК= 12 см.

Дано: ⊿ABC,ВС = 50мм; СD= 35 мм;

         AN=9 см і CK=12 см - медіани;         AN ∩ CK = Р,  ∠АРС = 130°. 

                                                                                                                                 Знайти: АС.

Розв’язання:

 (властивістьмедіантрикутника);

                                                             РN      1

Нехай х – коефіцієнт пропорційності , тоді  AР = 2х(см), аРN = хсм.

AN = AР + РN і AN = 9 см(заумовою)

Маєморівняння: 2х + х = 9 ⇒ х = 3.

Отже,РN = 3 см , AР = 2х = 6 (см).

                                      СР     2

                                               =     (властивістьмедіантрикутника).

                                      РК     1

Нехай х – коефіцієнт пропорційності , тоді  СР = 2х (см), аРК = хсм.

СК = СР + РК і СК = 12 см(заумовою).

Маєморівняння: 2х + х = 12 ⇒ х = 4.

Отже,РК = 4 см, СР = 2х = 8 (см).

В ⊿АРСза теоремою косинусів:АС² = АР² + РС² − 2АР ∙ РС ∙ cos ∠АРС; 

АС² = 6² + 8² − 2 ∙ 6 ∙ 8 ∙ cos 130° ≈ 100 − 96 ∙ (−0,6428) ≈ 100 + 61,7 =

161,7 ⇒ АС ≈ √161,7 ≈ 12,7 см   Відповідь: ≈ 12,7 см.

2.3. Задачі для самостійного розв’язування на теорему синусів

 

1)  В трикутнику ABC відомо, що a=7, ∠А = 45°, ∠В = 60°. Знайдіть сторону b.

2)  В трикутнику АВС ∠В = 35°, ∠С = 25°. Вкажіть найбільшу сторону ⊿. 3)Один з кутів трикутника дорівнює 30°, а діаметр кола, описаного навколо трикутника, дорівнює 14 см. Знайдіть сторону, протилежну до даного кута.

4)  В трикутнику  ABC сторона  ВС = 6 м,  АВ . Знайдіть ∠А.

5)  В трикутнику  ABC сторона АВ =14,∠А=60⁰,  ∠С=45⁰. Знайдіть АС, ВС.

6)  В трикутнику  ABC відомо, що сторона  АВ = 12 см, ВС= 10 см,  sin ∠А = 30⁰.

Знайдіть синус кута С трикутника.

7)  Дано рівнобедрений трикутник АВС з основою АС. Відомо,що АС - найменша сторона трикутника. В яких межах може змінюватися величина кута А.

8)  В трикутнику  ABC відомо, що сторона  АС = 9√3 см, ВС= 9 см,  ∠А = 30⁰.

Знайдіть синус кута В трикутника.

9)  Знайдіть радіус описанного навколо трикутника кола, якщо відомо що в ньому протии сторони 2 см  кут: а) 30°; б) 135°; в) 90°. [6, №10]

10)   Радіус  описанного навколо трикутника кола дорівнює √8 дм. Знайдіть довжину сторони, яка лежить проти кута  міри а) 45°; б) 150°; в) 135°. [5, №10] 11) Радіус  кола, описанного навколо рівнобедреного трикутника з кутом 120⁰

дорівнює 8√3 см. Знайдіть сторони трикутника. [5, №79]

12)  Знайдіть радіус кола, описанного навколо рівнобедреного трикутника АВС з основою АС та  кутом при вершині 120°.

13)  Знайдіть радіус кола, описанного навколо рівнобедреного трикутника з основою 16 см і бічною стороною 10 см. [1, №3.22]

14)  Радіус кола, описаного навколо трикутника, дорівнює одній з його сторін.

Знайдіть кут протилежний до даної сторони. Скільки розв’язків має задача. 15)        Сума двох сторін трикутника дорівнює 12 см. Знайдіть довжини цих сторін, якщо проти них  лежать кути 60° і 45°.

16)              Різниця  двох сторін трикутника дорівнює 5 см. Знайдіть довжини цих сторін ,якщо проти них  лежать кути30° і 45°. [10]

17)              Основи рівнобедреної трапеції дорівнюють 9 см і 21 см, а висота 8 см.

Знайдіть радіус кола, описаного навколо трапеції [1, №3.28]

18)              Знайдіть сторони b і c трикутника ABC, якщо a = 6 см, ∠A: ∠В: ∠С =

3: ^[1]: 4. [4, №525]

19)              В паралелограмі ABCD точка М – середина сторони ВС. Відомо, що

∠В −тупий. Порівняй кути MAD і MDA. [5, №84]

20)              Дві сторони трикутника дорівнюють 4 см і √3 см, а третя сторона дорівнює радіусу кола, описаного трикутника. Яку довжину може мати третя сторона?

 

2.4. Задачі для самостійного розв’язування на теорему косинусів

 

1)                Знайдіть невідому сторону трикутника АВС, якщо:

а) АС =25 дм, СВ=50 дм, ∠С = 60°;

б) АС =3,5 м, СВ= 4 м, ∠С = 120°;

в) АС =см,  ВС=6 см, ∠В = 60°;

         г) АС =см, ВС=4 см, ∠В = 135°[6, №1].

2)                Дві сторони трикутника дорівнюють 3 см і 8 см, а кут між ними дорівнює 60°. Знайдіть периметр трикутника.

3)                Одна зі сторін паралелограма на 1 см довша за іншу, а його діагоналі дорівнюють 7 см і 11 см. Знайдіть сторони паралелограма. [2, №541]. 4)          У трикутнику АВС АВ=20 см, АР і BN – медіани трикутника; АР =42 см, BN=36 см. Знайдіть третю медіану трикутника.

6)        З однієї точки кола проведено дві хорди завдовжки 5 см і 8 см. Кінці цих хорд сполучено відрізком, що стягує дугу 120°. Обчисліть довжину цього відрізка, якщо він і задана точка лежать по різні боки від центра кола[6, №15]

7)        З однієї точки кола проведено дві хорди завдовжки 2√2 см і 6 см. Кінці цих хорд сполучено відрізком, що стягує дугу 90°. Обчисліть довжину цього відрізка, якщо він і задана точка лежать: а) по різні боки від центра кола; б) по один бік від центра кола. [6, №17]

8)        Бісектриса АР трикутника АВС утворює з стороною ВС кут 60°. Сторона АС і АВ дорівнюють 6 см і 8 см відповідно. Знайдіть довжину сторони ВС. 9) Знайдіть найдовшу медіану трикутника, сторони якого дорівнюють 7 см,

6 см і √26см.

10) Сторона  трикутника більша за медіану, проведену до неї, на 4 см, а дві інші сторони дорівнюють 28 см і 36 см. Обчисліть периметр трикутника. [6, №24]. 11)Дві сторони  трикутника дорівнюють 6 см і 7 см, а медіана, проведена до меншої з них, дорівнює 5 см. Знайдіть третю сторону трикутника.[6, №17] 12) Дві сторони трикутника дорівнюють 7 см і 9 см, а медіана, проведена до третьої сторони. Відносяться до цієї сторони як 2 : 7. Знайдіть периметр трикутника. [2, №528]

13)              Знайдіть найбільший кут трикутника, якщо:

1)    a = 5 см, b = 3 см, с = 4 см; 2) a = 3 см, b = 4 см, с = 6 см; 

2)    3) a = 40 см, b = 13 см, с = 37 см. [4, №576]

14)              Основи трапеції дорівнюють6 см і 11 см. одна з її бічних сторін дорівнює

8 см й утворює з основою кут 60°. Знайдіть діагоналі трапеції.[4,№581] 15) Бісектриса кута паралелограма ділить його сторону на відрізки завдовжки 5 см. Знайдіть діагональ паралелограма, якщо друга його діагональ дорівнює 9 см. [4, №585]

16)                 У трапеції ABCD AD∥СВ, AD= 8см,  CD= 4√3см. Коло, яке проходить через точки А, В і С, перетинає відрізок АD  в точці К, причому ∠АКВ = 60°.

Знайдіть ВК. [5, №58]

17)                 На сторонах кута, який дорівнює 45°, позначено дві точки, які віддаленні

від вершини кута на 17 см і 12√2 см. Знайдіть відстань між цими точками. 18)     Дві сторони трикутника дорівнюють 3 см і 7 см, а кут, протилежний до більшої з них дорівнює 60°. Знайдітьтретю сторону. Доведіть, що кут, протилежний до третьої сторони, -тупий.

19)              У паралелограмі знайдіть :

а)периметр, якщо діагоналі дорівнюють 11 см і 17 см, а одна із сторін – 13см;

б) діагоналі, якщо їх довжини відносяться як 4 : 7, а сторони дорівнюють 7 см і 9 см. [5, №51]

20)              У трикутнику АВС сторони АВ, ВС і АС дорівнюють 15 см, 13 см і 14 см відповідно. Знайдіть: а)косинус найбільшого та найменшого кутів трикутника; б) проекції сторін АВ і ВС на  пряму АС. [6, №8]

21)              Нехай AD і ВС – основи рівнобічної трапеції АВСD. Доведіть, що 𝐴𝐶² =

𝐴𝐷 ∙ 𝐵𝐶 + 𝐴𝐵². [6, №9]

22)              Основи трапеції дорівнюють 3 см і 8 см. Одна з бічних сторін дорівнює 5 см і утворює з меншою основою кут 120°.Знайдіть: а)діагоналі трапеції; б) площу трапеції. [6, №11] 

23)              Трикутник зі сторонами 6 см,10 см і 14 см вписано в коло. Знайдіть центральний кут, який відповідає вписаному куту, утвореному двома меншими сторонами трикутника.

24)              Дві сторони трикутника дорівнюють 7 см і 9 см. Медіана, проведена до третьої сторони, на 1 см менше цієї сторони. Знайдіть периметр трикутника.

 

2.5. Методичні рекомендації щодо покращення подання теорем синусів і косинусів школярам.

1.         Інтерактивні методи навчання- використання інтерактивних геометричних програм (наприклад, GeoGebra) дозволяє учням візуалізувати трикутники, змінювати їх параметри та спостерігати за змінами в співвідношеннях сторін і кутів, що сприяє глибшому розумінню теорем.

2.         Практичні приклади- наводьте реальні життєві ситуації, де застосування теорем синусів і косинусів є необхідним. Наприклад, розрахунок висоти будівлі або відстані до недоступних об’єктів. Це робить матеріал більш актуальним і цікавим.

3.         Поступове введення теми- розпочніть з простих трикутників, таких як прямокутні, і поступово переходьте до довільних трикутників, пояснюючи, як теореми синусів і косинусів розширюють можливості вирішення задач. 4. Візуальні матеріали - використання схем, малюнків і графіків, щоб проілюструвати докази теорем і їх застосування. Яскраві та зрозумілі візуальні матеріали допоможуть учням краще засвоїти матеріал.

5.         Групова робота - заохочуйте учнів працювати в групах над розв'язанням задач. Це стимулює обговорення, обмін ідеями та допомагає учням глибше зрозуміти тему через колективний підхід.

6.         Демонстраційні експерименти - проведення практичних експериментів або використання моделі для демонстрації теорем. Наприклад, вимірювання кута і сторін у трикутнику за допомогою транспортира та лінійки.

7.         Інтеграція з іншими темами - пов’язуйте теореми синусів і косинусів з іншими математичними концепціями, такими як вектори або площі фігур, щоб показати їх широке застосування.

8.         Зворотний зв’язок - регулярно перевіряйте знання учнів через контрольні роботи, тести або усні відповіді, щоб виявити труднощі та коригувати навчальний процес.

9.         Завдання для самостійного розв’язування -  розробіть різноманітні задачі для самостійної роботи, які охоплюють як прості, так і складні випадки, щоб учні могли практикуватися в застосуванні теорем.

10.     Мотиваційні моменти - заохочуйте учнів за успішне виконання завдань та участь у дискусіях. Нагороди, похвала або додаткові бали можуть підвищити їхню мотивацію.

 

 

 

Висновки до розділу 2

Теореми синусів і косинусів забезпечують потужні методи для розв’язання геометричних задач, розширюючи можливості аналізу трикутників у різних конфігураціях. Їх вивчення дозволяє застосовувати знання для вирішення реальних завдань, таких як проектування конструкцій, розрахунок траєкторій у фізиці чи визначення геометричних параметрів в астрономічних спостереженнях.

У другому розділі було детально розглянуто, розв’язано та оформлено 31 задачу, пов’язану із застосуванням теореми синусів, і 22 задачі, засновані на теоремі косинусів. Кожна з них демонструє практичне застосування цих теорем у трикутниках та різноманітних геометричних конфігураціях. Теорема синусів використовується для трикутників, у яких відомі дві сторони та протилежний кут, або два кути й одна сторона, що робить її незамінною для задач, де трикутник не є прямокутним. Теорема косинусів є універсальним інструментом, який дозволяє розв’язувати трикутники будь-якої форми та з будь-яким набором вихідних даних.

Для самостійного опрацювання було запропоновано 20 задач на основі теореми синусів і 24 задачі для теореми косинусів. Це забезпечує учням можливість закріпити теоретичні знання, розвинути аналітичне мислення та вдосконалити точність обчислень. Вирішення таких задач вимагає логічного підходу й розуміння взаємозв’язків між сторонами та кутами трикутника.

Самостійна робота над цими задачами сприяє глибокому розумінню суті теорем, розвитку практичних навичок і здатності застосовувати їх у реальних ситуаціях. Це формує ключові навички, необхідні для майбутніх фахівців у багатьох галузях, і розширює межі використання математики в міждисциплінарних задачах.

Таким чином, теореми синусів і косинусів залишаються важливими математичними інструментами, які дозволяють вирішувати широкий спектр задач, розвивають точність і логіку, а також демонструють, як теоретичні знання застосовуються у практичних ситуаціях.

ВИСНОВКИ

 

 

Розв'язування трикутників є однією з ключових тем шкільного курсу геометрії, яка має важливе значення для розвитку математичних навичок учнів. Теореми синусів і косинусів, що використовуються для вирішення трикутників, займають центральне місце в навчанні геометрії, оскільки дають учням можливість розв'язувати не лише геометричні задачі, а й застосовувати отримані знання в інших галузях науки та техніки.

Дослідження підходів до викладання розв'язування трикутників показало важливість використання різних методів навчання для забезпечення глибокого розуміння теоретичних основ і розвитку практичних навичок учнів. Одним із головних викликів є досягнення балансу між теоретичним викладом матеріалу та його практичним застосуванням. Підручники, які поєднують теоретичне обґрунтування з широким набором практичних завдань, значно підвищують ефективність навчання і сприяють кращому засвоєнню матеріалу.

Окремо важливою є роль інтерактивних методів навчання, таких як використання динамічних програм для візуалізації трикутників, що дозволяє учням краще розуміти та застосовувати теореми синусів і косинусів. Використання таких інструментів у поєднанні з традиційними методами навчання допомагає підвищити інтерес учнів до математики і зробити процес навчання більш захоплюючим та доступним.

Також, важливим аспектом є індивідуалізація навчального процесу, яка враховує різний рівень підготовки учнів. Різнорівневі завдання та диференційований підхід дозволяють кожному учню працювати відповідно до його можливостей, що забезпечує рівномірний розвиток математичних компетентностей. Це, в свою чергу, дозволяє покращити результати вивчення та засвоєння складних математичних концептів.

Рекомендації, розроблені в межах цієї роботи, можуть бути корисними для вчителів, методистів та авторів підручників, оскільки сприятимуть покращенню процесу викладання теми «Розв'язування трикутників». Вони дозволяють враховувати сучасні методи навчання, що підвищують ефективність засвоєння матеріалу учнями різних рівнів підготовки та сприяють розвитку їхніх навичок самостійного розв'язування задач.

У підсумку, результати дослідження підкреслюють необхідність інтеграції сучасних технологій у навчальний процес і розробки нових підходів до викладання розв'язування трикутників, що дозволить створити динамічне та інтерактивне навчальне середовище для учнів. Майбутні дослідження повинні зосередитися на покращенні методик навчання тригонометрії з урахуванням індивідуальних потреб учнів, а також на подальшому вдосконаленні використання сучасних технологій для забезпечення глибокого розуміння і застосування теоретичних знань на практиці.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1.         Геометрія: підруч. для 9 кл. загальноосвіт. навч. закладів / А.Г. Мерзляк, В.Б. Полянський, М.С. Якір. Х.: Гімназія, 2021. -255 с. : іл. 

2.         Геометрія: підруч. для 9 кл. загальноосвіт. навч. закладів /

О.С.Істер.- Київ: Генеза, 2022. -239 с. : іл. 

3.         Геометрія: підруч. для 9 кл. загальноосвіт. навч. закладів / Г.П. Бевз, Н.Г. Владімірова.- К: Видавничий дім «Освіта», 2022. -271 с. : іл. 

4.         Геометрія: підруч. для 9 кл. загальноосвіт. навч. закладів / М.І.Бурда.,Н.А. Тарасенкова.- К.: УОВЦ «Оріон», 2022. -223с. : іл. 

5.         Геометрія: підруч. для 9 кл. загальноосвіт. навч. закладів 2-ге видання / А.П. Єршова,В.В. Глободько,О.Ф.Крижановський,  С.В.Єршов.- Харків: Вид-во «Ранок», 2022. -256 с. : іл. 

6.         Геометрія: 9: дворів. підруч. для загальноосвіт. навч. закл.

/Г.В.Апостолова.- Г.: Генеза, 2009. -304 с. : іл.

7.         Геометрія: підруч. для 7-9 кл. загальноосвіт. навч. закладів 2-ге видання /Атанасян Л.С., Бутузов С.Б. та ін./  – М.: Просвітництво, 2014- 383 с. : іл.

8.         Захарійченко Ю.О. Математика: Зб. тестових завдань для підготовки до зовнішнього незалежного оцінювання / Ю.О. Захарійченко, О.В.

Шко- льний. – К.: Генеза, 2008. – 104 с.

9.         Збірник завдань для державної підсумкової атестації з математики.

Геометрія. 11 клас / За ред. З.І. Слєпкань. – Харків: Гімназія, 2006.

10.    Олійник Л.І., Геометричний тренажер. 9 клас.Тернопіль: Підручники і посібники, 2011.-160с

11.    Геометрія: 7- 9 клас. Практичний довідник / уклад. Чекова Г.Ю.- Чернігів: КММЕДІА 2015. -192 с. 

12.    Науково-методичний журнал Математика в школах України №32(224) листопад 2008р.  https://postou.wixsite.com/mysite/single-post/2016/06/13 -добірка

задач практичного змісту