Самостійна робота "Додавання і віднімання векторів"

Уч._________________________________

Самостійна робота “Вектор. Додавання та віднімання векторів”

Варіант 1

1.Що таке вектор у просторі?

A) Точка у просторі.                   B) Величина з напрямом і величиною.

C) Площина у просторі.             D) Лінія у просторі.

2.Як обчислити суму двох векторів?

A) Додати їхні координати.

B) Перемножити їхні координати.

C) Відняти один вектор від іншого.

D) Знайти модуль кожного вектора.

3.Як обчислити різницю двох векторів?

A) Відняти від першого вектора другий.

B) Перемножити їхні координати.

C) Додати їхні координати.

D) Знайти модуль кожного вектора.

4.Що означає, якщо сума векторів дорівнює нульовому вектору?

A) Вектори перпендикулярні.

B) Вектори однакові за модулем.

C) Вектори протилежно напрямлені.

D) Вектори лежать на одній прямій.

5.Якщо вектори a і b такі, що a + b = b + a, це означає, що вони є:

A) Колінеарними.              B) Перпендикулярними.

C) Рівними.                          D) Протилежно напрямленими.

6.Які з наведених векторів є рівними?

A) (1, 2, 3) і (3, 2, 1)                 B) (0, -1, 1) і (0, 1, -1)

C) (1, -1, 0) і (-1, 1, 0)               D) (2, 1, 0) і (-2, -1, 0)

Завдання 7- 9 оцінюються по 2 б.

7.Знайдіть суму векторів a = (2, -1, 3) і b = (1, 4, -2).

8.Знайдіть різницю векторів c = (-3, 5, 2) і d = (4, -1, 0).

9.Дано  вектори    і  .  Від  точки  А  побудувати 

    .              

Уч.___________________________________________________

Самостійна робота “Вектор. Додавання та віднімання векторів”

Варіант 2:

1.Вектор у просторі характеризується:

A) Тільки величиною.                B) Тільки напрямом.

C) Величиною та напрямом.      D) Ні величиною, ні напрямом.

2.Як обчислити суму векторів у просторі?

A) Додати їхні складові.

B) Помножити їхні складові.

C) Відняти один вектор від іншого.

D) Знайти модуль кожного вектора.

3.Якщо сума двох векторів дорівнює нульовому вектору, то це означає, що вони:

A) Паралельні.                                         B) Рівні за величиною.

C) Протилежно напрямлені.                   D) Лежать на одній прямій.

4.Від чого залежить різниця двох векторів?

A) Від їхнього напряму.

B) Від їхньої величини.

C) Від їхніх складових.

D) Від модуля кожного вектора.

5.Якщо вектори a і b такі, що a + b = b + a, це означає, що вони:

A) Колінеарні.    B) Перпендикулярні.

C) Рівні.               D) Протилежно напрямлені.

6.Яка з операцій неприпустима для векторів у просторі?

A) Додавання вектора до точки.

B) Перемноження векторів.

C) Знаходження модуля вектора.

D) Ділення вектора на число.

Завдання 7- 9 оцінюються по 2 б.

7.Знайдіть суму векторів a = (-1, 2, 3) і b = (4, -3, 1).

8. Знайдіть різницю векторів c = (2, 5, -3) і d = (-4, 1, 6).

9. Дано  вектори    і  .

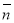 Від  точки  А  побудувати 

    .