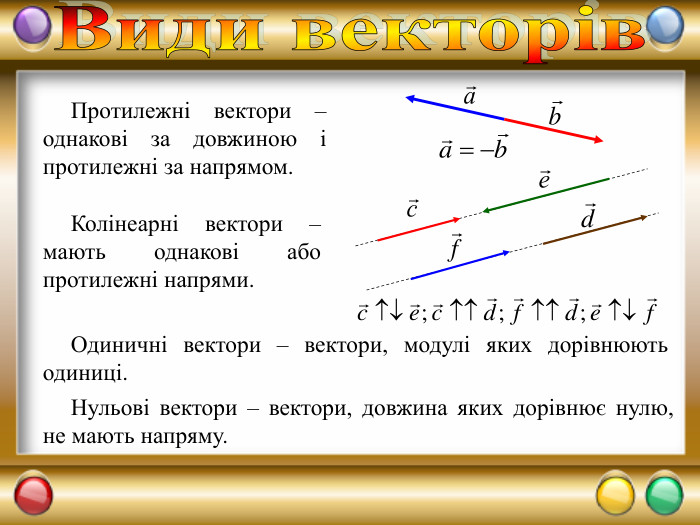
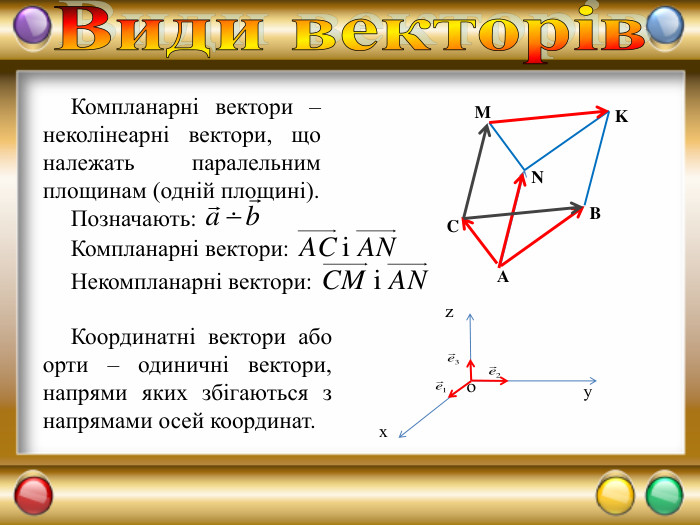
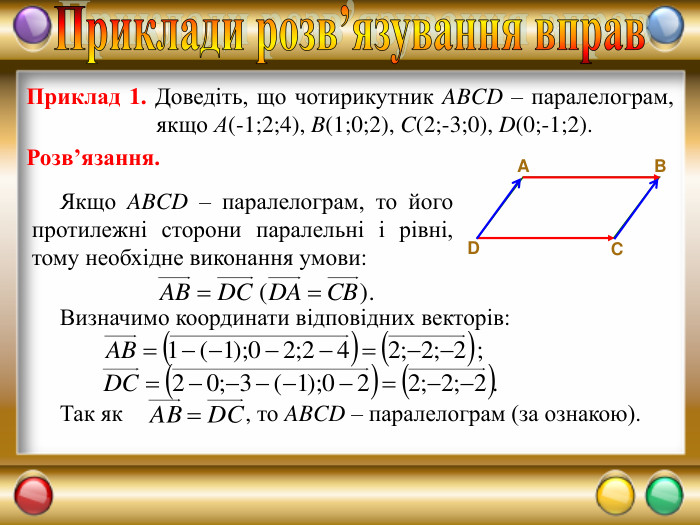
презентація "Вектори у просторі"
Про матеріал
містить теоретичні відомості, приклади розв'язування завдань та кілька завдань на закріплення Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку