Самостійна робота "Вектор. Координати вектора"

Самостійна робота «Вектор. Координати вектора»

І варіант

1. Як визначити координати вектора АВ (х;у) з початком А(х₁;у₁) і кінцем В (х_2; у₂)

А  х=х₂-х₁ ; у=у₁-у₂         Б  х=х₂-х₁; у=у₂-у₁      В  х=х₁-х₂ ; у= у₁-у₂   Г  х=х₁-у₁; у=у₂-х₁

2. Рівні вектори мають

          А  рівні скалярні добутки                       Б  відповідно рівні модулі   

          В  відповідно рівні координати              Г  рівні довжини

3. Ненульові вектори які лежать на паралельних прямих або на одній прямій називають

А  паралельними    Б  перпендикулярними      В  рівними      Г  колінеарними

4. Знайдіть координати вектора АВ, якщо А(2;3), В(-1;4)

           А  (3;1)      Б  (1;3)        В  (-3;1)         Г  (3;3)

5. Дано точки А(3;-7), В(4;-5), С(5;8) D(х;у) .Знайдіть х та у ,якщо АВ=СD

А  (2;2)         Б  (1;1)         В  (6;6)           Г  (3;3)

6. Від точки А(4;-3) відкладено вектор ṁ (-1;8).Знайдіть координати кінця вектора

А  (2;2)         Б  (-1;-1)        В  (4;9)         Г  (3;5)

7. Знайдіть модуль вектора а (3;-4)

А  -2             Б  2               В  -5            Г  5

8. Модуль вектора а(х;-8) дорівнює 10.Знайдіть х

А  4;-4        Б  6;-6         В  3;-3          Г  5;-5

9. Модуль вектора с дорівнює 2, а його координати рівні. Знайдіть координати

вектора с.

          А  (; ) або(-;- )           Б  (; ) або(-;- )

          В  (; )або(-;- )            Г  (; )або(-;- )

10. Знайти довжину вектора ВС, якщо В(10;3), С(-2;-2)

А  169           Б  13            В   119           Г  -13

11. Дано координати трьох вершин паралелограма АВСD А(3;-2), В(-4;1), С(-2;-3). Знайдіть координати вершини D

А  (5;-6)       Б  (5;6)         В  (4;3)        Г  (2;3)

12. Установіть відповідність між початком і кінцем(1-4) та координатами вектора (А-Д)

1    вектор АВ, якщо А(-2;7) і В(3;-3)                 А  (-5;2)

2    вектор КМ, якщо К(-4;5) і М(-9;7)                Б  (5;-1)

3    вектор ВС, якщо В(10;-3) і С(-6;8)                В  (5;-10)

4    вектор РК, якщо Р(-1;-2) і К(4;-3)                  Г  (11;-16)

                                                                                Д  (-16;11)

Самостійна робота «Вектор. Координати вектора»

ІІ варіант

1. Вектор - це...  

А  пряма        Б  відрізок          В  промінь            Г  напрямлений відрізок

2. Модуль вектора-це...

А  модуль координат       Б  довжина відрізка, що зображує вектор

В  довжина відрізка         Г  точки початку і кінця

3. Які з наведених прикладів є векторними величинами?

А  вартість товару      Б  маса     В  довжина      Г  прискорення

Д  час       Е  швидкість      Є  сила     Ж  температура

4. Як називаються два ненульові вектори, які лежать на паралельних прямих або на одній прямій?

А  рівні        Б  співнапрямлені         В  колінеарні        Г  протилежнонапрямлені

5. Якщо початок і кінець вектора одна й та сама точка, він називається...

А  колінеарним      Б  перпендикулярним      В  рівним

 Г  нульовим         Д  одиничним          Е  протилежним

6. Укажіть неправильне твердження 

А  Одиничний вектор - вектор, довжина якого дорівнює 1

Б  Нульовий вектор - вектор, початок і кінець якого збігаються

В  Вектори, які мають однакові довжини, але протилежно напрямлені - протилежні

Г  Протилежні вектори - це протилежно напрямлені вектори

7. Співнапрямленими векторами називають

А  вектори, які рівні за абсолютною величиною

Б  колінеарні вектори, які мають рівні модулі

В  колінеарні вектори, які мають однаковий напрямок

8. Як називаються два ненульові вектори, які мають рівні модулі і є співнапрямленими?

А  колінеарними     Б  компланарними    В  рівними   Г  співнапрямленими

9. Вектор позначають

А  двома великими літерами        Б  двома малими літерами

В  однією великою літерою          Г  однією малою літерою

10. Як знайти координати вектора АВ ?

А  А̅В (х_А+у_А; х_В+у_В)      Б  А̅В (х_А-у_А; х_В-у_В)     В  А̅В (х_В - х_А; у_В - у_А)

Г  А̅В (х_А - х_В; у_А - у_В)

11. Знайдіть координати вектора АВ, якщо А(- 4 ; 3), В ( - 2 ; -1)

А  ( -6; 2)        Б  ( - 2; 4)        В  ( - 1; - 3)          Г  ( 2; - 4)

12. Знайти довжину вектора с̅ (-3; 4)

А  1               Б  7               В  25                  Г  5

13. Дано вектор a̅(4; у). Знайти у, якщо 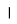a⃓̅ = 5

А  1               Б  3               В  -3               Г  3 або -3

14. Оберіть правильний варіант формули для обчислення модуля вектора 

а̅ (а₁ ; а_2; )

А           Б               В                          Г