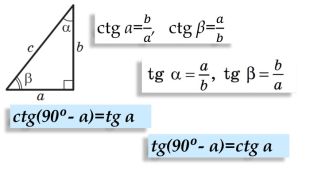
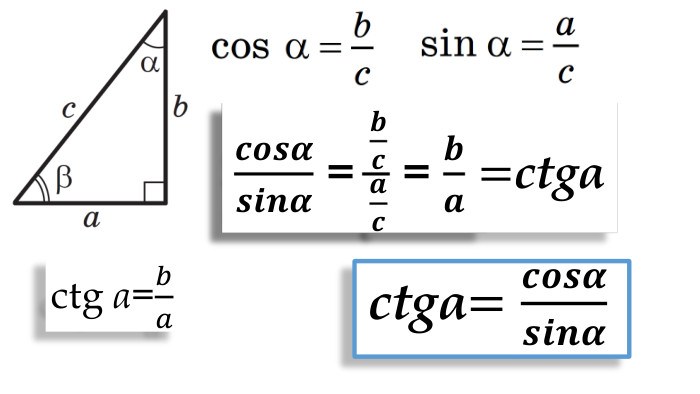Синус, косинус, тангенс гострого кута прямокутного трикутника-2
Про матеріал
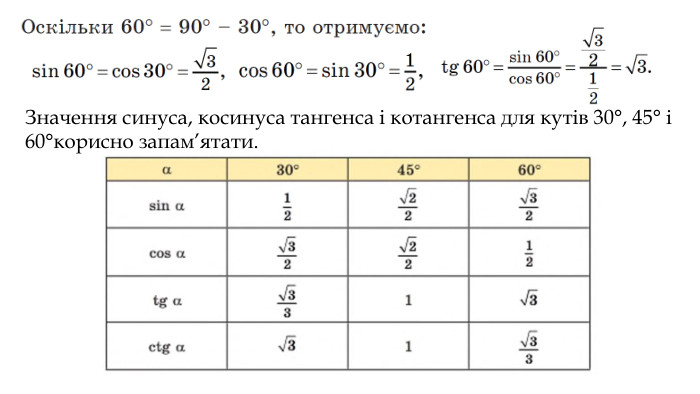
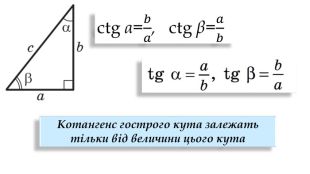
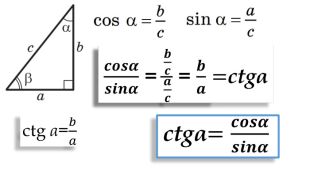
Цей матеріал є допоміжним при вивчення тригонометричних співідношень для прямокутного трикутника. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку