Смарт урок "Величина кута. Вимірювання та побудова кутів"

Тема. Величина кута. Вимірювання та побудова кутів.

Мета: ознайомити з одиницею виміру кутів, з будовою транспортира, сформувати вміння вимірювати та будувати кути за допомогою транспортира.

Тип уроку: засвоєння нових знань, умінь, навичок.

Наочність і обладнання: мультимедійний проектор, інтерактивна дошка, комп’ютер, креслярські прилади, підручник, індивідуальні картки, комп’ютерна презентація «Величина кута. Вимірювання та побудова кутів».

Хід уроку

І. Перевірка домашнього завдання.

Перевірка домашнього завдання заданого за підручником.

Опитування учнів:

1. Що називається кутом?
2. Що називають стороною кута?
3. Що називають вершиною кута?
4. Як позначається кут?
5. Який кут розгорнутий, гострий, тупий, прямий?

Ми з вами повторили основні поняття, тепер до дошки вийде два учні на завдання «Скажені перегони». (Слайд 1)

ІІ. Актуалізація опорних знань. (Слайд 2, 3)

ІII. Вивчення нового матеріалу.

Відкрийте зошити, запишіть число 6 грудня, к.р.. Сьогодні ми продовжимо вивчати кути і темою уроку буде «Величина кута. Вимірювання та побудова кутів». (Слайд 4)

План вивчення теми:

1. Ознайомлення з одиницею виміру кутів.
2. Ознайомлення з будовою транспортира.
3. Правило вимірювання кутів за допомогою транспортира.
4. Правило побудови кутів за допомогою транспортира.
5. Поняття бісектриси кута.

Ознайомлення з одиницею виміру кутів.

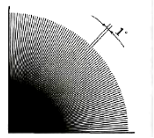Рис. 1

Кути, як і відрізки, можна вимірювати. Поділимо прямий кут на 90 рівних частин (рис. 1). Міру однієї такої частини беруть за одиницю вимірювання кутів і називають градусом. Позначають так: 1°. (Слайд 5)

Градусна міра прямого кута дорівнює 90°, а розгорнутого – 180°. Градусну міру кута позначають так само, як і кут. Це записують так: ∠AOB = 90°. (Слайд 6)

Зрозуміло, що градусна міра гострого кута менша від 90°, а тупого – більша за 90°, але менша від 180°. (Слайд 7)

Заповнимо останній рядок таблиці, яку ми будували на попередньому уроці. (Слайд 8)

На закріплення цього матеріалу усно виконують вправи. (Слайд 9)

Ознайомлення з будовою транспортира.

Кути в градусах вимірюють за допомогою приладу, який називається транспортиром. Шкала транспортира розміщена на півколі і має 180 поділок. Кожна поділка шкали дорівнює 1°. (Слайд 10)

Правило вимірювання кутів за допомогою транспортира.

Перегляд відео (Слайд 11)

На закріплення цього матеріалу усно виконують вправи. (Слайд 12, 13)

Правило побудови кутів за допомогою транспортира. (Слайд 14)

Правило з книжки ст. 148.

Міри кутів, як і довжини відрізків, можна додавати й віднімати. На малюнку ∠MON  дорівнює сумі кутів ∠KON і ∠МОK . Якщо ∠MON = 110°, ∠KON = 40°, то щоб знайти градусну міру кута МОК, потрібно ∠МОK = ∠MON – ∠KON = 110° – 40° = 70°. (Слайд 15)

На закріплення цього матеріалу виконують вправи. (Слайд 16)

Поняття бісектриси кута. (Слайд 17)

Промінь ОK ділить кут АОВ на два рівні кути. Такий промінь називається бісектрисою кута.

Промінь, який виходить з вершини кута і розбиває його на два рівні кути, називається бісектрисою кута.

ОK – бісектриса кута АОВ. ∠AОK = 45°. Знайди ∠AОВ.

∠AОВ = ∠AОK ∙ 2 = 45° ∙ 2 = 90°.

V. Підсумок уроку.

Кросворд (Слайд 18).

VI. Домашнє завдання. (Слайд 19)

§20, ст. 146-149, № 669, 674, 682.