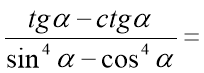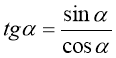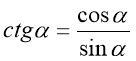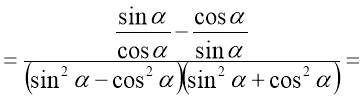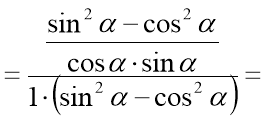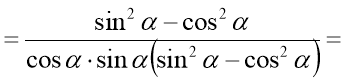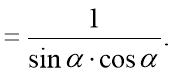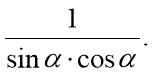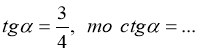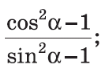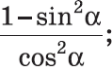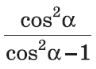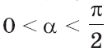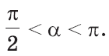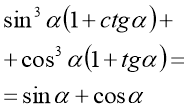Співвідношення між тригонометричними функціями одного аргументу.
Методична розробка розрахована на те, щоб розширити знання учнів про тригонометричні функції; ознайомити з формулами, що пов'язують тригонометричні функції одного й того самого аргументу, формувати вміння і навички застосовувати вивчені співвідношення для тотожних перетворень (спрощення) виразів, знаходження значення тригонометричних функцій за однією відомою функцією.
Тема уроку: Співвідношення між тригонометричними функціями одного аргументу.
Мета уроку:
Навчальна: розширити знання учнів про тригонометричні функції; ознайомити з формулами, що пов'язують тригонометричні функції одного й того самого аргументу, формувати вміння і навички застосовувати вивчені співвідношення для тотожних перетворень (спрощення) виразів, знаходження значення тригонометричних функцій за однією відомою функцією.
Розвивальна: розвивати вміння самостійно міркувати, аналізувати та використовувати набуті знання на практиці; пізнавальний інтерес, логічне мислення,математичну мову, спостережливість, увагу, інтелектуальні здібності.
Виховна: виховувати вміння проводити об’єктивну самооцінку, самостійність та відповідальність, толерантне ставлення учнів до людей; формувати систему моральних ставлень особистості до світу.
Очікувані результати
Учні повинні знати:
- формули подвійного та половинного аргументу;
- як отримувати формули подвійного аргументу з формул додавання;
- як отримувати формули подвійного аргументу з формул додавання.
Учні повинні вміти:
- пояснювати, яку залежність виражають формули подвійного та половинного аргументу;
- отримувати формули подвійного аргументу з формул додавання;
- отримувати формули половинного аргументу з формул подвійного аргументу;
- розв’язувати задачі з даної теми;
- застосовувати отримані знання на практиці.
Тип уроку: засвоєння нових знань і умінь.
Міжпредметні зв’язки: біологія, інформатика, історія, фізика, спецтехнологія, виробниче навчання.
Обладнання уроку: підручники, роздатковий матеріал, ноутбук, мультимедійний проектор та екран,презентація.
План проведення уроку:
- Означення перпендикулярних прямих.
- Ознака перпендикулярності площин.
- Побудова площини, перпендикулярної до заданої.
- Приклади перпендикулярних площин на відповідних моделях або в навколишньому середовищі.
Структура уроку
|
1. |
Організаційний момент |
1 хв |
|
2. |
1. Перевірка домашнього завдання. Актуалізація опорних знань учнів |
5 хв |
|
3. |
Мотивація навчальної діяльності учнів |
2 хв |
|
4. |
Повідомлення теми і мети уроку |
2 хв |
|
5. |
Сприйняття й засвоєння учнями навчального матеріалу |
20 хв |
|
6. |
Закріплення матеріалу. Тренувальні вправи (за рівнями) |
10 хв |
|
7. |
Підсумки уроку |
1 хв |
|
8. |
Оцінювання навчальних досягнень учнів |
2 хв |
|
9. |
Домашнє завдання. Інструктаж до д/з. |
2 хв |
Хід уроку
І. Організаційний момент.
Привітання, налаштування учнів на роботу на уроці.
ІІ. Перевірка домашнього завдання. Актуалізація опорних знань учнів
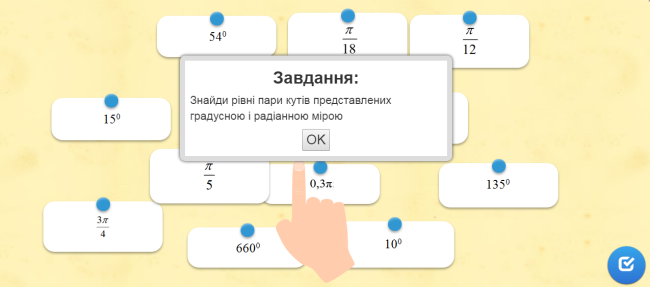
Учні виконують інтерактивні вправи «Знайти рівні пари кутів представлених градусною і радіанною мірою», «Тригонометричні означення».

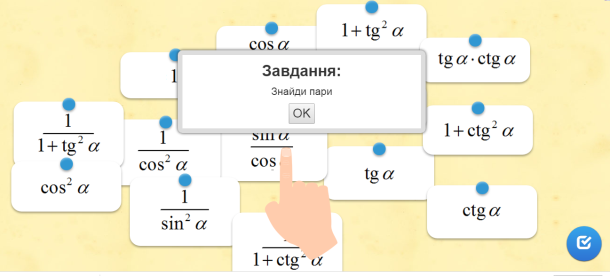
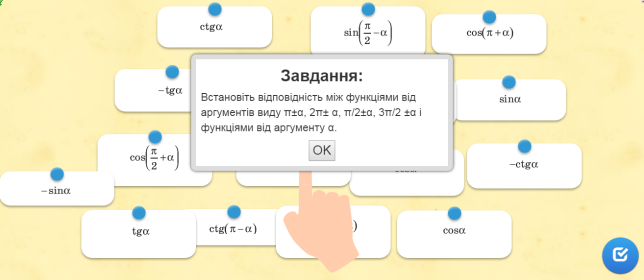
ІІІ. Мотивація навчальної діяльності учнів.
Дуже часто при розв'язуванні задач виникає проблема: знайти значення тригонометричних функцій, якщо задано лише значення однієї з них. Отже, на сьогоднішньому уроці ми повинні згадати формули (залежності), які пов'язують тригонометричні функції одного і того самого аргументу.
ІV. Повідомлення теми і мети уроку. Працювати ми з вами будемо за планом. Запишіть його в зошит

V. Сприйняття й засвоєння учнями навчального матеріалу



Користуючись цими формулами, можна числове значення будь-якої тригонометричної функції виразити через значення іншої тригонометричної функції такого самого аргументу. Але треба враховувати, якій чверті належить цей аргумент.

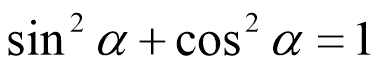


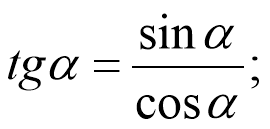
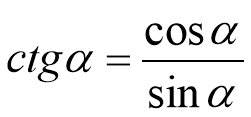

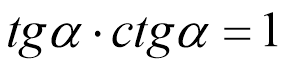


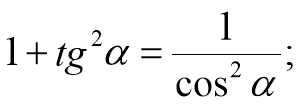
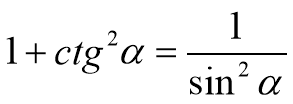
1. Співвідношення між синусом і косинусом.
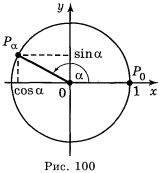 Нехай точка Ρα(х, у) одиничного кола отримана поворотом точки Р0(1; 0) на кут α радіан, тоді згідно з означенням синуса і косинуса: х = cos α, у == sin α (рис. 100)
Нехай точка Ρα(х, у) одиничного кола отримана поворотом точки Р0(1; 0) на кут α радіан, тоді згідно з означенням синуса і косинуса: х = cos α, у == sin α (рис. 100)
Оскільки точка Рα(х;у) належить одиничному колу, то координати (х; у) задовольняють рівнянню х2 + у2 = 1. Підставивши в це рівняння замість х і у значення cos α і sin α , отримаємо:
(cos α)2 + (sin α)2 = 1 або (враховуючи, що (cos α)2 = cos2 α, (sin α)2 = sin2 α)) cos2 α + sin2 α = 1.
Таким чином, sin2 α + cos2 α = l для всіх значень α. Ця рівність називається основною тригонометричною тотожністю.
З основної тригонометричної тотожності можна виразити sin α через cos α і навпаки. ![]() ,
, ![]() .
.
Виконання вправ
1. Чи можуть бути справедливими одночасно рівності:
a) cosα = ![]() і sinα =
і sinα = ![]() ; б) sinα = -
; б) sinα = -![]() і cosα = -
і cosα = -![]() ; в) sinα =
; в) sinα = ![]() і cosα = -
і cosα = - ![]() .
.
при одному і тому самому значенні α?
Відповідь: а) ні; б) так; в) так.
2. Знайдіть cos α, якщо sin α = 0,6 і ![]() < α < π.
< α < π.
Відповідь: cos α = -0,8.
3. Знайдіть sin α, якщо cos α = ![]() і
і ![]() < α < 2π.
< α < 2π.
Відповідь: sin α = -![]() .
.
4. Спростіть вирази:
а) 1 + sin2 α + cos2 α; б) 1 – sin2 α – cos2 α; в) 2sin2 α + cos2 α – 1;
г) (1 – cos α)(l + cos α); д) ![]() ; є) sin4 α – cos4 α + 1.
; є) sin4 α – cos4 α + 1.
Відповідь: а) 2; 6) 0; в) sin2 α; r) sin2 α; д) tg2α; є) 2sin2α.
5. Доведіть тотожності:
а) (1 – cos 2α)(l + cos 2α) = sin2 2α; 6) cos4 α – sin4 α = cos2 α – sin2 α;
в) (sin2 α – cos2 α)2 + 2cos2α sin2α = sin4 α + cos4 α;
r) 2cos2α sin2α + cos4α + sin4α = 1; д) sin6 α + cos6 α = 1 – 3sin2α cos2α;
є) ![]() .
.
6. Знайдіть cos α, якщо cos4 α – sin4 α = ![]() .
.
Відповідь: cosα = ±![]() .
.
2. Співвідношення між тангенсом і котангенсом.
![]() ,
, ![]() .
.
Перемноживши ці рівності, одержимо
![]()
Отже, tgα · ctgα = l для всіх значень α, крім α = ![]() , k, k
, k, k ![]() Ζ. із одержаної рівності можна виразити tg α через ctg α і навпаки:
Ζ. із одержаної рівності можна виразити tg α через ctg α і навпаки: ![]() ;
; ![]() .
.
Виконання вправ
1. Чи можуть бути справедливими одночасно рівності:
a) tg α = ![]() і ctgα =
і ctgα = ![]() ; б) tgα =
; б) tgα = ![]() і ctgα =
і ctgα = ![]() ; в) tg α = -
; в) tg α = - ![]() і ctg α = 2
і ctg α = 2
при одному і тому самому значенні α?
Відповідь: а) так; б) ні; в) ні.
2. Знайдіть
а) tg α, якщо ctg α = ![]() ; б) ctg α, якщо tg α = -1; в) tg α, якщо ctg α = 0.
; б) ctg α, якщо tg α = -1; в) tg α, якщо ctg α = 0.
Відповідь: а) ![]() ; б) -1; в) не існує.
; б) -1; в) не існує.
3. Дано: х = 2tg α, у = ctg α. Знайдіть ху.
Відповідь: ху = ![]() .
.
4. Дано tg α + сtg α = 2. Знайдіть tg 2 α + сtg2 α.
Відповідь: 2.
5. Спростіть:
а) tg α · сtg α – 1; б) sin2 α – tg α · сtg α; в) tg 1° · tg 3° · tg 5° · ... · tg 89°.
Відповідь: а) 0; б) – соs α; в) 1.
6. Доведіть тотожності:
а) (tg α + сtg α)2 - (tg α - сtg α)2 = 4; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
є) 4 + (сtg α - tg α)2 = (сtg α + tg α)2.
3. Співвідношення між тангенсом і косинусом, котангенсом і синусом.
Розділимо ліву і праву частину рівності sіn2 α + соs2 α = 1 на соs2α, вважаючи, що соs2α ≠ 0, одержимо:
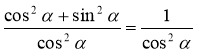 ;
; 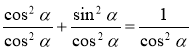 ,
,
звідси: ![]() , де
, де ![]() .
.
Розділимо ліву і праву частину рівності sіn2 α + соs2 α = 1 на sіn2 α, вважаючи, що sіn α ≠ 0, одержимо
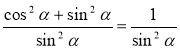 ;
; 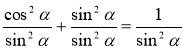 ,
,
звідси: ![]() , де
, де ![]() .
.
Виконання вправ______________________________
1. Чи можуть бути справедливими одночасно рівності.
а) tg α = ![]() і соs α =
і соs α = ![]() ; б) сtg α = 1 і sіn α =
; б) сtg α = 1 і sіn α = ![]() ; в) tg α =
; в) tg α = ![]() і sіn α =
і sіn α = ![]() при одному і тому ж значенні α?
при одному і тому ж значенні α?
Відповідь: а) ні; б) так; в) ні.
2. Відомо, що tg α = 2 і ![]() . Знайдіть sіn α, соs α і сtg α.
. Знайдіть sіn α, соs α і сtg α.
Відповідь: sіn α = ![]() ; соs α =
; соs α = ![]() ; сtg α =
; сtg α = ![]() .
.
3. Відомо, що sіn α = ![]() і 0 < α <
і 0 < α < ![]() . Знайдіть соs α, tg α, сtg α.
. Знайдіть соs α, tg α, сtg α.
Відповідь: соs α = ![]() ; tg α =
; tg α = ![]() ; сtg α =
; сtg α = ![]() .
.
4. Відомо, що сtg α = -3 і α — кут IV чверті. Знайдіть sіn α, соs α, tg α.
Відповідь: sіn α = ![]() ; соs α =
; соs α = ![]() ; tg α =
; tg α = ![]() .
.
5. Відомо, що соs α = ![]() і α — кут І чверті. Знайдіть sіn α, tg α, сtg α.
і α — кут І чверті. Знайдіть sіn α, tg α, сtg α.
Відповідь: sіn α = ![]() ; tg α =
; tg α = ![]() ; сtg α =
; сtg α = ![]() .
.
6. Спростіть вираз:
а) 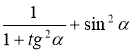 ; б)
; б) 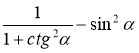 ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
Відповідь: а) 1; б) 0; в) 0; г) 0; д) ![]() ; є) tg α.
; є) tg α.
7. Доведіть тотожності:
а) ![]() ; б) (1 – сtg α)2 + (1 + сtg α)2 =
; б) (1 – сtg α)2 + (1 + сtg α)2 = ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
VI. Закріплення матеріалу.
![]()
Приклад 1. Знайдіть cos α, tg α, ctg α, якщо sin α=0,8 i 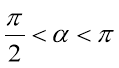 .
.
Розв’язання
![]() , тому
, тому ![]() .
.
Тоді ![]() .
.
α – кут ІІ чверті, тому ![]() .
.
Значить ![]() .
.
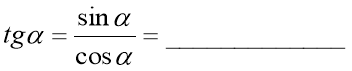 .
.
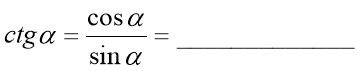 .
.
Відповідь: cos α=___, tg α=___, ctg α=___.
Приклад 2. Спростіть вираз: 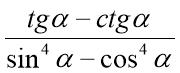 .
.
|
Алгоритм розв’язання |
Розв’язання
|
|
|
|
|
1. Замінимо тангенс і котангенс відношеннями: А вираз у знаменнику розкладемо як різницю квадратів:
|
|
|
2. Зводимо дроби у чисельнику до спільного знаменника |
|
|
3. Ділимо дріб у чисельнику на знаменник |
|
|
4. Скорочуємо дріб
|
|
|
|
Відповідь: |
|
|
І варіант |
ІІ варіант |
Кількість балів |
||
|
|
Початковий рівень |
|
|||
|
1 |
Укажіть неправильну формулу: |
1 |
|||
|
|
А) |
Б) |
В) |
Г) |
|
|
2 |
Чи можуть бути одночасно справедливими рівності: |
1 |
|||
|
|
|
|
|
||
|
3 |
Якщо |
Якщо |
1 |
||
|
|
А) |
Б) |
В) |
Г) |
|
|
|
Середній рівень |
|
|||
|
|
Спростіть вираз: |
|
|||
|
4 |
|
|
1,5 |
||
|
5 |
|
|
1,5 |
||
|
Достатній рівень |
|||||
|
6 |
Знаючи, що |
3 |
|||
|
|
|
|
|
||
|
Високий рівень |
|||||
|
|
Доведіть тотожність: |
|
|||
|
|
|
|
3 |
||
VII. Підсумки уроку Вправа «Мікрофон» .


- Сьогоднішній урок був для мене корисним, тому що ….
- Я дізнався …
- Я навчився …
- Мені сподобалось …
- Мені не сподобалось …
VIII. Оцінювання учнів. Оцінювання навчальних досягнень учнів
(з обґрунтуванням кожного виставленого балу відповідно до Критеріїв оцінювання).
IX. Домашнє завдання. Інструктаж до д/з.
Оголошення домашнього завдання ( обов’язкове та на вибір), інструктаж до його виконання.
Середній рівень
- Спростіть вираз:
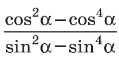
Достатній рівень
- Знайдіть значення:
![]()


- Бевз Г.П. Математика: 10 кл.: підруч. для загальноосвіт.навч. закл. : рівень стандарту / Г.П. Бевз, В.Г. Бевз. – К.: Генеза, 2010. – 320 с.
- А.Г.Конфорович. Добрий день. Архімеде! Цікаві задачі. Ігри, головоломки. – К. Молодь, 1988
- ДПА + ЗНО. Математика. Навчальний посібник О.С. Істер. Генеза- 2013
ЗНО за 30 днів. Математика. Навчальний посібник для підготовки до ЗНО
- Шарыгин И.Ф., Гордин Р.К. Сборник задач по геометрии. 5000 задач с ответами. // Москва, «Астрель», 2001// 396 стор.
- Вишенський В.А., Ганюшкін О.Г., Капташов М.В., Михайловський В.І., Призва Г.Й., Ядренко М.Й., Українські математичні олімпіади. // Київ, «Вища школа», 1993// 415 стор.
-
Дякую за корисний для мене урок! Усі формули в одному місці, алгоритми розв'язування конкретних задач, самоперевірка за допомогою LearningApps - супер!

про публікацію авторської розробки
Додати розробку