Способи розв'язування фізичних задач

Про матеріал

Математика допомагає обчислити основні характеристики фізичних процесів. Особливу роль можна відвести похідній функції та обчисленню інтегралу. Ці математичні формули використовуються для знаходження кінематичних характеристик руху тіл, значень роботи, енергії, потенціалу електричного поля, енергії магнітного поля, інтенсивності світла та багатьох інших фізичних величин. Обчислення за отриманими формулами можна здійснити за допомогою програми Exсel, яка суттєво полегшує завдання з підрахунку та аналізу різних даних у таблицях. Потрібно лише встановлювати формули.

Перегляд файлу

Міністерство освіти та науки України

Синельниківський професійний ліцей

Зміст

ВСТУП

РОЗДІЛ 1

ТЕОРЕТИЧНІ ВІДОМОСТІ З МАТЕМАТИКИ

РОЗДІЛ 2

ФІЗИЧНІ ОСНОВИ МЕХАНІКИ

2.1. Рівноприскорений рух

2.2. Рух тіла, кинутого під кутом до горизонту

2.3.Механічні коливання

2.4. Робота змінної сили

РОЗДІЛ 3

ЕЛЕКТРОМАГНЕТИЗМ

3.1. Електричний струм

3.2. Електромагнітні коливання

РОЗДІЛ 4

ЯДЕРНА ФІЗИКА

ВИСНОВКИ

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ ІНФОРМАЦІЇ

ВСТУП

Тема: Способи розв’язування фізичних задач.

Мета: Порівняти зручність фізичного та математичного методів розв’язування фізичних задач. Дослідити як, користуючись формулами і правилами диференціювання та інтегрування, можна знаходити основні характеристики фізичних процесів і явищ, які можна обчислити за формулами в програмі Microsoft Excel.

Практичне значення: Робота познайомить Вас з фізичним (знаходження фізичних закономірностей для обчислення шуканої величини) і математичним способами (використанням формул знаходження похідної функції та інтегралу при обчисленні величин різних фізичних процесів) та обчисленням фізичних величин в програмі Microsoft Excel.

Дослідницькі завдання:

вивчити літературу з даного питання;
дослідити використання апарату вищої математики (формули похідних та інтегралу) при виведенні фізичних закономірностей;
порівняти зручність фізичного та математичного методів розв’язування фізичних задач;
провести обчислення за формулами в програмі Microsoft Excel;
познайомитися з методами розв’язування прикладних задач.

Структура дослідження: Робота складається з вступу, чотирьох розділів, висновку, списку використаних джерел інформації.

Від живого спостереження до абстрактного мислення

і від нього до практики – це шлях пізнання

істини, пізнання об’єктивної реальності.

Всесвіт, який оточує нас, матеріальний: він складається з матерії, яка знаходиться у неперервному русі. Під рухом матерії розуміють всі зміни та перетворення енергії, всі процеси, які відбуваються у природі. Різні форми матерії досліджуються різними природничими науками, в тому числі і фізикою. Фізика вивчає загальну форму руху матерії: механічні, гравітаційні, електромагнітні, атомно-молекулярні, ядерні процеси. Предмет дослідження фізики містять загальні закономірності явищ природи.

Обчислення за отриманими формулами можна здійснити за допомогою програми Exсel, яка суттєво полегшує завдання з підрахунку та аналізу різних даних у таблицях. Потрібно лише встановлювати формули.

У своїй роботі я намагаюсь порівняти зручність фізичного та математичного методів розв’язування фізичних задач з використанням інформаційних технологій.

РОЗДІЛ 1

ТЕОРЕТИЧНІ ВІДОМОСТІ З МАТЕМАТИКИ

Похідною функції у=f(x) в точці Х₀ називається границя відношення приросту 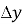функції до приросту 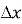аргументу за умови, що приріст 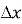аргументу прямує до нуля, а границя існує, тобто

f' (x₀) = =

Механічний зміст похідної: миттєва швидкість нерівномірного руху є похідною від шляху S = f^’ (t), тобто υ = S^’ = f^’ (t).
Прискорення є похідною від швидкості, тобто a = υ^‘ = S^” = f^”(t)
Інтеграл – це обернена дія диференціювання

, де F(x) – первісна функції, С- постійна

$I:\Install\For stady\КАРТИНКИ от Рекотова\шкільна тематика\BD05094_ - копия.WMF$

РОЗДІЛ 2

ФІЗИЧНІ ОСНОВИ МЕХАНІКИ

2.1. Рівноприскорений рух

Найпростішим видом руху матерії є механічний, який характеризується переміщенням в просторі тіл, або їх частин, один відносно одного.

Згідно механічного змісту похідної: миттєва швидкість є похідною від переміщення: υ = S’_t , а прискорення є похідною від швидкості: a = υ’_’t.

Отже, розглянемо розв’язування задач двома способами: фізичним і математичним.

Розв’яжемо задачу із застосуванням похідної.

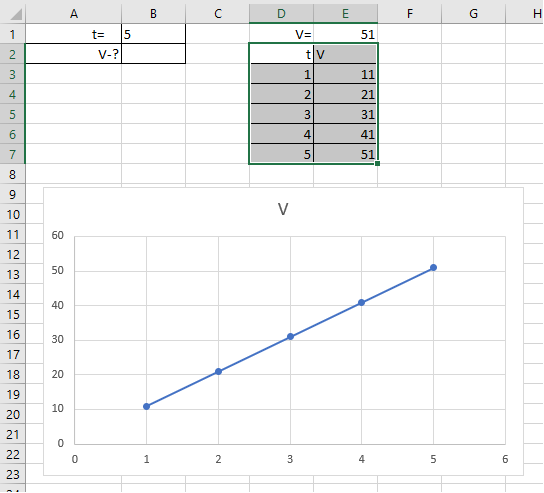
Задача 1

Нехай точка рухається так, що закон її руху виражено формулою

S = 5t²+ t + 2. Визначити: 1) миттєву швидкість точки через 5с;

2) прискорення тіла; 3)зробити графік залежності υ від t для рівноприскореного руху в програмі Excel.

Фізичний метод

Дано: Розв’язок

S = 5t²+ t + 2 За умовою задачі: переміщення обчислюється за

Знайти: формулою S = 5t²+ t + 2.

υ_x- ? З фізики відомо: переміщення тіла при рівномірному

a_x- ? русі обчислюється за формулою:S= υ_{0 x} t + a_xt²/2

Отже, υ_0x= 1 м/c; a_x= 10 м/с²;

υ_x = υ_0x + a_xt = 1 + 10∙5 = 51 м/с

Відповідь: 1 м/с; 10 м/с²; 51 м/с.

Математичний метод

Швидкість рівноприскореного руху є похідною від шляху, отже

υ(5) = S (t) = (5t²+ t + 2)’ = 10t + 1;

υ (5) = S(5) = 10∙5 + 1 = 51 (м/с)

а = υ (t) = (10t + 1)’ = 10 (м/с²)

Відповідь: 10 м/с²; 51 м/с.

Для побудови графіку треба використати формулу =D3*10+1 у комірку E3 =D3*10+1 та скопіювати її E3:E7.

$C:\Users\VladK\OneDrive\Рабочий стол\атестация\Скріни\1.png$

Розглянемо розв’язок задач із застосуванням інтегралу:

Задача 2.
Тіло рухається прямолінійно зі швидкістю, яка змінюється за законом υ = 2t + 1. Знайти шлях, який пройшло тіло за інтервал часу від t₁= 1c до t₂= 3c.

Фізичний метод

За умовою задачі швидкість змінюється за законом υ = 2t + 1.

Дано: Розв’язок:

t₁= 1c Підставимо у формулу t₁= 1c і t₂= 3c.

t₂= 3c. υ₀(t₁) = 2∙1 + 1 = 3 м/с;

υ = 2t + 1 υ (t₂) = 2∙3 + 1 = 7 м/с.

S - ? Прискорення обчислюється за формулою а = ;

Підставимо значення змінних: а = = 2 а = = 2 ².

Переміщення тіла при рівноприскореному русі: S = (υ² – υ₀²)/2а.

Підставимо у формулу значення швидкості і часу: S = .

Перевіримо одиниці вимірювання:

[S] = (м/с)²/ (м/с²)= м²/с² ∙ с²/м = м

Відповідь: 10 м.

Математичний метод

З математики відомо, що переміщення – це первісна від швидкості за певний інтервал часу: S = .

S = 2t + 1)dt =

Відповідь: 10 м.

Задача 3.

На яку максимальну висоту піднімається тіло, яке кинули вертикально вгору зі швидкістю, яка змінюється за законом . Час підйому 3с. зробити розрахунок в Excel.

Фізичний метод

Дано: Розв’язок:

Згідно умові задачі .

t₂ = 3c Швидкість при рівноприскореному русі змінюється за законом:

g = 10 отже м/с, м/с².

h - ? Висоту, на яку піднімається тіло, обчислюємо за формулою:

Підставимо значення початкової швидкості і часу:

h = 20∙3 –

Перевіримо одиниці вимірювання h:

h =

Відповідь: 15м.

Математичний метод

З математики відомо, що

h = = 20∙3 – 5∙3² – (20∙0 –

– 5∙0²) = 60 – 45 = 15 (м)

Відповідь: 15 м.

Для розрахунку h треба використати формулу e rjvshws E1 =20*B2-B3*B2^2/2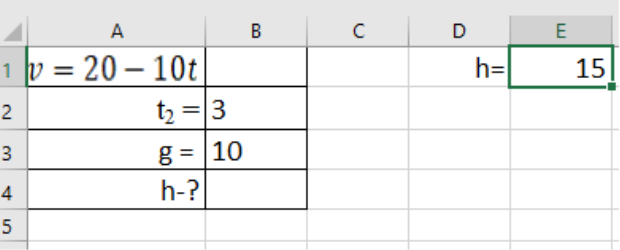

Задача 4.

Матеріальна точка масою 3 кг рухається вздовж осі Ох внаслідок дії сили F. У момент часу t сила F(t) = 2t – 1. Знайти закон руху x = x(t), якщо відомо, що коли t = 1 c, швидкість руху точки 5 , а координата х = 3, де F – сила у ньютонах, t – час у секундах, х – шлях у метрах.

Розв’язок: Використаємо знання з фізики і математики.

За другим законом Ньютона, F = ma. Звідси

Оскільки швидкість є первісною для прискорення руху точки , то

Щоб знайти С₁, врахуємо, що коли t = 1c, швидкість дорівнює 5 . Підставляючи ці значення у рівняння , звідки С₁= 5. Підставляючи С₁ в те саме рівняння, знайдемо закон зміни швидкості

Закон руху x = x (t) є первісною для швидкості. Тому .

За умовою, коли t = 1, то х = 3. Підставляючи ці значення в останнє рівняння, знаходимо 3 = . Звідси С₂ = -.

Підставляючи С₂ в те саме рівняння, дістанемо закон руху .

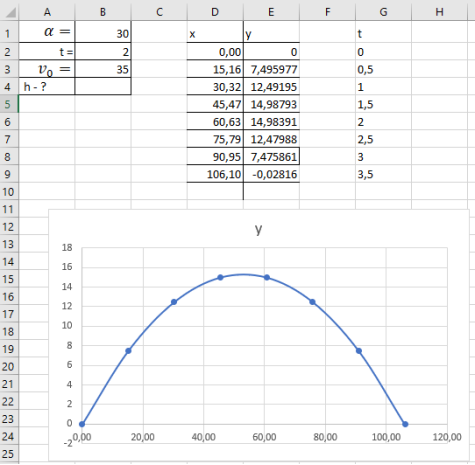
2.2. Рух тіла, кинутого під кутом до горизонту

Задача 5

Снаряд вилетів з гранати під кутом до горизонту з початковою швидкістю Знайдіть висоту піднімання тіла через 2с. В програмі Excel побудувати траєкторію руху тіла кинутого під кутом до горизонту

Фізичний метод

Дано: Розв’язок:

t = 2c

h - ? x

;

h = .

h = 35

Перевіримо одиниці вимірювання:

∙с + ∙ = м.

Відповідь: 15м.

Математичний метод

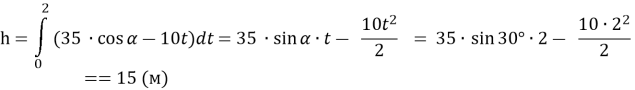
Відповідь: 15 м.

Для побудови графіку у стовбець x: треба ввести формулу =B3*G2*COS(3,14/6), стовбець y: =B3*G3*SIN(3,14/6)-(10*G3^2)/2.

2.3.Механічні коливання

Розглянемо коливання тіла на пружині. Коли ми розтягнемо пружину і відпустимо її, то під дією сили пружності тіло рухається, утворюючи механічні коливання.

Як ми вже знаємо .

Тому рівняння, яке описує коливання тіла на пружині можна записати: де .

Якщо х змінюється за законом:

;

або .

Розв’яжемо задачу 6: На горизонтальному стержні знаходиться вантаж масою 4кг. Вантаж прикріплений до пружини, жорсткість якої 225 . Інший кінець прикріплений. В деякий момент часу вантаж зміщують від положення рівноваги на 10 см і відпускають. Знайти координату вантажу, проекції його швидкості і прискорення через періода коливань. Тертя не враховувати.

Дано: Розв’язок:

m =4 кг Залежність координати груза від часу визначається так:

k= 225

t = Т Так як то

0,1м .

х - ? - ? а -? Проекція швидкості ;

Проекція прискорення

Відповідь:

2.4. Робота змінної сили

Нехай тіло, що розглядається як матеріальна точка, рухається під дією змінної сили F(x), напрямленої вздовж осі Ох. Знайдемо формулу для обчислення роботи при приміщенні з точки у точку х = в.

Нехай А(х) – робота при переміщенні тіла з точки а у точку х. Надамо х приросту . Тоді – робота, яка виконується силою F(x) при переміщені тіла з точки х у точку х +. Коли силу F(x) на відрізку [x; x + вважатимемо сталою, що дорівнює F(x). Тому , звідки

Тоді ,

або , за означенням похідної,

Остання рівність означає, що А(х) є первісною для функції F(x). Тоді за формулою Ньютона-Лейбніца оскільки A(a) = 0.

Отже, робота змінної сили F(x) при переміщені тіла з точки а в точку в дорівнює

А =

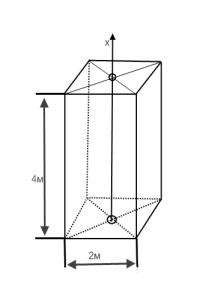Задача 7. Обчислити роботу, яку треба виконати, щоб викачати воду з ями глибиною 4 м, що має квадратний переріз із стороною 2 м. Густина води

Дано: Розв’язок:

g = 10

А-?

Спрямуємо вісь Ох вздовж діючої сили. Значення сили F(x), що діє на переріз прямокутного паралелепіпеда площею 4м², визначають вагою шару води, що знаходиться вище від цього перерізу. Отже, F(x) = 4, де

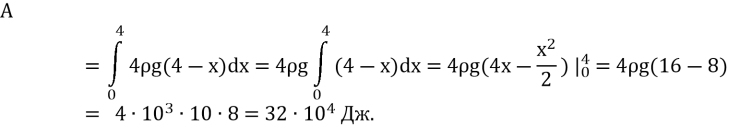
Відповідь:

РОЗДІЛ 3

ЕЛЕКТРОМАГНЕТИЗМ

3.1. Електричний струм

За означенням, сила струму є похідною від кількості електрики q= q(t),

де t-час, тобто I(t)= q(t).

Задача 1 (про значення змінного струму, який проходить по провіднику)

Через поперечний переріз провідника проходить заряд, який обчислюється за формулою q =. Знайти силу струму в момент часу 4с.

Математичний метод

Дано: Розв’язок:

q = Відомо, що сила струму є похідною від заряду, отже

Знайти: I = q(t) = = ;

І - ? через 4с I = = А.

Відповідь: А

Функція q=q(t) є первісною для функції І=I(t), тому кількість електрики, що проходить через поперечний переріз провідника за час від t₁до t₂, можна знайти за формулою

Задача 2. Знайти кількість електрики, що проходить через поперечний переріз провідника за 10с, якщо сила струму змінюється за законом I (t) = (4t + 1) A.

Математичний метод

Дано: Розв’язок:

I (t) = (4t + 1) А . Відомо, q=q(t) є первісною для функції І=I(t), отже

t =10с

Знайти:

- ? Відповідь: .

3.2. Електромагнітні коливання

Змінні електричні і магнітні поля не можуть існувати одне від одного, оскільки в просторі, де існує змінне магнітне поле, збуджується електричне поле і навпаки. Одночасні періодичні зміни пов’язаних між собою електричного і магнітного полів утворюють електромагнітні коливання.

Виведемо рівняння, яке описує процеси у коливальному контурі.

ᴖᴖᴖ Повна електромагнітна енергія W контура в будь-який

момент часу дорівнює сумі енергій магнітного і

електричного полів: .

Ця енергія не змінюється з часом, якщо опір контура R дорівнює 0. Тому похідна дорівнює нулю.

або .

Фізичний зміст цього рівняння: швидкість зміни магнітного поля по модулю дорівнює швидкості зміни енергії електричного поля. Мінус означає наступне: коли магнітне поле зменшується, електричне поле збільшується і навпаки.

Обчислимо похідні:

, але q= i, тож отримуємо Lii = .

і=q, отже Lq = - , .

Незатухаючі коливання називаються вимушеними електричними коливаннями. Прикладом вимушених коливань є змінний струм.

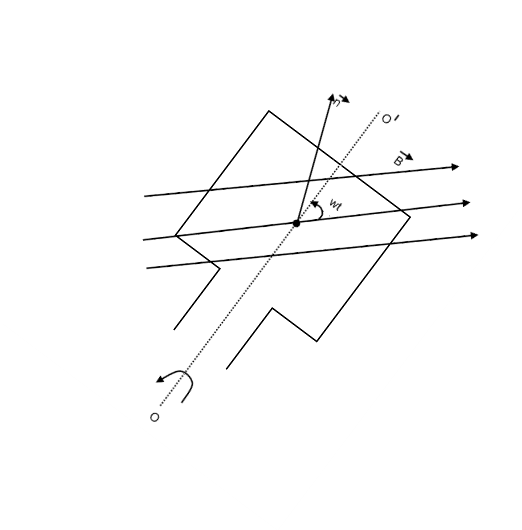Розглянемо плоский прямокутний контур (рамка), який обертається навколо осі 00’

Магнітний потік , який пронизує контур у будь-який момент часу:

де В – індукція магнітного поля,

S – площа, обмежена контуром,

– циклічна частота.

Під час обертання рамки виникає змінна ЕРС індукції:

Оскільки то

Розв’яжемо задачу 3. Запишіть, закон зміни ЕРС, що індукується в рамці площею 100 см², що обертається із частотою 50 Гц у магнітному полі з індукцією 0,2 Тл, якщо в початковий момент площина рамки перпендикулярна до ліній індукції магнітного поля.

Дано: Розв’язок

S = 100 см²0,01 м²Згідно формули

ν = 50 Гц . В=0,2 Тл

= (t) -? Отже отримуємо закон зміни ЕРС, яка

індукується в рамці:

Відповідь:

Постійний струм не може існувати в колі, який містить конденсатор, тому що коло фактично розімкнуте. Розглянемо коло, яке містить конденсатор та джерело змінного струму.

Знайдемо як змінюється сила струму в колі.

С Напруга на конденсатор обчислюється за

формулою , отже .

Заряд конденсатора змінюється по гармонічному закону:

Так, як сила струму обчислюється як похідна заряду по часу, то

Отже,

Індуктивність в колі впливає на силу змінного струму. Сила струму змінюється за законом .

ᴖᴖᴖ Робота вихревого поля по переміщенню одиничного

додатного заряда дорівнює за модулем

і протипожежна за знаком роботі

кулонівського поля:

ЕРС самоіндукції обчислюється: ,

отже , де - амплітуда коливаня напруги.

Розв’яжемо задачу 4: Котушка з індуктивністю 0,008 Гн приєднана до джерела змінної напруги із частотою 1000 Гц. Діюче значення напруги 100 В. Визначити амплітуду струму в колі.

Дано: Розв’язок

L = 0,08Гн Згідно формули ,

ν = 1000Гц отже

U = 100 В Діюче значення напруги обчислюється за формулою

Imax - ? , отже

Циклічна частота отже, отримуємо формулу

Підставимо значення величин у формулу:

Відповідь: 0,28 А.

Розв’яжемо задачу 5. Заряд на пластинах конденсатора коливального контура змінюється з часом t за законом . Записати закон залежності сили струму від часу . Визначити період і частоту коливань у контурі, амплітуду коливань заряду і амплітуду коливань сили струму.

Дано: Розв’язок:

Заряд на пластинах конденсатора змінюється за

законом: ,

T - ? отже ,.

ν - ? Циклічна частота обчислюється за формулою:

звідси .

Період коливань: , .

Сила струму обчислюється, як похідна заряду з часом:

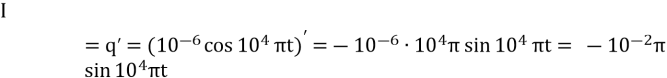
Отже .

Відповідь: .

РОЗДІЛ 4

ЯДЕРНА ФІЗИКА

Кожний радіоактивний елемент має період піврозпаду, час через який майже половина атомів розпадається. Виведемо закон радіоактивного розпаду.

Число атомів dN, які розпадаються за час dt, пропорційно часу і числу N атомів радіоактивного елемента

, де- постійна розпаду даного елементу.

Інтегруємо дане рівняння, отримуємо

, отже

Розв’яжемо задачу 1: Період піврозпаду дорівнює 30 років. За який інтервал часу на забрудненій після Чорнобильської катастрофи території, кількість ядер зменшиться в 4 рази.

Дано: Розв’язок:

Т = 30 р ;

;; ;

t - ?

Відповідь: 60 років.

ВИСНОВКИ

В своїй роботі я розглянув різні фізичні процеси: механічні, електромагнітні, ядерні.. І впевнився, що вивчення фізичних явищ пов’язано з виведенням складних формул, законів із використанням знаходження похідної функції та інтегрування. Тобто вивчення фізики використовує апарат математичного аналізу.

Зв’язок фізики і математики очевидний. Математика є фундаментом, на якому будуються всі фізичні закони і формули. Вона збагачує фізику своїми досягненнями, при чому розвивається і удосконалюється сама. Інформаційні технології дають змогу прискорити процес отримання результату, шляхом застосування програми Microsoft Excel

Будь-яка сучасна людина, незалежно від її професійної діяльності, повинна знати основи фізики, інформаційних технологій і математики і вміти творчо застосовувати набуті знання і вміння на практиці.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ ІНФОРМАЦІЇ

1.Кушнір Р.М. Загальна фізика. Механіка. Молекулярна фізика.- Львів: Вид. центр ЛНУ, 2003.-176с

2.Бушок Г.Ф. Курс фізики: У двох книгах: Навчальний підручник для студентів фізико-мат. спец. вищих педагогічних навчальних закладів освіти. Кн.2. Оптика. Фізика атома і атомного ядра. Молекулярна фізика і термодинаміка/ Г.Ф.Бушок, Є.Ф.Венгер.- К.: Либідь, 2001.- 424с.

3.Загальна фізика. Механіка.- К.: НАУ, 2003.- 40с.

4.Фізика 7-11 класи.- К.: Шкільний світ, 2001.- 95с.

5.Гончаренко С.У. Фізика.- К: Освіта, 2002.- 319с.

6.Коршак Є.В. та ін. Фізика. 7 кл..- К., Ірпінь: Перун, 2003.- 160с.

7.Коршак Є.В. та ін. Фізика. 8 кл..- К., Ірпінь: Перун, 2003.- 192с. ..

8.Грабовський Р.І. Курс фізики для аграрного інститута . Навчальний посібник 5-видання- М., Вища школа,2000. -607с

9.Кошкін М.І.Елементарна фізика-Наука.Фізмат, 2001.-236с