Старовинні геометричні задачі
Про матеріал
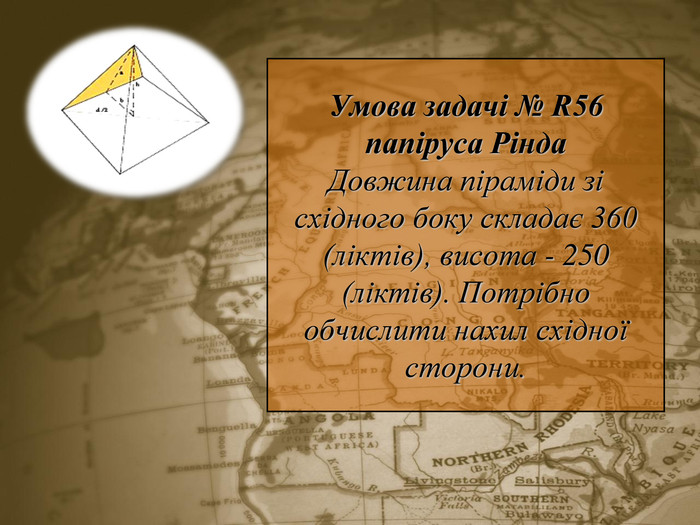
Практична робота. Розв'язування стародавніх геометричних задач містить задачі папіруса Ахмеса (Рінда). В них показані способи обчислення нахилу піраміди вліво, вправо, практичні задачі побутового змісту. Розв'язування даних задач сприяє розвитку логічного мислення учнів 10-11 класів з теми «Піраміда», відпрацювання навичок виконання практичних робіт, проектів.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку

























-

Данко Наталія Вікторівна
31.03.2018 в 21:54
+++
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Пихтіна Лілія
31.03.2018 в 16:30
Добре
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лучинський Михайло
31.03.2018 в 15:19
+++
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Глоба Марина Анатоліївна
31.03.2018 в 07:24
)))
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Бойкова Тетяна Іванівна
30.03.2018 в 22:13
+++++
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ревенко Елена
30.03.2018 в 20:48
Чудово
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Радченко Зоя
30.03.2018 в 18:52
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Радченко Зоя
30.03.2018 в 18:52
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Пономаренко Ольга
30.03.2018 в 17:54
+++
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сташук Валентина
30.03.2018 в 15:24
)))
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Жаннусик Жанна
30.03.2018 в 14:06
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гладких Галина
30.03.2018 в 12:21
)))
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Zhadan Nastya
30.03.2018 в 12:16
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Shumelchuk Katerina
30.03.2018 в 09:17
+++
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гриценко Костя
30.03.2018 в 09:06
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Казак Валеріан
29.03.2018 в 22:28
Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Khonor Lady
29.03.2018 в 21:42
Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Осокіна Кіра
29.03.2018 в 16:26
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Shumelchuk Alla
29.03.2018 в 13:28
+++
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тупало Ольга
29.03.2018 в 12:22
)))+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Васильєва Ірина Григорівна
29.03.2018 в 10:27
класс
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Плугарь Максим
28.03.2018 в 23:11
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Яким Давид Петрович
28.03.2018 в 22:42
+++
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Князьков Олександр Сергійович
28.03.2018 в 21:41
+++
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Tarasov Anton
28.03.2018 в 20:46
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Фурсова Анна
28.03.2018 в 14:55
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Морозова Галина
28.03.2018 в 13:23
Дуже цікаво!!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Казак Ольга Іванівна
28.03.2018 в 11:34
+++
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мунтяну Виолетта
24.03.2018 в 23:26
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Недильска Валерия
24.03.2018 в 16:51
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Lazareva Julia
23.03.2018 в 20:23
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шведова Катерина
23.03.2018 в 19:32
добре
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Прудченко Иван
23.03.2018 в 13:24
*
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Прудченко Иван
23.03.2018 в 13:24
*
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Прудченко Иван
23.03.2018 в 13:23
*
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тітова Анастасія Олександрівна
23.03.2018 в 09:07
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кузьменко Наталья
22.03.2018 в 22:37
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Жук Антон
22.03.2018 в 19:42
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тонкопрядко Анна
22.03.2018 в 19:36
++++
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Дранова Александра
22.03.2018 в 14:01
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гужеля Олександра Миколаївна
22.03.2018 в 12:58
)))))))
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Konina Katerina
22.03.2018 в 12:45
)
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Абрамян Артём
22.03.2018 в 12:18
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Паша Титаренко
22.03.2018 в 10:05
)))
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Осокина Валерия
22.03.2018 в 09:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kazak Dashulya
21.03.2018 в 22:35
)))
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шевченко Наталя Володимирівна
21.03.2018 в 21:47
+
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Галета Дарья
21.03.2018 в 20:58
Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шелудько Ніна Степанівна
21.03.2018 в 20:57
Добре!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Фурсова Ірина
21.03.2018 в 19:56
Чудово
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Качуровська Ірина Іванівна
21.03.2018 в 19:36
Дуже добре)
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Караба Яна Сергїївна
21.03.2018 в 17:07
)
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Чекалова Оксана Едуардівна
21.03.2018 в 15:21
Чудово)
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шумельчук Ирина
21.03.2018 в 14:14
++++
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вінницька Олена
21.03.2018 в 13:05
Клас
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 52 відгука