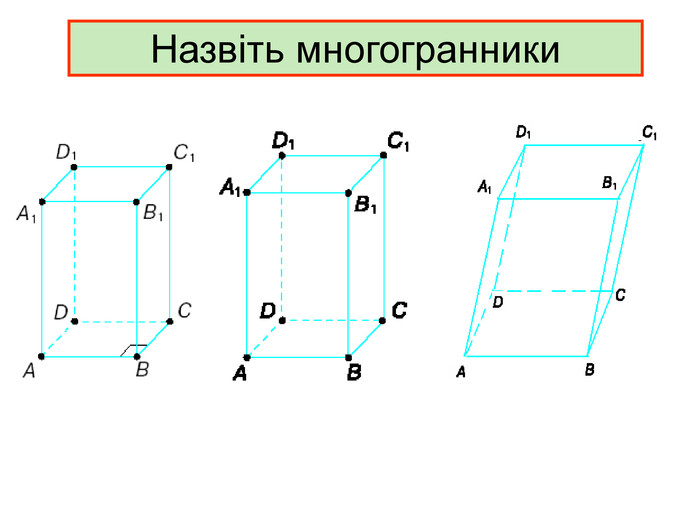
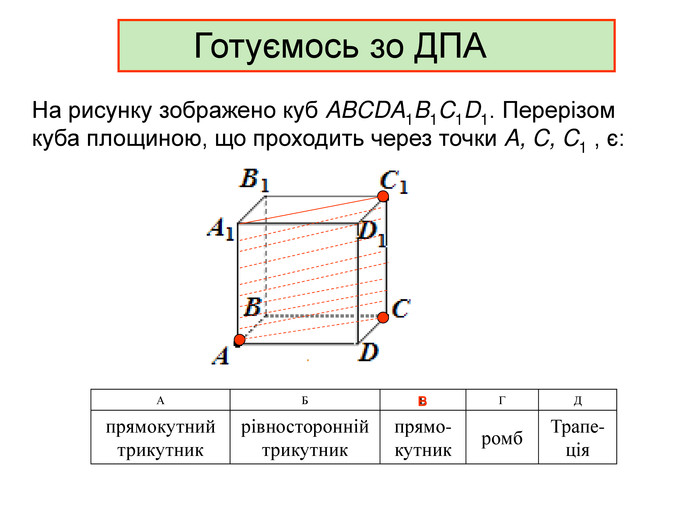
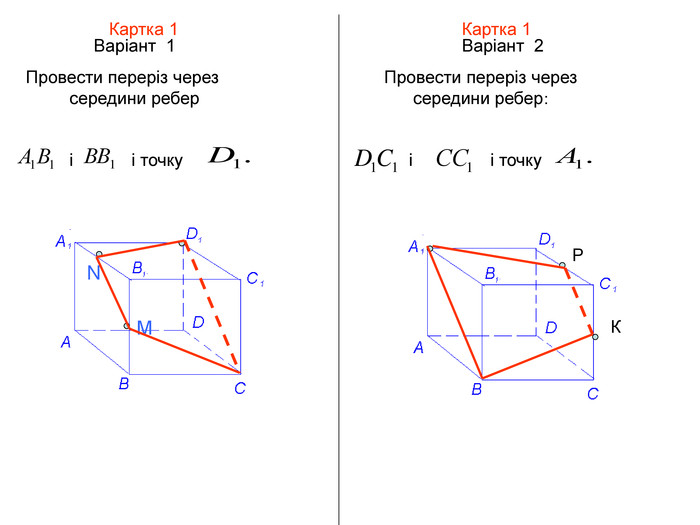
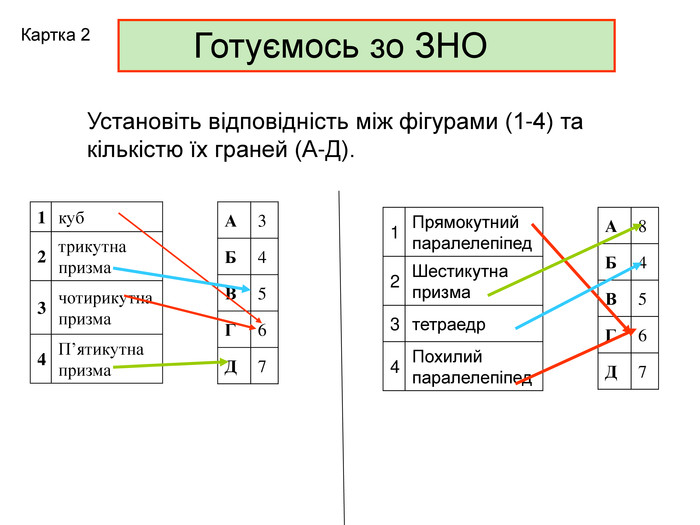
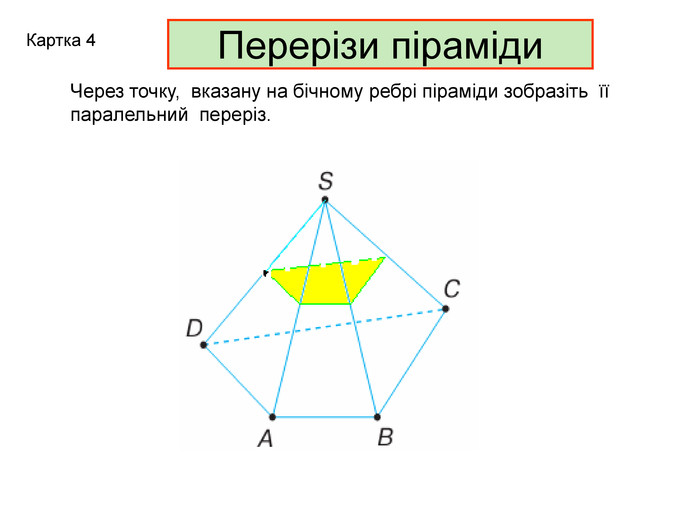
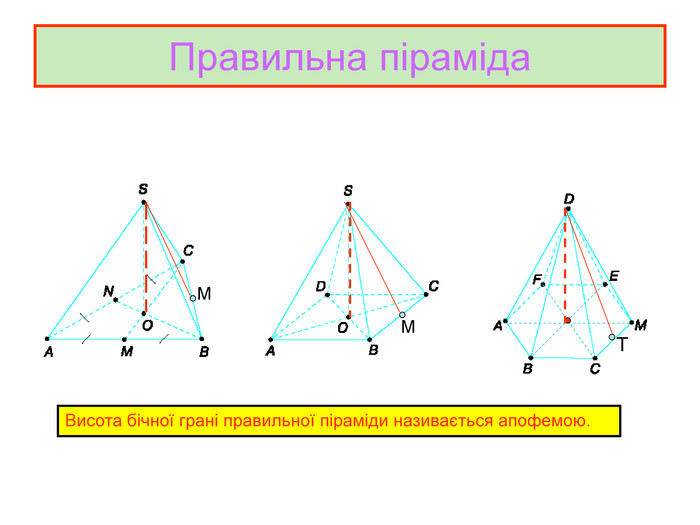
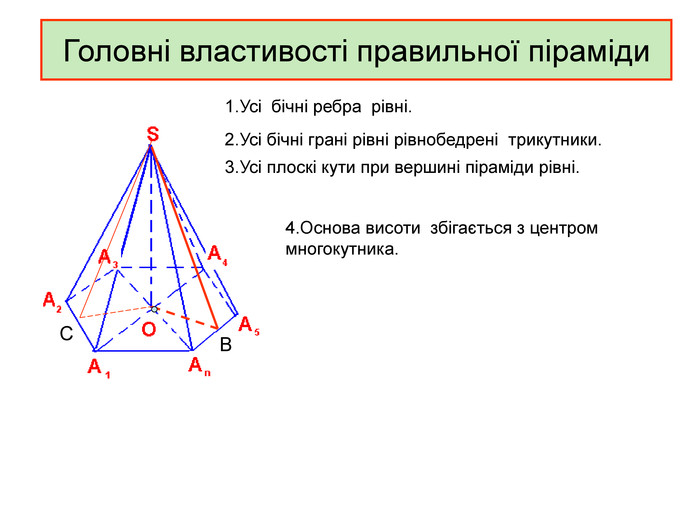
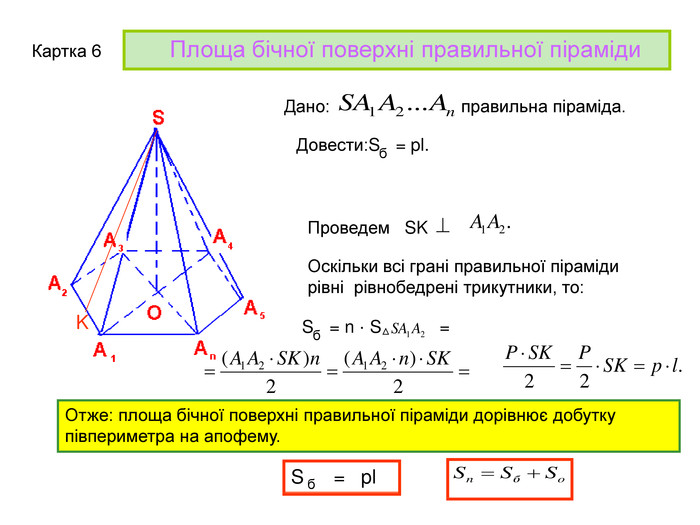
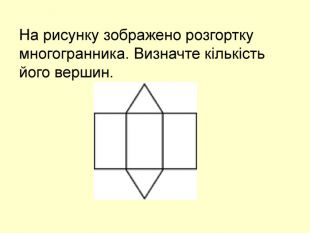
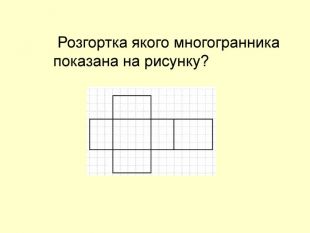
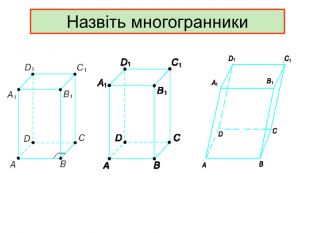
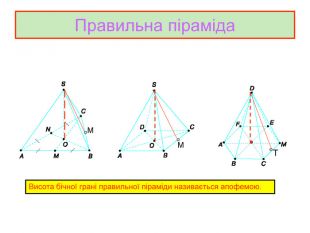
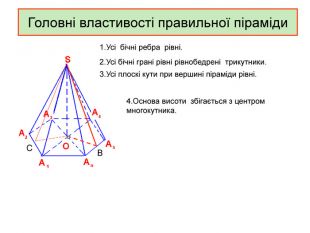
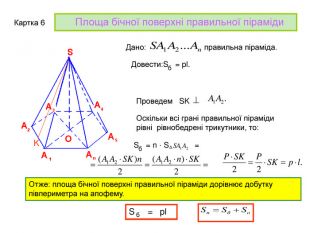
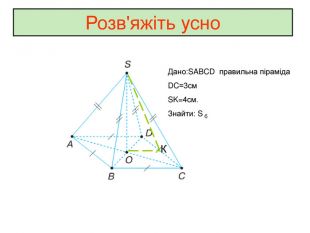
Презентація до уроку з геометрії в 11 класі "Піраміда.Бічна та повна поверхня правильної піраміди"
Про матеріал
Презентація до уроку з геомет
____________________________________________________________________
______________________________________________________________________
______________________________________________________________________
Перегляд файлу
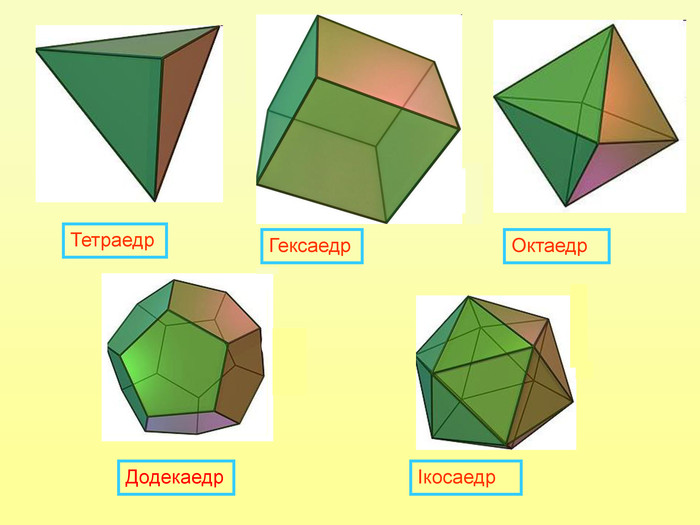
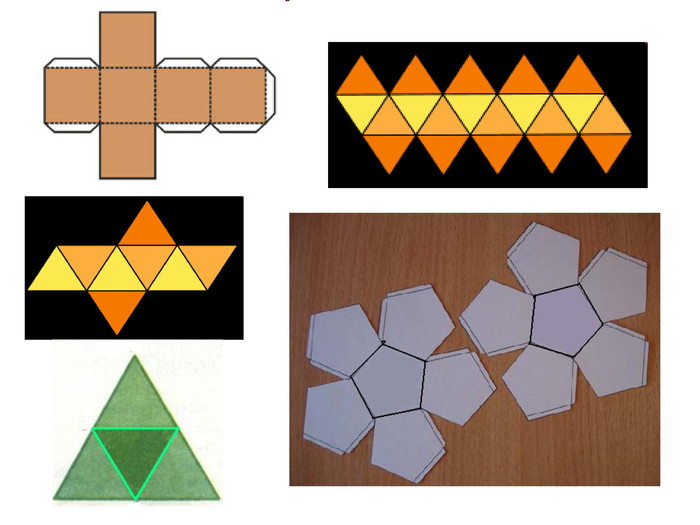
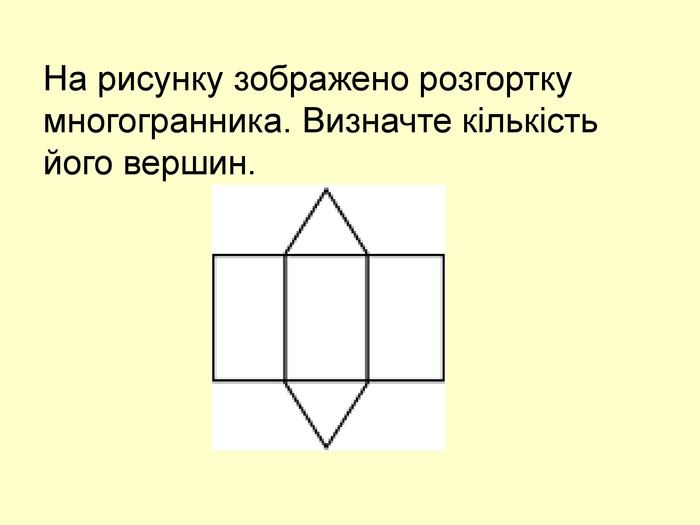
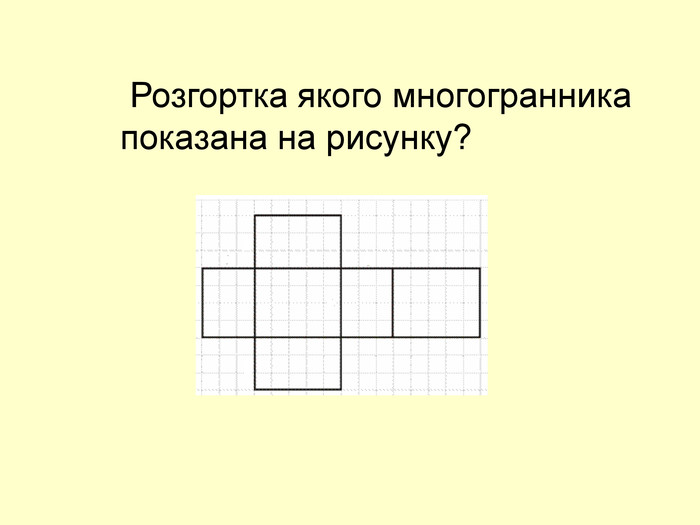
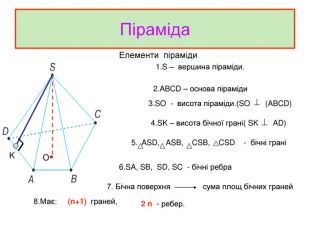
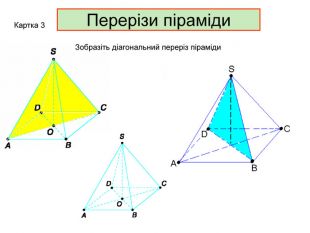
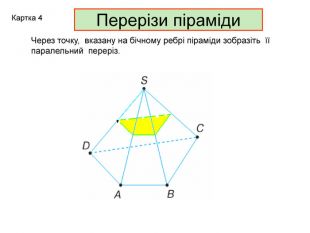
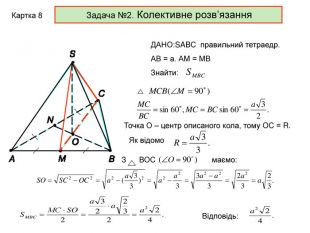
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Геометрія (академічний, профільний рівень) 11 клас (Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку