Стаття "Деякі питання щодо вивчення квадратних рівнянь у школі

Вивчення квадратних рівнянь у 8 класі

Теорія рівнянь в шкільному курсі займає провідне місце. Це пов’язано з тим, що більшість задач прикладного змісту зводяться до розв’язування різних видів рівнянь. Серед них провідне місце належить квадратним рівнянням, оскільки розв’язок більшості рівнянь тим чи іншим чином зводиться до квадратних.

В практичній діяльності часто зустрічаються рівняння в тому числі і квадратні або такі, розв’язання яких зводиться до квадратних, розв’язок яких потребує довгих обчислень, які є громіздкими і не завжди приводять до бажаного результату. І, як наслідок, виникає питання: чи існують більш прості, раціональні та елегантні способи їх розв’язання.

У 8-му класі здобувачі освіти знайомляться з декількома видами квадратних рівнянь і відпрацьовують їх розв’язок за відомими формулами. Проте програма шкільного курсу математики на рівні стандарту не передбачає ознайомлення здобувачів освіти з іншими прийомами, які для великої кількості рівнянь є більш раціональними та простими. Серед таких прийомів – застосування властивостей коефіцієнтів повного квадратного рівняння, застосування теореми Вієта, наслідків з теореми Безу, розкладання лівої частини рівняння на множник тощо. 

Застосування цих прийомів до досить непростих квадратних рівнянь та рівнянь, розв’язання яких пов’язане з квадратними, необхідно показувати учням. Вони мають самі в подальшому добирати зручні способи, що забезпечить формування прийомів аналізу, узагальнення, алгоритмізації. Поряд з формулами для знаходження коренів квадратного рівняння необхідно давати і формули, які застосовують при певній залежності між коефіцієнтами повного квадратного рівняння, щоб учні їх добре запам’ятали та користувалися в подальшому.

І.  Використання властивостей коефіцієнтів повного квадратного рівняння

Для рівняння         𝒂𝒙^𝟐 + 𝒃𝒙 + 𝒄 = 𝟎, 𝒂 ≠ 𝟎                     (1)

ü Якщо 𝒂 + 𝒃 + 𝒄 = 𝟎, то 𝒙_𝟏 = 𝟏, 𝒙_𝟐 = 𝒄: 𝒂

ü Якщо 𝒂 − 𝒃 + 𝒄 = 𝟎, то 𝒙_𝟏 = −𝟏, 𝒙_𝟐 = −𝒄: 𝒂

ü Якщо 𝒃 = 𝒂^𝟐 + 𝟏, 𝒂 = 𝒄, то  𝒙_𝟏 = −𝒂, 𝒙_𝟐 = −𝟏: 𝒂

ü Якщо 𝒃 = 𝒂^𝟐 − 𝟏, 𝒂 = −𝒄  то  𝒙_𝟏 = −𝒂, 𝒙_𝟐 = 𝟏: 𝒂

ü Якщо 𝒃 = −(𝒂^𝟐 + 𝟏),𝒂 = 𝒄, то 𝒙_𝟏 = 𝒂, 𝒙_𝟐 = 𝟏: 𝒂

ü Якщо 𝒃 = −(𝒂^𝟐 − 𝟏),𝒂 = −𝒄, то 𝒙_𝟏 = 𝒂, 𝒙_𝟐 =

−𝟏: 𝒂

           Наведемо приклади розв’язання рівнянь.

           Розв’язати рівняння

1.  4271𝑥² − 4272𝑥 + 1 = 0

           Розв’язання

Оскільки

𝑎 + 𝑏 + 𝑐 = 4271 − 4272 + 1 = 0, 

𝑐                1  то                   𝑥₁ = 1, 𝑥₂ ⁼ _𝑎 ⁼ ₄₂₇₁ 

Відповідь:      ,    1.

 𝟐.  939𝑥² + 978𝑥 + 39 = 0

          Розв’язання

Для заданого рівняння

𝑎 − 𝑏 + 𝑐 = 939 − 978 + 39 = 0, 

   Тоді                𝑥₁ = −1, 𝑥₂ = − _𝑎^𝑐 = − .

Відповідь:  −  , −1.

 𝟑.  41𝑥² + 1682𝑥 + 41 = 0

          Розв’язання

В цьому випадку

𝑏 = 𝑎² + 1 = 41² + 1 = 1681 + 1 = 1682, 𝑎 = 𝑐 = 41, 

 тому

                                                                                                                            1            1

𝑥₁ = −𝑎 = −41, 𝑥₂ = −  = −  

                                                                                                                            𝑎          41

Відповідь:   −41, − .

 𝟒.  26𝑥² + 675𝑥 − 26 = 0

         Розв’язання

Так як

𝑏 = 𝑎² − 1 = 26² − 1 = 676 − 1 = 675,𝑎 = 26 = −(−26) = −𝑐,  

тоді        𝑥₁ = −𝑎 = −26, 𝑥₂ = _𝑎¹ = ₂₆¹

Відповідь:  −26, .

 𝟓.  41𝑥² − 1682𝑥 + 41 = 0

        Розв’язання

Для цього рівняння

                                                𝑏 = −(𝑎² + 1) = −(41² + 1) = −1642,            𝑎 = 𝑐 = 41,

 Тому             𝑥₁ = 𝑎 = 41, 𝑥₂ ⁼ _𝑎^{1 =} ₄₁¹ .

Відповідь:    , 41.  𝟔.  − 84𝑥² − 7055𝑥 + 84 = 0

       Розв’язання

Маємо

𝑏 = −(𝑎² − 1) = −((−84)² − 1) = −(7056 − 1) = −7055

𝑎 = −𝑐 = −84,

1               1 тому                𝑥₁ = 𝑎 = −84, 𝑥₂ = − _𝑎 = ₈₄.

Відповідь:  −84, .

Вправи для самостійної роботи.

1.     5432𝑥² − 3087𝑥 − 2345 = 0

2.     55𝑥² − 44𝑥 − 11 = 0

3.     1999𝑥² + 2000𝑥 + 1 = 0

4.     313𝑥² + 326𝑥 + 13 = 0

5.     25𝑥² + 626𝑥 + 25 = 0

6.     5𝑥² + 26𝑥 + 5 = 0

7.     2021𝑥² + 4084440𝑥 − 2021 = 0

8.     7𝑥² + 48𝑥 − 7 = 0

9.     13𝑥² − 170𝑥 + 13 = 0

10.48𝑥² − 2303𝑥 − 48 = 0

ІІ. Використання теореми Вієта

       Теорема Вієта відіграє велику роль у розв’язуванні квадратних рівнянь, оскільки будь-яке повне квадратне рівняння можна привести до зведеного, яке в окремих випадках можна розв’язати усно. Здобувачам освіти варто показати приклади застосування теореми до рівнянь, до яких, на перший погляд, її застосувати неможливо.

           Розв’язати рівняння.

1. 𝑥² + 3𝑥 − 28 = 0 За теоремою Вієта

{𝑥₁ ∙ 𝑥₂ = −28,  ⟺ ⟦𝑥₁ = −7, 

                                   𝑥₁ + 𝑥₂ = −3;                𝑥₂ = 4.

Відповідь:       4;   -7.

𝟐. 2𝑥² + 9𝑥 − 5 = 0.                                                     (2)

Дане повне рівняння можна звести до зведеного розділивши на 2, отримаємо рівняння 

𝑥² + 4,5𝑥 − 2,5 = 0.   Це рівняння має дробові корені, тому безпосередньо розв’язувати такі рівняння за теоремою Вієта складно. Зведемо його до рівняння, яке легко розв’язати усно, помноживши рівняння (2) на 2. Отримаємо 

             4𝑥² + 18𝑥 − 10 = 0.

              Нехай 𝑦 = 2𝑥, тоді маємо

² + 9𝑦 − 10 = 0. ⟺ ⟦𝑦 = −10,

               𝑦

𝑦 = 1.

               𝑥₁ =  = −5, 𝑥₂ = ¹₂ = 0,5.

 Відповідь: -5; 0,5.

 𝟑.  3𝑥² − 8𝑥 + 4 = 0. Розв’язання

Помножимо дане рівняння на 3, одержуємо

(3𝑥)² − 8 ∙ 3𝑥 + 12 = 0.

Заміна: 𝑦 = 3𝑥.

² − 8𝑦 + 12 = 0 ⟺ ⟦𝑦 = 6, 

𝑦

𝑦 = 2.

𝑦¹𝑦²

𝑥₁ = ₃ == 2,       𝑥₂ = ₃ =. 

Відповідь:      2,   .

Вправи для самостійної роботи.

1.     3𝑥² + 5𝑥 − 8 = 0.

2.     3𝑥² − 𝑥 − 4 = 0.

3.     5𝑥² − 3𝑥 − 8 = 0.

4.     4𝑥² + 3𝑥 − 7 = 0.

             ІІІ. Метод перекидання

        Під час розв’язання попереднього квадратного рівняння має сенс здобувачів освіти познайомити зі способом «перекидання» першого коефіцієнта з метою одержання зведеного квадратного рівняння, яке легко розв’язується шляхом усного добору коренів.

       Повне квадратне рівняння, яке має дробові корені, легко розв’язувати усно за теоремою Вієта, застосувавши до нього метод перекидання. Нехай задано повне квадратне рівняння

𝑎𝑥² + 𝑏𝑥 + 𝑐 = 0,                                                                              (1)   

що має раціональні корені 𝑥₁ та  𝑥₂.  Помножимо обидві частини рівняння на 𝑎, дістанемо:

𝑎²𝑥² + 𝑏𝑎𝑥 + 𝑎𝑐 = 0.

Позначимо 𝑎𝑥 = 𝑦.  Рівняння набере вигляду

𝑦² + 𝑏𝑦 + 𝑎𝑐 = 0.                                                                                          (3)

Рівняння (3) відрізняється від рівняння (1) тим, що перший коефіцієнт дорівнює 1, а останній-добутку крайніх коефіцієнтів. Рівняння (3) стало зведеним і таким, що має цілі корені. Отже, їх легко знайти усно, використовуючи теорему Вієта. Нехай це будуть 𝑦₁ та 𝑦₂. Тоді 𝑎𝑥₁ = 𝑦₁,

𝑎𝑥₂ = 𝑦₂. Звідки

                                                                                          𝑦1                             𝑦2

                                                                             𝑥₁ =  ,           𝑥₂ = .

                                                                                           𝑎                        𝑎

Алгоритм використання методу перекидання

Щоб повне квадратне рівняння, яке має дробові корені, розв’язати усно треба:

1.     Звести дане рівняння   

𝑎𝑥² + 𝑏𝑥 + 𝑐 = 0

до рівняння виду

𝑦² + 𝑏𝑦 + 𝑐 = 0.

2.     Кожний       корінь,        одержаний після розв’язання          зведеного квадратного рівняння, поділити на перший коефіцієнт повного квадратного рівняння.

Наприклад 

           Розв’язати рівняння

1. 4𝑥² + 9𝑥 + 2 = 0 Розв’язання

Перекинемо перший коефіцієнт до вільного члена, помноживши його на

4, одержуємо нове рівняння, що розв’язується усно за теоремою Вієта 𝑦² + 9𝑦 + 8 = 0. 

 𝑦₁ = −1, 𝑦₂ = −8. 

Тому    𝑥₁ = ^𝑦₄¹ =  = − ¹₄ , 𝑥₂ = ^𝑦₄² =  = −2.

Відповідь:    −2, − .

 𝟐.  28𝑥² + 77𝑥 + 49 = 0.

          Розв’язання

         Поділимо кожен член заданого  рівняння на 7, одержимо  рівняння                      4𝑥² + 11𝑥 + 7 = 0. 

Здійснимо перекидання першого коефіцієнта до вільного члена, отримаємо рівняння

y² + 11y + 28 = 0;  𝑦₁ = −4, 𝑦₂ = −7. 

𝑦¹𝑦²

Отже,           𝑥₁ = ₄ == −1,     𝑥₂ = ₄ == −.

Відповідь:   −  , −1.

Вправи для самостійної роботи.

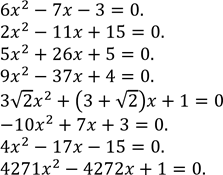1.

2.

3.

4.

5..

6.

7.

8.

         ІV.  Метод Султанова

        Для здобувачів освіти не зайвим буде і метод Султанова, оскільки він дозволяє розвивати уяву, обчислювальні навички, формування навичок підстановки, які необхідні при розв’язанні переважної більшості вправ ДПА та ЗНО.

Його зміст полягає в наступному. Задане повне квадратне рівняння (1) ділять на змінну 𝑥, оскільки число 0 не являється коренем рівняння (1). Одержане рівняння записують так:

                                       𝑎𝑥 + 𝑏 = ^𝑐                                                   (4)

𝑥

для зручності усного знаходження цілого числа,  що є дільником вільного члена рівняння (1), яке задовольняє обидві частини рівняння (4). Знайдене число буде першим коренем рівняння (1). Другий корінь знаходять за формулою

𝑥₂ = 𝑐: 𝑎: 𝑥₁

           Наведемо приклади розв’язання повних квадратних рівнянь із застосуванням методу Султанова.

          Розв’язати рівняння.

1.  5𝑥² + 26𝑥 + 5 = 0                                            (5)

Розв’язання

 Поділимо рівняння (5) на 𝑥 (𝑥 ≠ 0) та перевіримо кожний з дільників вільного члена рівняння (5) чи не є він коренем.

                                                              (6)

𝑥   

Підставляючи значення дільників у рівняння (6), швидко з’ясовуємо, що число -5 є коренем рівняння (5), тобто 𝑥₁ = −5.   Другий корінь знаходимо за формулою

                 𝑥₂ = 𝑐: 𝑎: 𝑥_1.               𝑥₂ = 5: 5: (−5) = −0,2.

Відповідь:     -0,2; -5.

𝟐.   354𝑥² − 52𝑥 − 302 = 0.                           (7)

Розв’язання

Записуємо рівняння (7) у вигляді

302

354𝑥 − 52 = .                  (8)              

𝑥

Швидко знаходимо перший корінь рівняння (8), підставивши число 1, тобто                     𝑥₁ = 1.

 Другий корінь 𝑥₂ = 𝑐: 𝑎: 𝑥₁,   𝑥₂ = −302: 354: 1 = − .

Відповідь: 1; − .

 𝟑.  2017𝑥² + 𝑥 − 2016 = 0.                            (9)

Записуємо рівняння (9) у вигляді

2016

2017𝑥 + 1 = .

𝑥

 Дільник вільного члена, число -1, є коренем рівняння (9), тобто           𝑥₁ = −1.

 Другий корінь рівняння (9) 𝑥₂ = 𝑐: 𝑎: 𝑥₁.     

𝑥₂ = −2016: 2017: (−1) = − .

Відповідь: -1; − .

𝟒. 20𝑥² − 9𝑥 + 1 = 0.                                              (10)

         Жоден з дільників вільного члена не є коренем рівняння (10), тому дане рівняння цілих коренів немає. Скористаємося методом перекидання.

Записуємо рівняння у вигляді

𝑦² − 9𝑦 + 20 = 0.                                                 (11)

Поділимо рівняння (11) на 𝑦, 𝑦 ≠ 0, отримаємо

20

𝑦 − 9 = − .

𝑦

  Дільник вільного члена рівняння (11), число 4, є коренем рівняння (11), тобто 𝑦₁ = 4. 

Тоді другий корінь рівняння (11)

𝑦₂ = 𝑐: 𝑎: 𝑦₁ = 20: 1: 4 = 5.

  Корені рівняння (10) дорівнюють  

                                                                                𝑦₁         1                      𝑦₂         1

                                                                   𝑥₁ =        =     ,          𝑥₂ =        =   

                                                                                20      5                      20      4

Відповідь: 0,2;  0,25.

Вправи для самостійної роботи.

1. 319𝑥²1988𝑥 + 1669 = 0 2. 1978𝑥² − 1984𝑥 + 6 = 0.

3.     2𝑥² − 9𝑥 + 9 = 0.

4.     5𝑥² − 11𝑥 + 2 = 0.

5.     2𝑥² + 13𝑥 + 15 = 0.

Висновок

        Тема «Квадратні рівняння» в повній мірі забезпечує компетентнісний підхід до викладання математики. Ця тема дає можливість формувати у здобувачів освіти такі математичні компетентності як аналіз, самостійність вибору, раціоналізм, вдумливий підхід до вирішення життєво важливої проблеми.

Працюючи з восьмикласниками, є сенс дати їм певні рекомендації при розв’язанні квадратних рівнянь.

1.                 Здійснити перевірку чисел 1 та -1 на належність їх до коренів заданого квадратного рівняння. Якщо одне з чисел є коренем, то для знаходження другого кореня доцільно застосовувати залежність між коефіцієнтами квадратного рівняння, метод Султанова.

2.                 При наявності повного квадратного рівняння доречно звести його до зведеного і знайти корені за теоремою Вієта. Якщо ж це зробити важко – застосувати метод перекидання. 

3.                 Якщо задане повне квадратне рівняння має цілий корінь, який легко знайти методом добору, то для знаходження другого кореня застосувати метод Султанова.

4.                 Для перевірки наявності цілих коренів їх шукають серед дільників вільного члена. Причому з дільників вільного члена, відмінних від чисел 1  та  -1, потребують випробування лише ті, для кожного з яких

𝑓(1)               𝑓(−1) обидві частки           ,             є цілі числа, де 𝑎 – дільник вільного члена.

                                          1−𝑎         1+𝑎