Урок на тему: " Застосування показникової та логарифмічної функцій у реальних процесах"

Міністерство освіти і науки України

Одеський коледж транспортних технологій

 

 

 

 

ОПИС

ВІДКРИТОГО ЗАНЯТТЯ

 

Навчальна дисципліна          Математика

 

 Тема: «Застосування показникової та логарифмічної функції до опису реальних процесів.»

 

Розробив викладач Милова М. А.

                                                                     « 11 » квітня 2019 р.

 

Погоджено

Голова  циклової комісії       / Іванова Г.С. /

«_03__»_квітня_   2019 р.

 

2018-2019 н. р.

 

 

ПРОТОКОЛ  ВІДКРИТОГО ЗАНЯТТЯ

 

Дата відвідання: 11.04.2019р.

 

Мета відвідання:  Вивчення досвіду роботи викладача.  Вивчення методики проведення  семенарсько- практичного заняття.

 

Прізвище, ім’я, по батькові викладача, заняття якого відвідане

 

МИЛОВА МАРИНА АНАТОЛІЇВНА

Відвідувачі: Бердичевська Т. М., Зелінська С.В., Іванова Г. С., Ільїна Н. О.

Товстік Ж.В., Шумська Л. О., Жебова Р. В.,Покась М. В.

Група ТЕ-11

Кількість студентів на занятті  29

Кількість студентів за журналом  30

Предмет : Математика

Тема:  « Застосування показникової та логарифмічної функцій до опису реальних процесів»

 Вид заняття  Семенарсько-практичне заняття

 

 

 

 

 

 

Забезпечення заняття

 

Наочність	Роздатковий матеріал
Презентація «Властивості функцій» «Застосування логарифмічної  та показникової  функцій»	Опорні конспекти, тестові завдання,  карта оцінювання студента.

 

         

 

 

 

 

 

 

Дата: 11.04.2018 р.

Група:  ТЕ-11

Викладач: Милова М.А.

 

 

 

 

 

 

 

 

 

 

 

Міністерство освіти і науки України

Одеський коледж транспортних технологій

 

 

 

Методична розробка

заняття з математики

 

 

 

 

2019 р.

Компетентності:

Знаннєвий компонент (предметні компетентності)

Студент:

 - розуміє  суть поняття «функція», «показникова та логарифмічна функція»;

 - називає  властивості та види функцій;

 - знає формули показникової та логарифмічної функцій;

 - усвідомлює застосування  показникової та логарифмічної функцій у реальних процесах;

 - застосовує вивчені властивості показникової  та логарифмічної функцій для розв’язування конкретних завдань.

Діяльнісний компонент (ключові компетентності)

Студент:

• володіє ефективними прийомами пошуку необхідної інформації з даної теми;
• володіє формулами з даної теми;
• виділяє необхідну інформацію щодо даної теми;
• використовує знайдену інформацію на заняттях.

Ціннісний компонент (емоційно-ціннісне ставлення)

Студент:

- показує пізнавальний інтерес до математики;

- демонструє активність, ініціативність на занятті;

- демонструє наполегливість у досягненні мети, уміння працювати у колективі, взаємодопомогу, культуру спілкування.

 

Тривалість : 80 хвилин

Тип заняття: семінарсько-практичне.

Обладнання:

1. Набір слайдів для повторення і вивчення нового матеріалу.
2. Мультимедійный проектор.
3. Індивідуальні карточки-завдання.

 

 

 

 

 

 

Література:

1. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенко А.К. Математика (підручник для студентів ВНЗ І-ІІ р.а. технічних спеціальностей) – К.: Вища школа, 2001
2. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенко А.К. Дидактичні матеріали з математики (навчальний посібник для студентів ВНЗ І-ІІ р.а.)       – К.: Вища школа, 2001
3. Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу (підручник) , 10-11 кл. – К.: Зодіак – ЕКО, 2002.
4. Бевз Г.П. та інші. Математика: Підручник для 10 – 11 кл. загальноосвітніх навчальних закладів. – К.: Генеза, 2012

Питання  для самоконтролю

1. Яка функція називається показниковою?
2. В яких природних процесах застосовується показникова функція?
3. Чи використовується показникова функція в банківській справі?
4. Яка функція називається логарифмічною?
5. Що називається логарифмічною спіраллю?
6. В яких реальних процесах використовується  логарифмічна функція?

Завдання для самоконтролю ( по групам)

Підготувати доповідь «Використання  показникової та логарифмічної функції в різних науках, техніці і навколишньому середовищі»

 

 

 

 

 

 

 

 

 

 

Структура заняття

 

№	Етап заняття	Методи та форми роботи	Час (хв.)
1	Організаційний етап Мотивація навчальної діяльності	Словесний. пояснювально – ілюстративний,	2
2	Актуалізація опорних знань	Фронтальне опитування, частково – пошуковий. Вправа                                      « Асоціативний кущ»	10
2.1	Систематизація і узагальнення основних відомостей про числові функції.	Словесно-наочний, пояснювально – ілюстративний,
3	Виконання  практичної роботи
3.1	Колективне розв’язування тренувальних вправ	Аналітичний, практичний. Вправа « Мозковий штурм»	5
3.2	Властивості показникової та логарифмічної функцій.	Практична робота	10
3.3	Контроль зворотного зв’язку	Тестовий взаємоконтроль	3
4.	Захист проектів по групам	Метод проектів, словесний, пояснювально – ілюстративний, аналітичний, частково-пошуковий	45
5	Підведення підсумків заняття. Рефлексія.	Словесний, фронтальна бесіда	3
6	Домашнє завдання		2

 

 

 

 

Хід заняття:

 

І. Організаційний момент.  Мотивація навчання.

Викладач. (Привітання зі студентами. Хто відсутній на занятті. Оголошення теми.)

- На сьогоднішньому занятті ми завершуємо вивчення теми  «Показникова та логарифмічна функція ».

-  На початку вивчення теми перед вами були поставлені  проблемні питання : « Де і як застосовується  показникова та логарифмічна функція?»

- Кожна підгрупа  працювала над проектною роботою «Використання показниковою та логарифмічної функції в фізиці‚ техніці‚ хімії‚ біології та інших науках». 

- На сьогоднішньому занятті ми прослухаємо захист ваших проектів.

 

ІІ.  Повторення і узагальнення  матеріалу.

1. Систематизація і узагальнення основних відомостей про числові функції.

- Зараз ми знову поринемо у світ, де є особлива залежність змінної у від змінної х, де у задачах відображене людське буття, тобто у чарівний, цікавий та загадковий світ математики. Ми глибше пізнаємо істину.

 «Немає жодної галузі людського знання, куди не входили б поняття про функції та їх графічне зображення» .                                К. Ф. Лебединцев

 (написати на дошці) Ці слова можуть стати епіграфом нашого заняття.

     -  Серед різноманітних явищ вчені виділили такі, в яких взаємозв’язок величин дуже тісний. Знаючи значення однієї величини, можна визначити значення іншої. З поняттям функції та властивостями деяких функцій ви вже знайомі. Згадаємо і повторимо основні відомості про  функції.

Систематизація і узагальнення основних відомостей про числові функції. (Слайд 2)

• Що називається функцією?

Відповідь. Якщо кожному елементу х множини Х (х є Х) за деяким законом ставиться у відповідність певний елемент у множини у (у є У), тоді говорять, що на множині Х задано функцію у = f(x).

Змінну величину х називають незалежною змінною або аргументом, у –залежною, а літера f позначає закон відповідності.

• Перерахуйте основні властивості функції. (Слайд 3)

Відповідь. Область визначення функції, множина значень функції, способи задання функції, графік функції, нулі функції, парність і непарність, зростання, спадання функції, проміжки знакосталості, найбільше та найменше значення функції.

   ( на екрані по черзі висвітлюється назване)

• Що називається областю визначення функції ?

Відповідь. Множину всіх  значень, яких набуває незалежна змінна (аргумент), називають областю визначення функції і позначають D(f) або D(y).

• Що називається областю значень функції?

Відповідь. Множину всіх значень, яких набуває залежна змінна (функція), називають областю значень функції і позначають Е(f) або Е(у).

• Які способи задання функції ви знаєте?

Відповідь. Функцію можна задавати за допомогою формул, таблиць, графіків.

- Що називається графіком  функції?

Відповідь. Графіком функції називається множина точок координатної площини, абсциси яких дорівнюють значенням аргументу функції, а ординати – відповідним значенням функції.

 -  Взагалі з графіками функцій ми зустрічаємось не тільки на заняттях математики та фізики, але і в повсякденному житті.

- Що таке нулі функції?

Відповідь. Значення аргументу, при яких значення функції дорівнює нулю, називають нулями функції. Щоб знайти нулі функції у = , потрібно розв’язати рівняння = 0.

• Яку  функцію називають парною; непарною?

Відповідь. Функцію у = називають парною, якщо для будь-якого значення х з області її визначення, значення –х теж належить області визначення і виконується рівність  . Графік парної функції симетричний відносно осі у.

      Функцію у = називають непарною, якщо для будь-якого значення х з області її визначення значення –х теж належить області визначення і виконується рівність  . Графік непарної функції симетричний відносно початку координат

• Яку функцію називають зростаючою на проміжку; спадною на проміжку?

Відповідь. Функцію називають зростаючою на деякому проміжку, якщо кожному  більшому значенню аргументу з цього проміжку  відповідає більше значення функції.

         Функцію називають спадною на деякому проміжку, якщо кожному  більшому значенню аргументу з цього проміжку  відповідає менше значення функції.

• Що називають проміжком знакосталості?

Відповідь. Проміжок, на якому функція набуває значень однакового знаку,  називають проміжком  знакосталості функції.

• Знайдіть за графіком нулі функції, проміжки знакосталості та монотонності, найбільше та найменше значення функції.
•  (Слайд )

 

Відповідь.

Нулі функції: -4; 4; 8;

Проміжки знакосталості: (-6; -4); (-4; 4); (4; 8); (8; 10).

Зростає на (-6; 0); (6; 10);  спадає на (0; 6).

Найбільше значення функції 5, найменше значення функції -2.

• Отже, ми повторили основні властивості функцій.

 

 

ІІІ. Виконання практичної роботи (тести)

• Зараз вам буде надано тестові завданняз однією правильною відповідю з даної теми. Через 10 хв. ви обмінюєтеся своїми відповіді і маючи ключ до тестів ( Слайд) перевіряєте один одного. Максимальна кількість балів, яку ви можете отримати-5, тобто 0,5 за кожну правильну відповідь.

ІV Захист проектів. 9 (по групах)

• Ви заздалегідь були поділені на групи «Історики», «Фізики», «Хіміки», « Економісти» та « Географи» і вам було потрібно підготувати проекти та поділитися з іншими студентами: « Як саме використовується показникові та логарифмічна функції в даних науках»?

V. Підведення  підсумка заняття. Рефлексія.

 

• Яка функція називається показниковою?
• В яких природних процесах застосовується показникова функція?
• Чи використовується показникова функція в банківській справі?
• Яка функція називається логарифмічною?
• Що називається логарифмічною спіраллю?
• В яких реальних процесах використовується логарифмічна функція?
• На яких спеціальностях коледжу використовується логарифмічна функція?

•  

 VІ. Домашнє завдання: розв’язати протилежний варіант практичної роботи.

 

• .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТОК А

З історії логарифмів

Логарифм – з грецької  означає “логос”- відношення і “аритмос”-  число. 

Його винахід пов’язаний з двома постатями: швейцарцем Іобстом Бюргі(1552-1632), знаним годинникарем і майстром астрономічних інструментів, і шотландцем Джоном Непером (1550-1617), який теж не був математиком за професією, астрономія була його «хобі». А Бюргі працював разом з астрономом Іоганном Кеплером. Саме величезний обсяг необхідних в астрономії обчислень і спонукав Бюргі і Непера шукати шляхів для їх спрощення. 20 років присвятив Непер своїм логарифмічним таблицям, аби, за його словами, «позбутися нудних і тяжких обчислень, відлякують зазвичай багатьох від вивчення математики». Обидва автори прийшли до своїх таблиць незалежно один від одного. Вони склали таблиці так званих натуральних логарифмів. Бюргі працював над таблицями 8 років і видав їх у 1620 році під назвою «Арифметична і геометрична таблиця прогресії». Проте його таблиці не отримали широкого поширення, бо Непер видав свій «Опис дивовижної таблиці логарифмів» на 6 років раніше. Тому і визнали число e неперовим числом.

 

 

Понад три з половиною сторіччя з тих пір, як у 1614 році були опубліковані Непером перші логарифмічні таблиці, вони вірою і правдою служили астрономам і геодезистам, інженерам і морякам, скорочуючи час на обчислення і, як сказав французький вчений Лаплас , продовжуючи життя обчислювачам.

Ще донедавна важко було уявити собі інженера без логарифмічної лінійки в кишені. Винайдена в 1624 році англійським математиком Едмундом Гунтером , вона дозволяла швидко одержувати відповідь з достатньою для інженера точністю до трьох значущих цифр. І хоч тепер її витіснили калькулятори і комп’ютери, проте можна сміливо сказати, що без логарифмічної лінійки не було і перших комп’ютерів.

      

 

Логарифмічна спіраль

Логарифмічна спіраль – це крива, яка перетинає всі кути, що виходять із однієї точки О, під одним і тим же кутом α.

 

 Рівняння виражається через логарифмічну функцію.

              Таку криву описує рухома точка, відстань від полюса якої росте в геометричній прогресії, а кут, що описується її радіусом-вектором, - в арифметичній.

Характерні особливості логарифмічної спіралі:  

• Має нескінченну кількість витків як при розкручуванні так і при скручуванні;

                 Її називають рівнокутною спіраллю;

• В будь-якій точці спіралі кут між дотичною до неї та її радіус-вектором зберігає               постійне значення;
• Має широке застосування в технічних приладах.
• Властивості цієї кривої так вразили Якоба Бернуллі, що він назвав її spira mirabilis (чудова спіраль) і заповів зобразити її на його могилі з написом Eatemmutata resurgo (перетворювана, відроджуюся знову).

              

 Логарифми в фізиці                               

        Фізика  завжди вимагає математичних розрахунків, тому знання математики у фізиці завжди необхідне. Ось декілька формул, де використовуються логарифми.

 

• Робота, яку виконує газ при ізотермічному процесі

  

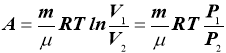
m – маса газу;

µ - молярна маса газу;

R – універсальна газова стала;

Т  – температура за Кельвіном;

V -  об’єм газу;

 

 

• Рівень інтенсивності звуку

  

  - умовно нульовий рівень

                         У техніці часто застосовуються ножі, що обертаються. Сила, з якою вони тиснуть на матеріал, що розрізається, залежить від кута розрізання, тобто кута між лезом ножа і напрямом швидкості обертання. Для того, щоб тиск був сталим, потрібно щоб залишався сталим кут розрізання, а це буде у  тому випадку, коли леза ножів будуть окреслені по дузі логарифмічної спіралі. Завдяки цьому лезо ножа сточується рівномірно.

    Якщо літак буде летіти, дотримуючись весь час одного курсу, тобто перетинаючи всі меридіани під одним і тим самим кутом, то його шлях зобразиться на карті логарифмічною спіраллю.

У гідротехніці по логарифмічній спіралі вигинають трубу, що підводить потік води до турбіни. Завдяки такій формі труби втрати енергії при зміні напряму течії в трубі виявляються мінімальними і напір води використовується з максимальною продуктивністю.

      Логарифми в хімії                                

        Розчини в природі можуть мати різну реакцію середовища: кислу, лужну, нейтральну,що характеризується різною концентрацією йонів Гідрогену С( Н⁺).Для зручності  було введено термін «водневий показник» (рН).

  

З таблиці видно, що різні розчини в людському організмі мають різний рН, його відхилення від норми спричиняє захворювання і навіть загибель організму. Людям з підвищеною кислотністю шлункового соку рекомендується пити мінеральну воду  з вищим рН,а зі зниженою кислотністю - "кислішу" воду(з нижчим рН).

 Використовуючи різні засоби особистої гігієни, креми для шкіри, ліки, необхідно враховувати значення рН. Більшість рідких косметичних засобів має рН 5,5.

   

У сільському господарстві кислотність грунтового розчину є одним із головних чинників, що впливають на врожай. Так, картопля найкраще росте на слабокислих грунтах (рН≈5), а буряк на нейтральних (рН≈7).

       Логарифми в біології                                                

           Можна сказати, що спіраль є математичним символом співвідношення форми і зростання.

 Логарифмічна функція виникає у зв'язку з найрізноманітнішими природними формами. По логарифмічних спіралях розташовуються квітки в суцвіттях соняшника, закручуються раковини молюска Nautilus, роги гірського барана і дзьоби папуг. Один з павуків, епейра, сплітаючи павутиння , закручує нитки навколо центра по логарифмічним спіралям.

       

Нічні метелики, які пролітають величезні відстані, орієнтуючись по паралельним промінням місяця, інстинктивно зберігають прямий кут між напрямом руху і променем світла. Якщо вони орієнтуються на точкове джерело світла, інстинкт їх підводить, і метелики потрапляють в полум’я по логарифмічної спіралі, що скручується.

              Логарифми в музиці                                                  

         Піфагор був не тільки великим математиком, а й хорошим музикантом. Він встановив, що приємні сполучення звуків відповідають певним співвідношенням між довжинами струн, що коливаються, або відстаням між дірочками сопілки. Саме він створив першу математичну теорію музики, і хоча музиканти не дуже люблять перевіряти „алгеброю гармонію”, вони весь час мають справу з математикою, бо сучасна гама ґрунтується на логарифмах.

         Номери клавіш рояля являють собою логарифми кількості коливань відповідних звуків. Номер октави – характеристика ( тобто ціла частина) логарифма, а номер звука в даній октаві - його мантиса ( тобто дробова частина).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТОК В

З ТЕМИ: « Застосування показникової та логарифмічної функцій»

	14.03	16.03	21.03	23.03	28.03	30.03	04.04	06.04	11.04
	Від 0-2 балів								Пр.роб.	Доповіді
									1-5 б.	1-5 б.
Виконання  д\з і СРС
Робота на занятті
Всього

                                                

 Бал    _________________

 

 

 

 

 

 

 

 

 

 

 

                       

                          

 

 

ДОДАТОК С

ТЕСТОВІ ЗАВДАННЯ

«ЛОГАРИФМІЧНА ТА ПОКАЗНИКОВА ФУНКЦІЇ»

Варіант- І

1. Із наведених нижче функцій показниковою є:

а) y = x²;   б) y = ()^x;      в) y = 12,4 – x;  г) y = .

2. Із наведених нижче функцій спадною показниковою є:

а) f (x) = 3^x;  б) f(x) =        в) f(x) = ;  г) f(x) = .

3. Із наведених нижче функцій зростаючою показниковою є:

а) f(x) = ;  б) f(x) = ()^x;        в) f(x) = ;  г) f(x) =

4. Якщо 3^m < 3ⁿ, то виконується умова:

а) m < n;   б) m > n;       в) m = n;   г) m n.

5. Якщо 4^k > 4^l, то виконується умова:

а) k < l;   б) k > l;       в) k = l;       г) k l.

6. Розв’яжіть рівняння 3^x-2 = 9.

а) x = 4;   б) x = 2;      в) x = 0;    г) x = 1.

7. Обчислити log 25.

а) ;   б) ;          в) -2;    г) 2.

8. Обчислити log 9.

а) -3;    б) ;      в) 3;    г) 2.

9. logx = -2. Знайти х.

а) ;    б) ;              в) -4;    г) 2.

10. log3 = x. Знайти x.

а) ;    б) 1;              в) -1;      г) 0.

ТЕСТОВІ ЗАВДАННЯ

«ЛОГАРИФМІЧНА ТА ПОКАЗНИКОВА ФУНКЦІЇ»

Варіант- ІІ

1. Із наведених нижче функцій показниковою є:

а) y = x⁴;   б) y = 12,4 – x;         в) y = 3^x;             г) y = .

2. Із наведених нижче функцій спадною показниковою є:

а) f (x) = 3^x;           б) f(x) =0,5^х;      в) f(x) =   г). f(x) =

3. Із наведених нижче функцій зростаючою показниковою є:

а) f(x) = ;  б) f(x) = ()^x;      в) f(x) = ;  г) f(x) =

4. Якщо 4^m < 4ⁿ, то виконується умова:

а) m n;   б) m = n;   в) m > n;            г) m < n.

5. Якщо( ^k > ( ^l, то виконується умова:

а) k = l;   б) k > l;          в) k < l;    г) k l.

6. Розв’яжіть рівняння 3^x-2 =27.

а) x = 4;   б) x = 5;         в) x = 0;     г) x = 1.

7. Обчислити log0,5  25.

а) ;   б) ;          в) -2;    г) 2.

8. Обчислити log 27.

а) -3;    б) ;                в) 3;    г) 2.

9. logx = -1. Знайти х.

а) ;    б) ;      в) -4;    г) 2.

10. log ₃ 3 = x. Знайти x

а) ;    б) 1;              в) -1;    г) 0.

ДОДАТОК D

КЛЮЧ ДО ТЕСТІВ

 

 

ВАРІАНТ- І	ВАРІАНТ-ІІ
Б	В
Б	Б
Б	Б
А	Г
Б	Б
А	Б
Г	В
Г	В
А	Б
В	Б