стаття "МЕТОДИКА ВИВЧЕННЯ ТЕМИ «ПОДІБНІ ТРИКУТНИКИ»"

Про матеріал

Розроблена методика з вивчення теми «Подібність трикутників» з використанням інформаційно-комунікаційних технологій дозволяє: зробити навчання цікавим; розширити можливості візуалізації навчального матеріалу; індивідуалізувати процес навчання; здійснювати моніторингові відстеження якості засвоєння учнями навчального матеріалу; створити комфортні психологічні умови для учнів; здійснювати самостійну навчально-дослідницьку діяльність учнів. Перспективу подальших наукових досліджень вбачаємо в розробці методики вивчення теми «Геометричні перетворення» з використанням інформаційно-комунікаційних технологій.

Перегляд файлу

К. І. Васильєв

УДК 373.5.016:514]:004

МЕТОДИКА ВИВЧЕННЯ ТЕМИ «ПОДІБНІ ТРИКУТНИКИ»

Анотація. У статті наведено методичні рекомендації вивчення теми «Подібність трикутників» в курсі геометрії основної школи з використанням інформаційно-комунікаційних технологій. Проведено порівняльний аналіз представлення даної теми в діючих підручниках геометрії згідно нового Державного стандарту.

Ключові слова: подібність трикутників, підручник геометрії, інформаційно-комунікаційні технології.

Summary. The article gives methodical recommendations for the study of the topic of "Similarity of triangles" in the course of geometry at schools, using information and communication technologies. A comparative analysis of the presentation of this topic in the current textbooks of geometry according to the new State Standard was conducted.

Keywords: similarity of triangles, textbook of geometry, information and communication technologies.

Постановка проблеми. Впровадження сучасних інформаційно-комунікаційних технологій (ІКТ) навчання є пріоритетним напрямком розвитку освіти, тому сучасна комп'ютерна освіта має стати складовою частиною становлення особистості, дати учневі внутрішній імпульс для розвитку.

Використання поняття подібності трикутників в курсі геометрії основної школи має велике методичне значення:

- ідея подібності трикутників дає ефективний метод розв’язування великого класу задач на доведення, побудову, обчислення;

- доведення теорем із залученням подібності значно простіше доведень, заснованих на ознаках рівності трикутників. У більшості випадків ці доведення не пов'язані з допоміжними побудовами, виконання яких викликає значні труднощі в учнів;

- реалізація ідеї подібних трикутників у навчанні сприяє формуванню наукового світогляду в учнів.

Часті зміни навчальних програм призвели до того, що тема «Подібність трикутників» мало вивчена в методичному плані і теми, пов'язані з подібністю в шкільних підручниках викладаються по-різному. Внаслідок чого, методика вивчення подібних трикутників вимагає постійного вдосконалення.

Аналіз актуальних досліджень. Методичні особливості вивчення геометрії висвітлені в працях Г. П. Бевза, В.Г. Бевз, М. І. Бурди, О. С. Дубинчук, Т. В. Крилової, Ю. І. Мальованого, З. І. Слєпкань, Н. А. Тарасенкової, О. С. Чашечникової, В. О. Швеця, М. І. Шкіля та ін. Деякі публікації присвячено питанню формування геометричних умінь, а саме: конструктивно-графічних та вимірювальних (Т.П. Гора, А.А. Мазаник та ін.), оперування геометричними поняттями (В.М. Осинська, Т.І. Тітова, Л.Г. Філон та ін.), доведення геометричних тверджень (Р.І. Загоруй, А.М. Капіносов та ін.)

Мета статті полягає у розробці методичних рекомендацій вивчення теми «Подібність трикутників» в курсі геометрії основної школи з використанням інформаційно-комунікаційних технологій.

Виклад основного матеріалу.

У чинній програмі з математики [5] тема «Подібність трикутників» залишається однією з основних тем курсу геометрії. На її вивчення відведено 14 годин у 8 класі, хоча залежно від обраного підручника часові рамки теми можуть несуттєво змінюватися.

Розглянемо як представлена тема «Подібність трикутників» в діючих підручниках з геометрії авторських колективів: А.Г. Мерзляк, В.Б. Полонський, М.С. Якір [4]; А.П. Єршова, В.В. Голобородько, О.Ф. Крижановський, С.В. Єршов [2]; М.І. Бурда, Н.А. Тарасенкова [1].

Для зручності подання матеріалу використовуватимемо лише прізвище першого автора, не зменшуючи вкладу інших авторів підручника в його створення.

У трьох підручниках вивчення теми «Подібність трикутників» починається з вивчення різних тем. Структуру подання теми представимо у таблиці 1.

Таблиця 1

Структура вивчення теми «Подібність трикутників» у діючих підручниках геометрії

А.Г. Мерзляк	А.П. Єршова	М.І. Бурда
Теорема Фалеса. Теорема про пропорційні відрізки (властивості медіани і бісектриси трикутника)	Узагальнена теорема Фалеса	Подібні трикутники
Подібні трикутники	Означення подібних трикутників	Узагальнена теорема Фалеса
Перша ознака подібності трикутників (властивість хорд, що перетинаються; властивість дотичної та січної)	Ознаки подібності трикутників: - подібність трикутників за двома кутами; - подібність трикутників за двома сторонами і кутом між ними; - подібність трикутника за трьома сторонами.	Перша ознака подібності трикутників
Друга та третя ознаки подібності трикутників	Подібність прямокутних трикутників: - ознаки подібності прямокутних трикутників; - пропорційні відрізки в прямокутному трикутнику.	Друга та третя ознаки подібності трикутників
Метричні співвідношення у прямокутному трикутнику	Теорема Піфагора та теорема обернена до неї	Середні пропорційні у прямокутному трикутнику (властивість бісектриси)
Теорема Піфагора	Перпендикуляр і похила	Теорема Піфагора. Перпендикуляр і похила
	Застосування подібності трикутників: - властивість бісектриси трикутника; - метричні співвідношення у колі; - метод подібності.

Як бачимо зі структури представленої в таблиці 1 тема «Подібність трикутників» вивчається по різному.

Наприклад, властивості медіан і бісектрис трикутника в підручнику А.Г. Мерзляка подаються на початку вивчення теми, на відміну від підручника А.П. Єршової, де ці властивості представлені в самому кінці вивчення теми, а в підручнику М.І. Бурди ці теореми учні мають довести самі, бо вони представлені в якості задач для розв’язування.

Тому існує і відмінність у доведенні цих властивостей: у першому випадку використовуються ознаки подібності прямокутних трикутників, а в другому – теорема про пропорційні відрізки (Узагальнена теорема Фалеса).

Теорема (властивість бісектриси трикутника). Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні прилеглим сторонам.

Доведення (за підручником А.П. Єршової [2, с. 136])

Рис. 1

Нехай – бісектриса трикутника . Доведемо, що .

У випадку, коли , твердження теореми очевидне, оскільки бісектриса водночас є і медіаною.

Розглянемо випадок, коли .

Проведемо перпендикуляри і до прямої (рис. 1). Прямокутні трикутники і подібні, оскільки їх гострі кути при вершині рівні як вертикальні.

Із подібності цих трикутників маємо: . З іншого боку, прямокутні трикутники і також подібні, оскільки мають рівні гострі кути при вершині . Звідси випливає, що . Прирівнюючи цю рівність із попередньою, отримуємо: , що і треба було довести.

Доведення (за підручником А.Г. Мерзляка [4, с. 79])

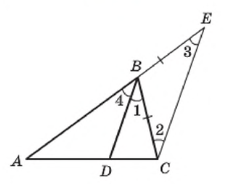
Рис. 2

На рисунку 2 – бісектриса трикутника . Доведемо, що .

Через точку С проведемо пряму, паралельну прямій . Нехай проведена пряма перетинає пряму АВ в точці Е. Кути 1 і 2 рівні як різносторонні при паралельних прямих і СЕ та січній ВС; кути 3 і 4 рівні як відповідні при паралельних прямих і СЕ та січній АЕ. Оскільки  бісектриса трикутника , то . Звідси . Тоді трикутник рівнобедрений з рівними сторонами і . За теоремою про пропорційні відрізки . Оскільки , то .

Підхід до доведення ознак подібності трикутників у всіх трьох підручниках однаковий. На їх основі можна довести багато цікавих і важливих властивостей геометричних фігур. Йдеться про властивості прямокутного трикутника, відрізків у колі і т. ін.

Також у якості опорних задач представлені властивості подібних трикутників:

- відношення периметрів подібних трикутників дорівнює коефіцієнту подібності;

- відношення відповідних лінійних елементів (бісектрис, медіан, висот тощо) подібних трикутників дорівнює коефіцієнту подібності;

- відношення площ подібних трикутників дорівнює квадрату коефіцієнта подібності.

Перш ніж доводити ознаки подібності трикутників, доцільно звернути увагу учнів, що ці доведення виконуються за однаковою схемою. Проілюструвати цю схему можна на доведенні І ознаки. Це дасть можливість залучити учнів до колективного доведення двох інших ознак [6, с. 302]

У підручнику М.І. Бурди наведено алгоритми доведення подібності двох трикутників за означенням та ознаками.

Ознаки подібності прямокутних трикутників наведені в підручнику М.І. Бурди в якості задач (виділених жирним шрифтом), які учні мають довести самостійно, а в підручнику А.П. Єршовою вони доведені у підручнику.

В усіх підручниках досить великий задачний матеріал. Серед задач зустрічаються практичні, дослідницькі, розв’язання яких сприяє формуванню ключових та предметних компетентностей учнів. Також наведені зразки їх розв’язань, що автори пропонують брати за еталон.

Окремим параграфом у підручнику А.П. Єршової виокремлено «Метод подібності». У ньому наведено план розв’язання задач на побудову методом подібності. В цьому ж підручнику є додатки, в одному з яких наведено доведення узагальненої теореми Фалеса, а в іншому – відомості про золотий переріз.

У рубриці «Дізнайтеся більше» підручника М.І. Бурди представлені відомості про пряму Ейлера, в цій же рубриці представлено доведення узагальненої теореми Фалеса. Подібна рубрика є і у підручнику А.Г. Мерзляка там представлені з доведенням теореми Менелая та Птолемея.

У підручнику А.П. Єршової наведена тематика рефератів до розглядуваної теми. Крім цього до підручника є електронний додаток, що розміщений на сайті interactive.ranok.com.ua. На даному сайті можна пройти онлайн-тестування для перевірки знань учнів.

В кінці параграфів кожного з підручників наведено питання для самоконтролю, задачі для підготовки до контрольної роботи.

Використання ІКТ може супроводжувати такі види навчальної роботи з теми «Подібність трикутників», як:

а) написання рефератів на задану тему («25 доведень теореми Піфагора», «Золотий переріз» тощо),

б) збір матеріалу по темі (знаходження доведення властивостей подібних трикутників, теореми Піфагора, Менелая тощо),

в) ілюстрування своїх текстів матеріалами з Інтернету (проведення експериментальних досліджень з теми «Подібність трикутників», наприклад з використанням Geogebra тощо).

«Бібліотека електронних наочностей «Геометрія, 7-9 клас» – це електронне видання, що містить набір мультимедійних компонентів, які відображають об’єкти геометрії, які вивчаються в 7-9 класах; програвач мультимедійних компонентів; простий у використанні редактор, що дозволяє вчителю формувати набори необхідних наочностей [3, с. 102]. Для проведення уроку з теми «Подібність трикутників» можна використати необхідні електронні наочності з даного видання чи провести опитування за даним набором запитань. Їх можна вставити і до вчительської мультимедійної презентації.

Мультимедійну презентацію для вивчення теми «Подібність трикутників» можна використовувати для:

пояснення нової теми чи повторенні вивченого з метою унаочнення пояснювального матеріалу;
робота з усними вправами для економії навчального часу;
демонстрація умови й розв’язання задач, геометричних креслень;
взаємоперевірка самостійних робіт за допомогою висвітлення відповідей на слайді;
проведення тестування, фізкультхвилинок, рефлексії;
демонстрація портретів математиків і розповідь про їхні відкриття;
ілюстрація практичного застосування теорем у житті;
створення учнями комп'ютерних презентацій до уроків узагальнення й систематизації знань і способів діяльності;
позакласної роботи: математичні ігри й вечори тощо.

Висновки. Розроблена методика з вивчення теми «Подібність трикутників» з використанням інформаційно-комунікаційних технологій дозволяє: зробити навчання цікавим; розширити можливості візуалізації навчального матеріалу; індивідуалізувати процес навчання; здійснювати моніторингові відстеження якості засвоєння учнями навчального матеріалу; створити комфортні психологічні умови для учнів; здійснювати самостійну навчально-дослідницьку діяльність учнів. Перспективу подальших наукових досліджень вбачаємо в розробці методики вивчення теми «Геометричні перетворення» з використанням інформаційно-комунікаційних технологій.

Список використаних джерел