Урок - конференция на тему: «Прямоугольная система координат на плоскости»

 

Урок - конференция

 

Тема: «Прямоугольная система координат на плоскости»

Цели урока:

• Образовательные:

обобщение знаний и умений учащихся по теме «Координатная плоскость», промежуточный контроль за знаниями и умениями учащихся.

Развивающие:

развитие коммуникативной деятельности учащихся, развитие логического мышления, активизация работы учащихся на уроке за счет вовлечения их в игру, развитие интереса учащихся к предмету посредством нетрадиционной формы ведения урока. Развитие математически грамотной речи, кругозора учащихся. Развитие умения самостоятельной работы с дополнительной литературой.

Воспитательные:

воспитание познавательной активности, чувства ответственности, культуры общения. Воспитание чувства сопереживания и взаимовыручки, чувства ответственности друг за друга. Воспитание аккуратности при выполнении построений.

Тип урока: урок изучения нового материала

Вид урока: урок-конференция

Оборудование: презентация к уроку, творческие проекты учащихся,

 

Ход урока:

Организация начала урока

Учитель:

Друзья мои, приветствую я вас.

 Звенит звонок,

 Мы вместе начинаем наш урок.

– Сегодня мы с вами встречаем на уроке гостей и должны показать, как мы умеем чётко и слажено работать. Причем работать мы будем в команде. Не надо волноваться, у нас с вами всё получится. Хочу пожелать себе и вам успехов и хорошего рабочего настроения.

Эпиграфом сегодняшнего урока могут стать слова  французского математика и астронома  Пьера - Симона Лапласа: «То, что мы знаем – ограничено, а то, что мы не знаем – бесконечно…»

Надеюсь, что сегодня на уроке каждый из нас сделает для себя хотя бы маленькое открытие.

 

Мотивация учебной деятельности

   Учитель:

  У каждого человека бывают ситуации, когда  необходимо определить свое или чьё-то местонахождение, к примеру найти  по билету место в  зрительном зале или в вагоне поезда,  определить местонахождение того или иного здания,  дома,  квартиры. Мы нередко можем слышать такую фразу «Оставьте мне ваши координаты».  Что означает это выражение для простого человека и для математика? (ответы учеников) На первый взгляд ваш собеседник  просит у вас либо адрес, либо номер телефона.  А с точки зрения математики вас  просят указать  координаты некоторой  точки.

Сегодня мы с вами будем говорить о прямоугольной системе координат, с которой уже имели дело и в курсе математики 6 класса, и в курсе алгебры при построении графиков функций. Но в курсе геометрии сегодня мы приступаем к изучению новой темы «Декартовы координаты на плоскости». И поэтому  предлагаю сегодня провести урок конференции, к которой подготовили свои выступления:

•          Секция теоретиков с темой «Толкование происхождения слов, связанных с декартовой системой координат»
•          Секция историков с темой «История возникновения  системы координат»
•          Секция практиков  с темой «Где же в жизни мы встречаемся с прямоугольной системой координат?»
•          Секция искусствоведов с темой «Декартовы координаты в живописи»

Результаты работы участников секций руководители по ходу урока будут фиксировать в оценочных листах.  Участники готовы? Тогда конференцию по теме  «Прямоугольная система координат на плоскости» объявляю открытой.

 

Выступление секций с докладами своей работы.

Учитель:

У каждого исследователя  бывает желание, прежде чем приступить к изучению темы,  узнать толкование  и происхождение тех слов, которые  используются в изучаемой теории. Поэтому первыми  свою работу представят ребята из секции теоретиков, которые нам  расскажут о происхождении  слов, связанными с декартовыми координатами, а также напомнят особенности ее построения.

Выступление секции теоретиков с темой «Толкование происхождения слов, связанных с декартовой системой координат»:

Слово «система» греческого происхождения: «тема»  — нечто заданное, «сис»  —  составленное из частей. Таким образом, «система» - нечто заданное, составленное из частей (или четко расчлененное целое).

Положение точки на плоскости задаётся двумя числами, координатами. Термин «координаты» произошёл от латинского слова -  «упорядоченный». Чтобы определить положение точки на плоскости, надо построить прямоугольную систему координат. Как это делать, мы сейчас и выясним.

- Постройте горизонтальную прямую.

- Постройте вертикальную прямую так, чтобы она пересекала данную прямую под прямым углом.

- Превратим эти прямые в координатные. Для этого определим положительное направление, укажем начало отсчета, выберем единичный отрезок.

- Положительное направление задаётся стрелочкой на каждой прямой: на горизонтальной прямой положительное направление выбирается «слева направо», на вертикальной – «снизу вверх».

- Точку пересечения этих прямых обозначим буквой О. Называется точка О –началом координат. Эта буква выбрана не случайно, а по сходству с цифрой 0.

- Выбираем единичный отрезок. За единичный отрезок можно принять длину одной, двух клеток и более. Главное правило, что единичный отрезок на каждой прямой, один и тот же, либо одна клетка, или две клетки и. д.

- Дать название этим прямым. Горизонтальную прямую обозначаем x. Называется осью абсцисс. Вертикальную прямую обозначаем y, называется осью ординат. Вместе эти две прямые называются системой координат. (Ребята, работая в тетрадях, подписывают каждую прямую.)

Термины «абсцисса» и «ордината» (образованные от латинских слов «отсекаемый» и «упорядоченный») были введены в 70-80 гг. XVII в. немецким математиком Вильгельмом Лейбницем.

Итак, алгоритм построения системы координат:

1. Строим горизонтальную прямую.

2. Строим вертикальную прямую, перпендикулярно первой.

3. Задаём положительное направление стрелками.

4. Обозначаем точку пересечения О.

 5. Указываем единичный отрезок.

Плоскость, на которой задана система координат, называется координатной плоскостью. Ваш тетрадный листок стал моделью координатной плоскости.

- На сколько частей разделили прямые Ох и Оу плоскость? (На четыре) Эти части называются координатными четвертями. Их нумеруют против часовой стрелки римскими цифрами.

Для нахождения координат точки надо:

• Опустить  из точки  перпендикуляр на ось х.
• Найти точку пересечения этого перпендикуляра с осью х.
• Опустить из точки  перпендикуляр на ось у.
•  Найти точку пересечения этого перпендикуляра с осью у.
• Записать координаты точки в круглых скобках. На первое место поставить значение х, на второе – значение у

На данном рисунке каковы координаты точек? (ответы учащихся)

К(4; 2), D(-3; 6), С(-2;0), Е(-7; -5), В(6; -7).

Задание для участников конференции: Постройте на вашей системе координат точки А(5; 4), В(3; 3), С(-3; 3), D(-3; -2). Затем сверим с оригиналом.

   Участники секции теоретиков демонстрируют буклет по данной теме. 

 

Учитель:

      История возникновения координат и системы координат начинается давно, первоначально идея метода координат возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи. Изображать числа в виде точек, а точкам давать числовые обозначения было желанием ещё античной геометрии, связанное с потребностью сопоставлять положение светил на небе и определенных пунктов на поверхности Земли. О том, какова же история появления теории системы координат, расскажут нам представители секции истории.

Выступление секция истории с темой «История возникновения  системы координат»:

Идея координат, т. е. задавать положение точки на плоскости с помощью чисел, зародилась в древности. Первоначальное их применение связано с астрономией и географией, с потребностью определить положение светил на небе, при составлении календаря, географических и звёздных карт.

Во II веке древнегреческий учёный Клавдий Птолемей занимался изучение движения небесных тел. Он пользовался широтой и долготой в качестве координат для описания астрономических явлений.

Французские математики Пьер Ферма и Рене Декарт в XVII веке впервые открыли значение использования метода координат в математике. Ферма в более систематической форме, чем Декарт, развил метод координат. Декарт впервые опубликовал изложение метода координат в книге «Геометрия», поэтому прямоугольную систему координат часто называют декартовой. Декарт   считается  одним   из   основателей   новой   математики – аналитической геометрии.  Его  имя  сохранили   термины:  «декартовы   координаты»,   «декартов   лист»,  «правило  знаков   Декарта»,   «метод   неопределенных   коэффициентов  Декарта».

Существует легенда: «Однажды в незнакомый город приехал молодой Декарт. Его ужасно мучил голод. Стоял промозглый месяц март. Решил к прохожей обратиться Декарт, пытаясь дрожь унять: Где тут гостиница, скажите? И дама стала объяснять: – Идите до молочной лавки, потом до булочной, за ней Цыганка продает булавки и яд для крыс и для мышей, а дальше будут магазины, найдете в них наверняка сыры, бисквиты, фрукты и разноцветные шелка… Все объяснения эти слушал Декарт, от холода дрожа. Ему хотелось очень кушать. Но звонкий голос продолжал: – За магазинами – аптека (аптекарь там – усатый швед), и церковь, где в начале века венчался, кажется, мой дед…  Когда на миг умолкла дама, вдруг произнес ее слуга: – Идите три квартала прямо. И два направо. Вход с угла».  Как вы думаете, удалось ли Декарту найти гостиницу по данному описанию? Возможно,  именно этот случай и сподвиг Декарта к созданию прямоугольной системы координат. И с решением такой задачи он блестяще справился.

Интересен тот факт, что Рене Декарт увлекался не только математикой как наукой. Он увлекался науками от медицины до метеорологии. Его многочисленные труды были посвящены философии, астрономии,  психологии, физиологии, физике и другим наукам. Декарт первый математически вывел закон преломления света на границе двух различных сред. Точная формулировка этого закона позволила усовершенствовать оптические приборы, которые тогда стали играть огромную роль в астрономии и навигации.

Великий физиолог И. П. Павлов поставил памятник-бюст   Рене Декарту возле своей лаборатории (Колтуши), потому что считал его предтечей своих исследований.

 

 

 

Задание для участников конференции: Разгадав кроссворд, найти ключевое слово. (Участники секции историков демонстрируют газету по данной теме. 

1
	2
		3
	4
5
	6

Вопрос:

1. Координата точки.
2. Части, на которые координатные прямые делят координатную плоскость.
3. В переводе с латинского «упорядоченный».
4. Точка пересечения координатных прямых – это… отсчета.
5. Французский математик  XVII века.
6.  Древнегреческий учёный II века.

 

Проверка:

1     О	Р	Д	И	Н	А	Т	А
	2      Ч	Е	Т	В	Е	Р	Т	Ь
		3      К	О	О	Р	Д	И	Н	А
	4   Н	А	Ч	А	Л	О
5   Ф	Е	Р	М	А
	6     П	Т	О	Л	Е	М	Е	Й

 

 

Гимнастика для глаз

  Мы немного отвлечемся

  И гимнастикой займемся.

  С места не вставая,

  Головой не вращая.

    Чтоб глаза твои зоркие были,

 Чтоб в очках тебе не ходить,

 Эти лёгкие движенья

        Предлагаю повторить.(глазами следим за движением бабочки)

 

Учитель:

Говоря о математике как науке нельзя ещё раз не вспомнить слова великого Рене Декарта «Математика – мощный и универсальный  метод познания природы, образец для  других наук». Системы координат пронизывают всю практическую жизнь человека и находят свое практическое применение.  Вы скажете,  что этого не может быть. Вот изучили систему координат  на уроках геометрии и все на этом.  Однако это не так.  И именно с этим вопросом обратимся  к отделу практиков.  О том, где находит свое применение система координат, расскажут нам представители этой секции.

Выступление секция практиков с темой «Где же в жизни мы встречаемся с прямоугольной системой координат?»

Информатика. Рисунки, схемы, чертежи, графики – графические формы представления информации. Метод кодирования – это один из удобных способов представления числовой  информации с помощью графиков, которые строятся в различных системах координат.

Биология. Построение схем молекул ДНК, построение диаграмм и графиков, прослеживающих эволюцию развития. Экологические проблемы и проблемы биосферы все эти вопросы рассматриваются при помощи  различных систем.

Физика. Координатная система нужна, чтобы определить взаимное расположение – координацию – тел в пространстве.

Военное дело. Системы координат применяются для  составления карт местности, разработки военных стратегий, и тактики.

Экономика. Разнообразные системы координат применяются для  построения графика спроса и предложения, при графическом изображении разнообразных зависимых  величин.

Медицина. В медицине используют координатную систему, в кардиологии - снимают кардиограмму. Делают анализы, готовят различные лекарства. Проведение медицинских исследований – флюорография, разнообразные снимки органов.  В области хирургии - лазерные операции.

Астрономия. Расположение звезд на небе, составление карт. Запуски спутников и космических кораблей, любые виды прогноза основываются  на  применение различных  систем  координат.

Машиностроение. В машиностроении нельзя обойтись без системы координат, ведь прежде, чем что-то создать необходимо, сделать чертеж, а он строится по координатам на определенной системе.

География. Примером системы отсчета, естественной  для городского человека, служит искусственное образование – сам город. Город – это одно большое тело, внутри и относительно которого можно определить место любого малого тела, установив его, так сказать, внутренний «адрес». Местоположение любого объекта на поверхности Земли, его «адрес», определяется географической широтой («адрес» по горизонтали) и географической долготой («ад­рес» по вертикали). Следовательно, чтобы установить положение объекта на Земле  нужно сначала понять, в каком полушарии находится объект, затем по числам широты и долготы найти соот­ветствующие параллель и меридиан и, наконец, определить точку их пересечения, в которой и будет находиться объект.

Задание: Работа с административной картой Украины для определения географических координат городов страны. По координатам определить  города  Украины.

 

 

	Долгота	Широта	Город
1	30°30'в.д.	50° 27' с.ш.
2	24°00' в.д.	49°50' с.ш.
3	37°48' в.д.	48°00' с.ш.
4	34°6' в.д.	44°56' с.ш.

 

Ответы:  1.-Киев,  2.- Львов, 3.-Донецк, 4.- Симферополь.

 

Учитель:

   Вполне уместным  является вопрос:  А есть ли такие области, где не используется наследие Рене Декарта?  И, конечно же, простой обыватель может с уверенностью сказать: конечно – это же элементарно, искусство – вот та область, для которой имя Декарта  осталось неизвестным. Однако вы поторопились!

 «В чистой математике живет всегда художник: архитектор и даже поэт». И, наверное, не зря заявку на участие в научно-практической конференции  подали участники секции искусствоведов, которые работали по теме «Декартовы координаты в живописи».

Выступление секция искусствоведов с темой «Декартовы координаты в живописи»

Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта. В погребальной камере пирамиды отца Рамсеса на стене имеется сеть квадратиков.  С  их помощью перенесено изображение в увеличенном виде. Прямоугольной сеткой пользовались и художники Возрождения.
                            

Слово «перспектива» в переводе с латинского означает «ясно вижу». В изобразительном искусстве линейная перспектива — это изображение предметов на плоскости в соответствии с кажущимися изменениями их величины. Основу современной теории перспективы заложили великие художники эпохи Возрождения — Леонардо да Винчи, Альбрехт Дюрер и другие. На одной из гравюр Дюрера изображён способ рисования с натуры через стекло с нанесённой на него квадратной сеткой. Этот процесс можно описать так: если встать перед окном и, не изменяя точки зрения, обвести на стекле всё, что видно за ним, то полученный рисунок и будет перспективным изображением пространства.

Египетские методы проектирования, которые, похоже, основывались на схемах квадратной сетки. В египетском искусстве имеются многочисленные примеры, показывающие, что художники и скульпторы сначала рисовали сетку на стене, которую предстояло расписать или вырезать, для того чтобы сохранить установленные пропорции. Простые числовые отношения этих сеток служат сердцевиной всех великих художественных произведений египтян.

Тот же метод использовался многими художниками Возрождения, в том числе и Леонардо да Винчи. В Древнем Египте это нашло свое воплощение в Великой пирамиде, что и подкрепляется ее тесной связью с узором на Марлборо-Дауне.

Приступая к работе, египетский художник расчерчивал стену сеткой прямых линий и затем тщательно переносил на нее фигуры. Но геометрическая упорядоченность не мешала ему воссоздавать натуру с детальной точностью. Наружность каждой рыбы, каждой птицы передана с такой правдивостью, что современные зоологи без труда определяют их виды. На рисунке дана деталь композиции с иллюстрации - дерево с птицами, схваченными сетью Хнумхотепа. Движение руки художника направлялось не только запасами его навыков, но и глазом, чувствительным к очертаниям натуры.

 Задание: Этот знак в школе Пифагора считался символом дружбы, он был чем-то вроде талисмана, которым одаривали друзей, тайным знаком, по которому пифагорейцы узнавали друг друга. В средние века он предохранял от нечистой силы, что, впрочем, не мешало называть его «Лапой ведьмы».

Постройте рисунок на координатной плоскости,  последовательно соединив точки:

А ( 0; 3 ), В ( -1; 1), С (-3; 1), D (-1; 0), Е ( -2; -2), F (0; -1), G (2; -2), К ( 1;0 ), L (3; 1), М (1; 1 ), А ( 0; 3). Учащиеся выполняют задание самостоятельно с последующей проверкой на экране.             

 

 

 

Самостоятельная работа. Тестирование.

Тест по теме «Декартова система координат»

1. Координатные прямые называются координатными ... .

А) лучами; В) линиями; С) осями; D) аргументами; Е) параллелями.

2. Плоскость, на которой выбрана система координат, называется ... .

А) простынью;  В) скатертью; С) системой; D) координатной областью;

Е) координатной плоскостью.

3. Найдите координаты точки С — одной из вершин прямоугольника ABCD.

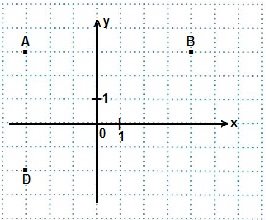
A) C (4; -2);  B) C (-3; -2);  C) C (-2; 4);  D) C (4; 3);   E) C (-3; 3).

4. Место точки на координатной плоскости определяется ... .

А) парой чисел;   В) тройкой чисел; С) одним или двумя числами;

D) самой точкой;  Е) абсциссой точки.

5. Абсцисса и ордината заданной точки называются ... точки.

А) адресом; В) координатами; С) аппликатой; D) установкой; Е) местоположением.

6. Оси координат разбивают плоскость на четыре части, которые называются ...

А) частями плоскости; В) областями плоскости; С) координатными четвертями;

D) координатными плоскостями;  Е) четвертными плоскостями.

 

Верные ответы к тесту:

1-С;  2-Е;  3-А;  4-А;  5-В;  6-С.

 

Подведение итогов урока. Рефлексия

Что ж, пора подвести итоги нашей работы на уроке. Ребята, цели урока достигнуты? Слово руководителям секций. (выступления учащихся, выводы по уроку) Принцип «Незаконченное предложение»:

• Что дал мне сегодняшний урок?
• Что дала мне работа в группах?
• Какие трудности  встретились? Как с ними справились?
• Что нового я узнал на уроке?
• Каким образом я смогу полученные на уроке знания использовать в будущей жизни?

Заполнение графы в оценочном листе: Мы молодцы потому, что-

Теперь подсчитайте среднее арифметическое и поставьте получившуюся оценку в соответствующую графу.

 

Домашнее задание: 

Решить № 286, 289, 290.   Прочитать п. 8(стр.79)

Творческое задание:

• Написать доклад или сделать презентацию о великих ученых: Гиппархе, Птолемее, Декарте; о различных системах координат.
• Составить кроссворд по теме «Координатная плоскость».
• На листе А4 изобразить по координатам любимое животное, созвездие.

Творчество и фантазия только приветствуются.

 

Закончить  сегодняшнюю конференцию «Прямоугольная система координат на плоскости» я хочу словами  Омара Хайяма: «Изучив столько всего, лишь теперь, уразумел я, что на самом деле не знаю ничего…» 

 - Как выдумаете, почему именно эти строки завершают  сегодняшний урок?

Действительно, геометрия - это наука точная в рассуждениях, безупречная в доказательствах, ясная в ответах, гармонично сочетающая в себе прозрачность мысли и красоту человеческого разума.

Геометрия до конца не изученная наука, и,  может быть,  многие открытия ждут именно вас!

 Окончен урок, и выполнен план.

 Спасибо, ребята, огромное вам.

 За то, что упорно и дружно трудились,

 И знания точно уж вам пригодились.

 

 

Оценочный лист секции____________________9-Б класса.  Дата___________

№	Ф.И. ученика	Прог-ноз	Подго-товка (5б.)	Построе -ние точек (3б.)	Крос- сворд  (2б.)	Карта (3б.)	Рисунок (3б.)	Тест (3б.)	Рабо- та в груп -пе(3б.)	Само-оцен-ка	Оцен-ка за урок (24:2)
1
2
3
4
5
6
Мы молодцы потому, что-