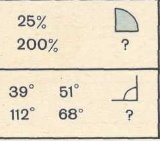
стаття "Задачі на відсотки"

Бас В. М., Бас С. В., Блинов В.

м. Кривий Ріг

 

ОСОБЛИВОСТІ ВИКЛАДАННЯ ТЕМИ «ВІДСОТКИ» У ШКІЛЬНОМУ КУРСІ МАТЕМАТИКИ

 

Тему «Відсоткові розрахунки» в шкільному курсі математики і вчителі, і учні вважають одною з найскладніших тем. І це зовсім необґрунтовано. Вся складність цієї теми полягає в тому, що її викладають не системно і не враховуючи зв’язки між різними розділами математики. Тому є необхідність систематизувати навчальний матеріал з теми «Відсотки» таким чином, щоб учні могли легко засвоїти його та застосувати у житті. Для досягнення цієї мети необхідне виконання наступних умов:

1. Розуміння теми з боку учня (тому один з співавторів учень).

2. Розробити методику викладання теми вчителеві (один з співавторів вчитель школи).

3. Наочно пов’язати вивчене у школі з тим, що чекає в ВНЗ (третій співавтор викладач ВНЗ).

Перед викладанням теми «Відсоткові розрахунки», обов’язково треба повідомити деякі історичні факти, але не слід дуже заглиблюватись в історію (особливо, коли розповідаєш учням молодших класів). Ми вважаємо, що матеріалу, наведеного нижче, буде цілком достатньо.

Термін «procento» спочатку зображували повністю, в рукописах писали його часто скорочено — «сто». Це скорочення поступово перетворилося на знак який поряд з повним написанням назви відсотка, вперше зустрічається в друкованому виданні комерційної арифметики de la Porte'a (Париж, 1685). Поступово завойовуючи собі місце, цей знак особливо часто став з'являтися в друкованих виданнях на початку XIX ст. Широке поширення знаку «%» у друкованих виданнях призвело до того, що вже в середині XIX ст. він отримав загальне визнання, як символ відсотка. Відсотки з комерційної практики поступово проникли в різні галузі техніки і знання. Область застосування відсотків швидко розширилася, охоплюючи різні науки.

Після цього можна приступити до подання фактичного матеріалу теми. Тему «Відсотки» починають вивчати у п’ятому класі. Існує досить багато різноманітних методик для вивчення цієї теми. Ми, порадившись з нашим співавтором (учнем) вибрали, як нам здається, найбільш ефективну.

1 частина.

Учням п'ятого класу тему «Відсотки», а саме розділ «Знаходження відсотку від числа» доцільно пояснити на прикладі задачі:  «В 100 ящиках 450 кг яблук. За тиждень продали 26 ящиків. Скільки продали кг яблук?». Такі задачі більшість учнів в 5 класі вже вміють розв’язувати. Тому розв’язавши її можна перейти до відсотків, а саме:

Площа поля 450 га. За тиждень зібрали врожай з площі, що становить 26% поля. З якої площі (в гектарах) було зібрано врожай?

Розв'язання:

 Уявимо квадрат розміром 10 на 10 клітинок. Усього у квадраті 100 клітинок. Кожну клітинку можна прирівняти до одного відсотка. Виходячи з умови: нам треба розмістити 450 га поля на 100 клітинок. Тобто поділити площу нашого поля на 100%:

450 га / 100% = 4,5 га.

Тепер ми можемо сказати, що один відсоток або одна клітинка у нашій схемі дорівнює 4,5 га.

Звідси можна знайти 26% від усієї площі поля, тобто з якої площі зібрали врожай за тиждень. Для цього нам потрібно дізнатися скільком гектарам буде дорівнювати 26 клітинок. Ми помножимо 26% ( за тиждень зібрали з площі ) на 4,5 га. (значення одного відсотка):

4,5га. * 26%(клітинок) = 117 га.

Отже, 117 га – за тиждень зібрали з площі (26% від площі усього поля).

На схемі це можна показати так:

 

 

Де синій колір - за тиждень зібрали з площі (26% від площі всього поля або 117 га).

Зелений колір – решта площі поля (100% - 26% = 74% або 74 клітинки).

Для самостійного розв’язання варто запропонувати наступні завдання:

1. Площа лісу 150 га. За перший день бригада лісорубів вирубала 16% лісу. Скільки лісу (в гектарах) вирубали лісоруби за перший день?

2. Площа аеродрому 460 га. За перший місяць бригада робітників вдосконалила 18% площі всього аеродрому. Яку площу (в гектарах) вдосконалила бригада за перший місяць?

3. Об'єм  води у резервуарі 850 л. За один день звідти випарувалось 12% води. Скільки води (у літрах) випарувалось за один день?

Дуже корисними в цьому випадку виявляться задачі на розчини та сплави. Це життєві задачі (кулінарія, консервація) та задачі, що орієнтують учнів на вибір майбутньої професії та розвивають міжпредметні зв’язки. На цьому потрібно акцентувати як можна більше уваги, щоб в учнів не виникало питання «А де нам це знадобиться?»

4. Сплав бронзи і алюмінію містить 64% бронзи. Скільки тон бронзи міститься в 800 т такого сплаву?

5. Розчин містить 7% солі. Скільки кілограм солі міститься у 400 кілограмах такого розчину?

6. Мінеральна вода містить 5% мінеральних речовин. Скільки грам мінеральних речовин містить 600 г такої води?

Але можна придумати і такі задачі, що є актуальними сьогодні. Колега з Тернівської школи №7 Сидорова О.П. у своїй роботі «Використання задач прикладного змісту при вивченні математики в основній школі» запропонувала наступні задачі:

7. Кімната обладнана приладами освітлення, які споживають 300 Вт . Якщо замінити їх на енергозберігаючі прилади, то витрати скоротяться на 30%. Скільки ват протягом доби можна заощадити, використовуючи енергозберігаючі прилади?

8. Одна кіловат-година електроенергії коштує 0,36 грн. Якщо кожен із 4 членів сім’ї збереже 10% електроенергії за умови, що протягом місяцю сім’я споживає 150 кВт, то скільки гривень буде заощаджено за місяць?

9. Сім’я з трьох чоловік у жовтні витратила 150 кВт електроенергії,  а в листопаді на 20% більше. Якщо 1 кВт коштує 0,36 грн., то на скільки відсотків більше заплатили у листопаді, ніж у жовтні?

10. У будинку 10 дерев’яних вікон. Заміна 1 вікна збереже 2% тепла. За місяць родина платить 300 гривень за теплопостачання . На скільки скоротиться плата родини в разі заміни всіх вікон?

11. Під час приготування їжі на одній конфорці за 1 день витрачається 0,012м³ газу при інтенсивному вогні. Якщо тиск газу зробити помірним, то економія буде 30%. Один м³ газу коштує 0,73 грн. Якою буде економія сімейного бюджету через місяць?

Якщо ж пошукати в Інтернеті, то можна знайдти ще багато цікавих і корисних задач. Проте слід не забувати наголошувати учням, в яких галузях ці задачі розв’язуються ( медицина,промисловість та ін.).

12.  Цукровий буряк накопичує 25% цукру, тоді як цукрова тростина – лише 18%. Скільки тонн цукрової тростини треба переробити, щоб отримати стільки ж цукру, як із 3600 т цукрових буряків?

13.  Щоб замісити пісочне тісто треба брати маргарину 70% від маси борошна. Скільки треба взяти маргарину, якщо борошна 400 г?

14. На ярлику светра написано: Склад – 60% поліамід, 40% - ангора. Скільки пішло на светр ниток ангори, якщо маса светра 900 г?

15. Ганна Іванівна взяла у банку кредит у сумі 2000 грн. під 16% річних. Визначте, яку суму повинна сплатити вона банку через рік?

16. Через легені проходить щодоби 1200 л повітря. Кров, що проходить через легені становить 50% від об’єму повітря. Скільки літрів крові проходить щодоби через легені?

 

Аналогічно можна пояснити тему «Знаходження числа за значенням його відсотків». Пропонуємо учням для розв’язання наступну задачу.

За перший тиждень автобус з туристами подолав відстань 4000 км, що склало 80% від повної довжини маршруту екскурсії. Яка довжина повного маршруту?

Розв'язання.

Уявимо квадрат розміром 10 на 10 клітинок. Усього у квадраті 100 клітинок. Кожну клітинку можна прирівняти до одного відсотка. Виходячи з умови, нам треба розмістити 4000 км порівну на 80 клітинок(%). Так як 4000 км це 80%, то ми знайдемо скільки кілометрів припадає на один відсоток. Тобто треба поділити 4000 км на 80%:

4000 км / 80% = 50 км.

Тепер ми можемо сказати, що один відсоток або одна клітинка у нашій схемі дорівнює 50 км.

Звідси можна знайти повну довжину маршруту (100%), помноживши значення одного відсотка на 100%:

50 км (1%) * 100% = 5000 - довжина повного маршруту.

На схемі це можна показати так:

 

 

Кожна клітинка дорівнює одному відсотку (50 км);

Сірий колір – 80 клітинок (80%) від усього маршруту (4000 км);

Зелений колір – 100% - 80% = 20% (решта маршруту).

Для самостійного розв’язання:

1. За місяць турист подолав відстань 700 км, що склало 70% від запланованої їм відстанні. Скільки кілометрів планував подолати турист?

2. Катер проплив за 2 годин 30 км, що склало 15% від його денного маршруту. Яка довжина його повного денного маршруту?

3. Літак за годину пролетів 400 км, що склало 28% від повного маршруту. Скільки повинен пролетіти літак?

4.  Сплав алюмінію і олова містить 35% олова. Скільки треба узяти такого сплаву, щоб у ньому було 70 кг олова?

5. Розчин містить 10% солі. Скільки треба узяти такого розчину, щоб після повного випарування води залишилось 120 кг солі?

6. Напій містить 5% цукру і інших домішок. Скільки треба узяти такого напою, щоб після повного випарування води залишилось 100 г сухої речовини?

7. Доктор Айболіт зі своїми друзями плив на кораблі по річці Лімпопо, щоб вилікувати хворих звірів. Коли вони пропливли 60% шляху, на них напали пірати. Але друзі перехитрили піратів, і 80км шляху, що залишилися, пропливли на піратському кораблі. Скільки кілометрів складає весь шлях доктора Айболіта?

8. Щоб утворився 9% оцет, кухар взяв 22,5 мл оцтової кислоти. Скільки він отримав 9% оцту?

9. Для виготовлення новорічного костюма шахової королеви використовували чорну та білу тканину. Білої пішло 1,2 м, що становить 48% від усієї використаної тканини. Скільки всього пішло тканини на костюм?

10. Ощадний банк сплачує своїм вкладникам 12 % річних. Скільки грошей треба покласти в банк, щоб через рік одержати прибуток 54 грн.?

11. Для зміцнення здоров’я та покращення дихання лікарі радять проходити в день 3 кілометри на свіжому повітрі. Це становить 0,1% довжини повітряних шляхів, що містять легені людини. Яка довжина дихальних шляхів?

 

І останнє, що ми розглядаємо в 5 класі – «Відсоткове відношення». Тут учні дуже часто плутають «що на що ділити». І знову на допомогу приходить малюнок.

У класі 30 учнів. Хлопців – 12. Який відсоток хлопців в класі?

Розв’язання.

Вчителю треба обов’язково наголосити, що спочатку встановлюємо  величину відповідну 100% (Це дуже знадобиться в 6 класі при розгляді теми «Пропорції»).  

 

Знов, говоримо про те, що 30 учнів відповідає 100 клітинкам. Тому перша дія: 30:100=0,3 учня відповідає одному відсотку. Тоді другою дією знаходимо скільком кліткам-відсоткам відповідає 12 учнів: 12:0,3=40. Отже, хлопців в класі 40%.

Зазначимо, що задачі на відсоткове відношення у реальному житті зустрічаються частіше, ніж попередні: це економіка(прибутки, падіння та зростання ВВП), промисловість (зростання попиту, якість продукції) та обов’язково соціологія (вибори, соц. опитування).

Для самостійного розв’язання пропонуємо наступні завдання:

1. На виборчій дільниці № 85 с. Комишуваха 2060 виборців. На виборах проголосувало 927 виборців. Який відсоток виборців прийняли участь у виборах?

2. Цього літа фермер зібрав 450 т пшениці, 180 т він видав на паї людям. Який відсоток пшениці залишилося у фермера після цього?

3. Визначте відсоток вмісту цукру в сиропі, якщо 250 г сиропу містить 115 г цукру. (презентувати на дошці)

4. На пошив одного смокінгу потрібно 2,5 м тканини. В рулоні 50 м тканини. Який відсоток тканини іде на пошив смокінга?

5. Ціна мультиварки зросла з 1400 грн. до 1750 грн. На скільки відсотків підвищилася ціна?

6. Із 49 млн. українців курять 19 млн. Який це відсоток?

Але сформувати навички розв’язування простих задач недостатньо для того, щоб у учня сформувалась база з даної теми. Необхідно розв’язати і більш складні задачі, в яких застосовувались або один спосіб декілька разів, або декілька способів.

1. Автобус подолав 580 км до Одеси, щоб туристи змогли відпочити на Чорному морі. В дорозі було всього дві зупинки. За перші дві години автобус пройшов 30% шляху, за другі дві години – 35% шляху. Скільки кілометрів залишилося пройти?

2. Периметр рівнобедреного трикутника дорівнює 140 см. Знайти його сторони, якщо основа трикутника на 20% менше, ніж бічна сторона.

3. Перше число рівне 160, друге складає 40 % від першого, третє – 70 % від другого. Обчислити середнє арифметичне цих чисел.

4. Костюм коштував 600 гривень. Спочатку його ціну зменшили на 20%, а згодом підвищили на 25%. Як змінилась ціна костюма?

5. Спортивні змагання тривали три дні. Першого дня в них взяли участь 34% усіх учасників, другого дня – 30%, а третього – решта 135 осіб. Скільки всього було учасників змагань?

6. В одній школі дівчатка становлять 25% всіх учнів, відомо, що хлопчиків у цій школі на 26 менше, ніж дівчаток. Скільки всього учнів навчається в школі?

7. Три вантажівки перевезли деякий вантаж. Перша вантажівка перевезла 40% всього вантажу, друга 25% того, що залишилось, а третя – решту 9 т. Скільки тонн вантажу було перевезено трьома вантажівками разом?

І бажано все це закріпити логічними вправами та олімпіадними задачами. Задачі на логіку ми позичили з чудової книги А.Г.Гайшута «Математика в логічних вправах»:

1.                                                   2                                                          3. .                           

 

 

 

 

4.                                                       5.

 

 

6.

 

 

1.                  

 

 

 

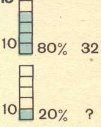
А олімпіадні задачі ми пошукали в олімпіадах для молодших класів різних рівнів.

1.               Зібрали 100 кг грибів. Як виявилось, їх  вологість 99 %. Коли  гриби висушили, вологість знизилась до 98 %. Якою  стала маса цих  грибів після сушіння?
2.            Частина мешканців одного міста вміє розмовляти тільки російською, частина – тільки українською і частина вміє розмовляти обома мовами. Українською говорять 85 % мешканців, а російською – 75 %. Скільки відсотків мешканців говорять обома  мовами?
3.            Бригада косарів в перший день скосила половину поля та ще 2 га, а в другий день – 25 % частини, що залишилась  і останні 6 га. Знайти площу поля. (20 га)
4.            З учнів, що виконували контрольну роботу, 30 % получили «5», 40 % - «4», 8 учнів – «3», останні – «2». Середній бал виявився рівним 3,9. Скільки учнів отримали кожну  з оцінок? (12, 16, 8, 4)
5.            В трьох класах виконувалась контрольна робота. Отримали  «5» - 28 учня, «4»  - 35, «3» - 29, «2» - 8 % учня. Скільки учнів получили оцінку «2»? (8)
6.            Одного разу грибів я зібрав! – ледве доніс. Але ніс майже одну воду – в свіжих грибах її 90%. А коли  гриби висушили, вони стали на 15 кг легше. Тепер в них було 60% води. Скільки грибів я приніс з лісу?

 

 

2 частина.

Продовжують вивчати тему «Відсотки» в шостому класі. Хоча окремого розділу в програмі нема, її ми зустрічаємо і при вивчені теми «Звичайні дроби», і при вивчені теми «Відношення та пропорції». Деякі вчителі не приділяють увагу задачам, що містять відсотки, тому учні розв’язують їх, використовуючи знання п’ятого класу. Це є великою помилкою. Але давайте поступово.

Коли учні вивчили всі дії зі звичайними добами, треба обов’язково навчити їх розв’язувати задачі на відсотки, використовуючи саме перехід  від відсотків до дробів. По-перше, це покаже зв’язок між темами «Відсотки» та «Знаходження дробу від числа», «Знаходження числа за значенням його дробу». По-друге, в темі «Розв’язування задач на складання рівнянь» прискорить  розуміння учнів при розв’язуванні задач на відсотки.  

Навчити переводити відсотки у дріб дуже легко. Нам тут допоможе сам термін «відсотки». Акцентуючи увагу, що відсоток – це «від СОТОК», легко переводимо відсотки у десятковий дріб. А від десяткового дробу, після недавно вивченого, переходимо і до звичайного дробу.

Учням шостого класу знаходження відсотку від числа можна пояснити на прикладі задачі:

  Площа поля дорівнює 750 га. На 36% усієї площі росте картопля. Скільки гектарів поля займає картопля?

Задачу можна розв’язати  методом п'ятого класу. Тобто, поділити число на 100% і помножити на відсоток, значення якого нам треба знайти:

750 га / 100% * 36% = 270 га.

Уявимо квадрат розміром  10 на 10 клітинок. Усього у квадраті 100 клітинок. Кожну клітинку можна прирівняти до одного відсотка.  Виходячи з умови: нам треба розмістити 750 га порівну на 100 клітинок(%). Так як 750 га це 100%, то ми знайдемо скільки гектарів припадає на один відсоток. Тобто треба поділити 750 га на 100%:

На схемі це можна показати так:

 

 

Кожна клітинка дорівнює одному відсотку (7,5 га);

Сірий колір – 36 клітинок (36%) від площі поля (площа на якій росте картопля);

Зелений колір – 100% - 36% = 64% (решта поля).

Але враховуючи вище зазначене, розв’яжемо задачу іншим способом.  Для того щоб виразити 36% від 750 га.  можна просто помножити 750 га на відсоток (значення якого нам треба знайти) поділений на 100(%), у нашому випадку це буде (якщо записати десятковим дробом це буде 0,36). Виконаємо дію:

750 га * 0,36 = 270 га.

Відповідь: 270 га займає картопля.

Завдання для самостійного розв’язання:

1. Площа поля 240 га. За день зорали 15% поля. Скільки гектарів площі поля зорали за день?

2. Довжина дороги 3500 км. За тиждень відремонтували та вдосконалили 12% дороги. Скільки кілометрів дороги відремонтували та вдосконалили за тиждень? 

3.На полиці у міській бібліотеці стоїть 250 книжок. Книги зарубіжних письменників складають 36% від 250. Скільки книжок зарубіжних письменників стоїть на цій полиці?

4. На полі посаджено овочі. Площа, яку займає картопля становить 30% від усього поля, морква – 110% картоплі, цибуля — моркви, а решта – капуста. Яку площу займає капуста? (площа поля дорівнює 300 га).  

5. На купівлю, телевізора, мікрохвильовки, комп’ютера та холодильника витратили 75000 грн. Телевізор коштував від усіх витрачених грошей, мікрохвильовка – 21% решти, комп’ютер – в 2 рази більше ніж мікрохвильовка. Скільки коштував холодильник?

 

До речі, можна використовувати задачі, які ми наводили для п’ятого класу.

Аналогічно покажемо приклад і для теми «Знаходження числа за його відсотком».

За перший день зорали 36 га, що становило 12% від усього поля. Яка площа поля?

Відповідь можна знайти методом п’ятого класу. Тобто поділити число на відсоток, який воно становить і помножити на 100%:

36 га ÷ 12% * 100% = 300 га.

Уявімо квадрат розміром  10 на 10 клітинок. Усього у квадраті 100 клітинок. Кожну клітинку можна прирівняти до одного відсотка.  Виходячи з умови: нам треба розмістити 36 га порівну на 12 клітинок(%). Так як 36 га це 12%, то ми знайдемо скільки гектарів припадає на один відсоток. Тобто треба поділити 36 га на 12%:

На схемі це можна показати так:

 

 

Кожна клітинка дорівнює одному відсотку (3 га);

Сірий колір – 12 клітинок (12%) від площі поля (36 га);

Помаранчевий колір – 100% - 12% = 88% (решта поля).

Але у шостому класі це можна записати трохи інакше. Для того щоб знайти площу поля (100%). Можна просто поділити 36 га на 12%, які ми перевели у дріб 0,12(або ).

Виконаємо дію:

36 га ÷=300

Відповідь: 300 га площа поля.

Малюнки тут використовувати теж доречно, бо учні часто не розуміють «коли множити, коли ділити». А за малюнками розуміння теми приходить скоріше.

Задачі для самостійного розв’язання:

1.За перший тиждень автобус проїхав 1560 км, що склало 75% від усього маршруту. Яка довжина повного маршруту?

2. Авансом робітник одержав 3200 грн., що становить 40% від його заробітної плати. Яка зарплата у робітника? 

3. На купівлю яблук витратили 49 грн., що склало 7% від витрачених грошей. Скільки усього грошей витратили?

4.  За тиждень поля зібрали врожай масою 9450 кг, що склало 105% від плану. Скільки планували зібрати врожаю?

5. Купили моркву, картоплю і цибулю. На моркву витратили 35%, на картоплю – 45%, а на цибулю – решту, що склало 40 грн. Скільки усього грошей витратили на купівлю овочів?

6. Розчин містить 30% солі, цукру – 40%, інших речовин – решту, що складає 90 г. Яка маса усього розчину?

Наступна тема, де ми зустрічаємось з відсотками – «Відношення та пропорції». Тема дуже важлива (вона буде корисна і при вивченні хімії, і при вивченні фізики), але також  є серйозною проблемою в подальшому вивченні відсотків. Справа в тому, що пропорція полегшує розв’язання задач на відсотки (особливо при знаходженні відсоткового відношення), а це приводить до того, що учні нехтують раніш вивченим (розв’язувати задачі, переводячи відсоток до дробу). Тому вчителеві треба бути наполегливим і не дати забувати учням вивчене раніше. Ми ж зупинимось саме на знаходженні відсоткового відношення через пропорцію. Тому що, як ми вже зазначали, в учнів це викликає проблему. Наведемо як приклад задачу, в якій більшість учнів роблять помилку.

 Огірки коштували 20 грн. за 1 кг. Через місяць їх ціна змінилась на 60%. Ще через місяць ціна знову стала 20 грн. На скільки відсотків піднялась ціна за останній місяць?

 Перш ніж розв’язувати задачу, треба учням пояснити і економічні моменти знецінення та підвищення ціни огірків (пояснити такі поняття як «сезон» і «не сезон»).

Складність  самої задачі полягає в тому, що учні не розуміють до кінця поняття « 100 %». Вони як позначили першу ціну за 100%, так вона і залишається константою поки задачу не розв’яжуть. Тому їх відповідь для багатьох вчителів передбачувана – 20%. Але поняття «100%» - це поняття відносне. І вчитель, якщо хоче виховати компетентну людину, повинен це показати. Отже, нехай початкова ціна 20 грн. – 100%, тоді нову ціну (60%) позначимо через х. Складаємо пропорцію та розв’язуємо її.

100÷20=60÷х;

х=12.

Таким чином нова ціна огірків – 12 грн. І тепер ця ціна буде 100%! Треба знайти відсоткове відношення 20 грн. до 12 грн. Позначаємо 20 грн. як х%, і складаємо пропорцію:

 100÷12=х÷20.

Звідси 20 грн. приблизно 167%, а отже ціна піднялась на 67%.

Однієї задачі для учня недостатньо, щоб зрозуміти зміст відсотків, тому вчитель повинен сам скласти задачі, добираючи їх з життя. Пропонуємо задачі, які використовували ми.

1.     Поруч стоять 2 магазина. Кожен магазин на одне і теж взуття, яке коштувало 1500 грн. зробив знижки. Перший зробив знижки двічі: на 20%, а потім на 30%. А другий відразу на 50%. Де вигідніше купувати?
2.     Ви поклали 20000 на дивіденди в банк під 20% річних. Порівняйте виплати через рік, два роки, три роки?

Але зустрічаються задачі де взагалі немає початкової величини, і учневі треба знайти невідоме у відсотках. Учні лякаються таких задач, а вчителі їх обходять стороною.  І ось тут знадобляться знання, переводу відсотків у дріб. Розглянемо розповсюджену задачу:

 

 Ціна деякого товару спочатку підвищилась на 20%, а потім знизилась на 20%. Як змінилась ціна товару і на скільки?

 

Якщо учні зрозуміли попередній етап, то вони вам скажуть, що ціна змінилася. Деякі, увівши свою ціну, скажуть як вона змінилася. Але це буде частковий випадок, а не загальний розв’язок. Необхідно скласти алгоритм знаходження відповіді і кінцеву формулу (Акцентуйте увагу на том, що так і працюють програмісти. Це зацікавить деяких учнів).

Отже, нехай початкова ціна х. Тоді при зменшенні ціни на 20% (тобто вона складає 80%), нова ціна буде – 0,8х. Тепер відштовхуючись від нової ціни (вона знов 100%), підвищуємо її на 20%, і вона стає 120%. Тоді остаточна ціна – 1,2∙0,8х=0,96х. порівнявши початкову ціну х і остаточну ціну 0,96х бачимо, що остання менша на 4% (1-0,96=0,04).

Задачі для самостійного розв’язання:

1.     За перший рік підприємство збільшило випуск продукції на 8%, в наступному році випуск збільшився на 25%. На скільки відсотків зріс випуск продукції в порівнянні з первинною?
2.     Внаслідок інфляції ціни зросли на 150%. Рада зажадала від уряду повернення цін до попереднього рівня. Для цього ціни повинні бути зменшені (на скільки відсотків)?
3.     Ціну товару спочатку знизили на 20%, потім нову ціну знизили ще на 15% і, нарешті, після перерахунку, знизили ще на 10%. На скільки процентів всього знизили початкову ціну товару?
4.     У січні завод виконав 105% місячного плану випуску готової продукції, а в лютому дав продукції на 4% більше, ніж у січні. На скільки відсотків завод перевиконав двомісячний план випуску продукції?
5.     До магазину завезли огірки, кабачки і перець.  Маса огірків становить 20% маси кабачків, а маса кабачків становить 25% маси перцю. У скільки разів маса перцю більша за масу огірків?

 

Попередні  задачі стануть у нагоді при розв’язуванні задач на складання рівнянь.  Учневі буде тепер не важко зрозуміти, як саме скласти рівняння, використовуючи відсотки. Розглянемо на прикладі.

  За зміну 3 робітники виготовили партію деталей. Перший робітник виготовив 22 деталі, другий – 30% усіх деталей, а третій – на 2 деталі більше, ніж другий. Скільки всього деталей виготовили робітники?

Розв’язання:

Приймемо за Х те, що запитується в задачі, - кількість деталей всього. Тоді другий виготовив 0,3Х, а третій – 0,3Х+2. Оскільки всі разом виконали Х деталей, то маємо

   22+0,3Х+0,3х+2=Х.

Розв’язуючи рівняння маємо, що кількість всіх деталей 60.

Ще одна цікава задача, яку ми покажемо, безпосередньо відноситься до попередньої  теми.

 

Дід Макар вирішив продати своїх телят.  У перший тиждень їх ніхто не купив, і довелося знизити ціну на 25%. Через тиждень Макар знизив ціну ще на 20%, і тільки тоді телят купив дід Грицько за 720 грн. Якою була початкова ціна?

Розв’язання:

Приймемо початкову ціну за Х. Тоді після першого тижня вона становила 0,25Х. А після другого – 0,2∙0,25Х, або 0,5Х. Маємо рівняння:

  0,5Х=720.

Звідси Х=1440. І початкова ціна телят 1440 грн.

 

Задачі для самостійного розв’язання:

1.     Двоє робітників виготовили разом 86 деталей. Перший виготовив на 15% деталей більше, ніж другий. Скільки деталей виготовив кожен робітник?
2.     У трьох цехах заводу працює 101 робітник. Кількість робітників першого цеху становить кількості робітників третього цеху, а кількість робітників другого цеху – 80 % кількості робітників третього. Скільки робітників працює у першому цеху?
3.     На трьох полицях стояли книжки. На першій полиці стояло 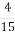усіх книжок, на другій – 60% усіх книжок, а на третій на 8 книжок менше, ніж на першій. Скільки всього книжок стояло на трьох полицях?
4.     У чотири бідони розлили молоко. У першій бідон налили 30% усього молока, у другий - того, що в перший, у третій – на 26 л менше, ніж у перший, а в четвертий – на 10 л більше, ніж у другий. Скільки літрів молока розлили в чотири бідони?
5.     Однакові деталі  обробляють на двох верстатах. Продуктивність  першого верстата на 40% більший за продуктивність другого. Скільки деталей було оброблено за зміну на кожному верстаті, якщо  перший працював у цю зміну 6 годин, а другий 8 годин, причому на обох верстатах разом було оброблено 820 деталей?

Наступні задачі можна розв’язувати як за допомогою рівнянь, так і за допомогою систем рівнянь,  які учні  вивчать в сьомому класі.

6.          Вкладник поклав у банк 300 грн. на два різних депозитних рахунки, причому за першим рахунком йому нараховували 7% річних, а за другим - 8% річних.  Через рік він одержав 222 грн. прибутку. Яку суму було внесено на кожний рахунок?
7.          Маємо два сплави міді й цинку. Перший сплав містить 9% цинку, а другий – 30%. Скільки кілограмів кожного сплаву треба взяти , щоб отримати сплав масою 300кг, який містить 23% цинку.
8.          Маємо два водно-сольових розчини. Перший розчин містить 25% солі, а другий – 40%. Скільки кілограмів кожного розчину треба взяти, щоб отримати розчин масою 50 кг, який містить 34% солі?
9.          У першому бідоні було молоко з масовою часткою жиру 2%, а в другому – 5%. Скільки треба взяти молока з кожного бідона, щоб отримати 12 кг молока, масова частка жиру якого дорівнює 4 %?

І знов пропонуємо  задачі на логіку та задачі з олімпіад різних рівнів.

1.  

 

 

2.                                                                                 3.

 

 

 

4.

 

 

 

5.          Вчора кількість учнів , присутніх  в класі, було в вісім разів більше за відсутніх. Сьогодні  не прийшло ще два учня, і виявилось, що відсутні складають 20 % від числа учнів, присутніх в класі. Скільки всього в класі учнів?
6.          До задуманого натурального числа дописали праворуч цифру 7 і від утвореного нового числа відняли квадрат задуманого числа. Після цього отриману різницю зменшили на 755, а потім від результату відняли задумане число. У підсумку отримали число 0. Знайдіть число, яке було задумано спочатку.
7.          Маємо три сплави. Перший сплав містить 30% олова і 70% міді, другий – 10% міді і 90% свинцю, а третій – 15% олова, 25% міді і 60% свинцю. З цих трьох  сплавів приготували новий сплав, що містить 40% свинцю. Знайдіть найбільший і найменший вміст міді, який може бути в новому сплаві.
8.          На підприємстві випускалось 98% продукції на рівні світових стандартів. Завдяки впровадженню сучасної електроніки підприємство стало випускати вже 99,5% такої продукції. На скільки відсотків зменшився випуск продукції якості нижчою за світові стандарти?
9.          Як зміниться величина дробу, якщо чисельник збільшити на 200%, а знаменник зменшити на 50%?
10.     Знайти двозначне число, яке від суми цифр цього числа складає 500%.
11.     Обчислити раціональним способом :

3,84% від 25;      37,5% від 39120.

 

3 частина.

 

До третьої  частини ми відносимо задачі які розглядаються в сьомому та восьмому класах, оскільки нічого нового за ці два роки про відсотки учні не вивчають. Та на превеликий жаль, вчителі теж обходять відсотки стороною. Тому деякі учні згадують про відсотки лише в 9 класі, де є тема  ”Відсоткові розрахунки ”, а це дуже великий проміжок, щоб забути раніш вивчене. Тому як в 7, так і в 8 класах ми наполегливо рекомендуємо розв'язувати задачі на відсотки.

Наприклад, в 7 класі при вивченні теми “Розв’язування задач на складання систем рівнянь ” треба розглянути деякі задачі, які потім зустрічаються на ДПА або ЗНО. Частину задач ми вже презентували раніше в 6 класі. Давайте розглянемо одну з них.

Скільки кілограмів 25-відсоткового і скільки кілограмів 50-відсоткового сплавів міді треба взяти, щоб отримати 20 кг 40-відсоткового сплаву?

Розв’язання.

Розглянемо обидва випадки: через рівняння та через систему рівнянь.

Випадок 1.

Нехай першого сплаву взяли Х кг. Тоді другого – 20-Х кг. Знайдемо кількість міді в кожному сплаві та в отриманому. Перший сплав містить міді 0,25Х кг, другий сплав містить – 0,5(20-Х) кг міді і загальний сплав – 0,4·20 кг міді. Отже, можна скласти рівняння.

  0,25Х+0,5(20-Х)=8.

Звідси Х=8. Отже, першого сплаву треба взяти 8 кг, а другого – 12 кг.

Випадок 2.

Нехай першого сплаву взяли Х кг, а другого – У кг. Оскільки в результаті отримали 20 кг, маємо перше рівняння: Х+У=20. Як і в попередній задачі, знайдемо масу міді в кожному сплаві. В першому – 0,25Х, в другому – 0,5У, в загальному – 0,4·20. Маємо друге рівняння: 0,25Х+0,5У=8. Звідси складаємо систему рівнянь:

  

В результаті маємо таку ж відповідь: 8 кг та 12 кг.

Учень обов`яково повинен вміти користуватися обома способами. Але якщо в задачах такого типу системою можна знехтувати, то наступні задачі простіше розв`язувати саме через системи.

1.          За 2 футбольні і 4 волейбольні м`ячі заплатили 1000 грн. після того як футбольний м`яч подешевшав на 20%, а волейбольний подорожчав на 10%, то за один футбольний і один волейбольний м`ячі заплатили 325 грн. Якою була початкова ціна кожного м`яча?
2.          Відомо, що за 4 кг огірків і 3 кг помідорів коштували 34 грн. після того як огірки подорожчали на 50%, а помідори подешевшали на 20%, за 2 кг огірків і 5 кг помідорів заплатили 36 грн. знайдіть початкову вартість 1 кг огірків і 1 кг помідорів.
3.          З одного поля зібрали по 40 ц ячменю з гектара, а з другого – по 35 ц з гектара. Усього було зібрано 2600 ц. Наступного року урожайність першого поля збільшилась на 10%, а другого – на 20%, а весь зібраний врожай збільшився на 400 ц. Знайдіть площу кожного поля.
4.          Вкладник поклав у банк гроші на два різних рахунки, по одному з яких нараховували 5% річних, а по другому – 4%, і отримав через рік за двома вкладами 1160 грн. прибутку. Якби внесені на різні рахунки кошти поміняли місцями, то річний прибуток становив би 1180 грн. Скільки  всього грошей вніс до банку вкладник?

Задачі підвищеної складнощі та олімпіадні задачі:

1.               До книгарні для продажу надійшли підручники з фізики та математики. Коли було продано 50% підручників з математики і 20% підручників з фізики, що становить у сумі 390 книжок, то підручників з математики залишилось у три рази більше, ніж підручників з фізики. Скільки підручників з математики і скільки підручників з фізики надійшло у продаж?
2.               Музичний театр оголосив конкурс на вступ до оркестру. Спочатку планувалось, що число місць для скрипалів, віолончелістів і сурмачів розподілиться у відношенні 1,6:1:0,4. Проте потім було вирішено збільшити прийом, і в результаті скрипалів було прийнято на 25% більше, а віолончелістів на 20% менше, ніж передбачалось. Скільки музикантів кожної спеціальності було прийнято до оркестру, якщо всього прийняли 32 особи?
3.               Кристал, який знаходиться у стані формування, рівномірно нарощує свою вагу. Спостерігаючи формування двох кристалів, помітили, що за рік перший кристал збільшив свою початкову масу на 4%, а другий -  на 5%, в той час як приріст маси першого кристала за 3 місяці виявився рівним приросту маси другого кристала за 4 місяці. Які були початкові маси цих кристалів, коли відомо, що після того, як кожна з них збільшилась на 20 г, відношення маси першого кристала до маси другого кристала становило 1,5?
4.               На яке ціле додатне число треба поділити 180, щоб остача становила 25% від частки?
5.               Наша школа взяла участь у волейбольному чемпіонаті міста, який продовжувався цілий рік. Команд було 6, кожна зіграла по чотири ігри з кожною з решти команд.  Відомо, що решта команд мають відповідно 80% перемог (від своєї загальної кількості ігор), 60%, 55%, 40% та 35%. Про свої здобутки ми скромно мовчимо, але ви можете їх визначити. Нічиїх у волейболі не буває.
6.               Випускниця університету працює нянею в трьох родинах, куди її влаштувало агентство. Вона повинна віддавати агентству 20% з перших 100 доларів, зароблених за місяць, 15% з кожного долара між сто першим і двохсотим та 10% з кожного долара, починаючи з двохсот першого. Якщо всього агентство заробило на ній 42 долари за останній місяць, скільки залишилось з зароблених грошей їй?
7.               В стайні було 8 коней та 15 корів. Щоденно худоби з цієї стайні виділяли по 162 кг сіна. На скільки відсотків кожен кінь одержував щоденно більше сіна ніж кожна корова, якщо 5 коней одержували на 3 кг сіна більше, ніж 7 корів?
8.               40% мишей, над якими проводили дослід, були чоловічої статі. Частина мишей померла, з них 25% були чоловічої статі. Визначить, в скільки разів смертність серед мишей жіночої статі перевищила смертність серед чоловічої?
9.               Визначить, який прибуток від продажу закупленого товару розраховував одержати продавець, якщо він сподівався уникнути податку 20% з  продажу, але це йому не вдалося, і все одно прибуток склав 60%.

 

Що стосується восьмого класу, то в підручниках ви взагалі не знайдете задач з відсотками. А якщо вони і будуть, то лише одна-дві (і то під зірочками). А в цьому класі вивчаються такі теми, як  ”Задачі на складання квадратних рівнянь ”,  ”Задачі на складання раціональних рівнянь ”, де треба розглянути задачі з відсотками. Наведемо приклади різних  задач, які можна запропонувати учням в восьмому класі .

1. За 3,5 год. роботи один штампувальний прес може виготовити 42% усіх замовлених деталей. Другий за 9 год. роботи може виконати 60% усіх деталей, а швидкості виконання роботи на третьому і другому пресах відносяться як 6:5. За який час буде виконано все замовлення, якщо всі три преси працюватимуть одночасно?
2. Хацапетівка стала містом, і в ній обирають мера. Кандидат Юнко набрав рівно 51% голосів. Кандидат Янко – 49% голосів. При цьому вони обидва не брали участі у голосуванні. Скільки би набрав Юнко, якби кожен з них проголосував?
3. Чому дорівнює відсоткове відношення середньо арифметичного двох чисел до їх середнього геометричного, якщо одне число в чотири рази більше іншого?
4. Очищувальна  споруда наповнюється забрудненою водою, що містить 10% шкідливих речовин. Через деякий час після спуску очищувальної води, концентрація шкідливих речовин в тій масі, що залишилась, складає вже 20%, а загальна маса всієї рідини зменшилась на 600 кг. Кожен такий цикл вимагає затрат в 1000 доларів. Чи окупляться затрати, якщо власник фільтру виділить 1500% цієї суми на виявлення з залишку коштовного металу, який складає 0,5% його, а 1 г такого металу на світовому ринку коштує 15000 доларів?
5. Два фермери почали розраховуватись борошном за позики один від одного.

1-й: - Повертаю мішка борошна за бичка.

2-й: - Повертаю 60% цього твого боргу за твого теля.

1-й: - Повертаю 20% мішка, що брала жінка у твоєї жінки на випікання хлібу.

2-й: - Зменшую хлібну долю в 8 разів і повертаю назад. Моя жінка брала у твоєї борошно на млинці.

1-й: - 0,125 мішка віддаю за півня.

2-й: - Збільшую цю долю в три рази і повертаю за курку.

1-й: - 10%  мішка візьми назад за індика.

2-й: - В два рази менше візьми за гусака.

1-й: - мішка візьми за порося.

2-й: - Зменш цю долю в  разів та візьми назад за кроля.

Хто і кому скільки борошна винен?

6. Від двох шматків сплавів з різним вмістом міді, вага яких 15 кг і 10 кг, відрізали по шматку однакової ваги. Кожний з відрізаних шматків сплавили з залишком іншого шматка. Після цього процентний вміст міді в обох сплавах став однаковим. Скільки важив кожний з відрізаних шматків?
7. Є два зливки золота зі сріблом. Процентний вміст золота в першому зливку в два з половиною рази більший, ніж процентний вміст золота в другому зливку. Якщо сплавити обидва зливки разом, то вийде зливок, у якому буде 40% золота. Знайдіть у скільки разів перший зливок важчий другого, якщо відомо, що при сплавці рівних за вагою частин першого і другого зливків виходить зливок, у якому міститься 35% золота.
8. Сплав олова зі сріблом, що містить 5 кг срібла, сплавили з 15 кг срібла. У результаті відсоткові вмісти олова в новому і початковому сплавах стали відрізнятися на 30%. Знайти масу початкового сплаву.
9. У посудині було 10 л концентрованої сульфатної кислоти. Частину її відлили і посудину доповнили такою ж кількістю води. Потім знов відлили таку ж кількість суміші і доповнили посудину такою ж кількістю води. Скільки води доливали кожного разу, якщо в результаті в посудині утворився 64% розчин сульфатної кислоти?
10.                      До деякого задуманого двозначного числа, що закінчується нулем, дописали це ж число. Утворилось нове число, та з нього відняли квадрат задуманого числа. Різницю поділили на 4% від квадрату задуманого числа. Отримали частку половину задуманого числа, а в остачі задумане число. Яке це число?

 

 

Частина 4.

Переходимо до 9 класу. В 9 класі вивчається тема ” Відсоткові розрахунки ”, де розглядаються всі типи задач, з якими ми знайомилися раніше, і способи їх розв'язання. Але в цьому розділі є і нові підтеми, а саме ” Складні відсотки ”. Взагалі, цю тему краще було б розглядати після теми ” Геометрична прогресія ”, оскільки сама формула складних відсотків є ні чим іншим, як формулою (n-го члена).

 

    і   ,

де .

Представляємо набір задач, які можна використовувати на уроках для 9-го класу.

1. Перший внесок при придбанні квартири становить 10% її вартості, а на решту суми комерційний банк ” Печераінвест буд ” надає кредит терміном на 10 років під 5% річних від суми кредиту. Борг потрібно повертати протягом 10 років по 135 у.о. щомісяця. На скільки відсотків дорожче від початкової вартості коштує квартира у кредит?
2. Директор закритого акціонерного товариства з необмеженою безвідповідальністю ” Хап-Цап-Траст-Інвест ” пан Крутинець має щомісячний доход 10000 дуже умовних одиниць, які повністю кладе на свій банківський рахунок під 8% місячних. Оцінити величину його рахунку через 8 місяців після його відкриття, тобто зразу ж після 9 внеску.
3. Сума зовнішніх кутів опуклого многокутника складає 10% суми внутрішніх його кутів. Скільки сторін має многокутник?
4. За договором з компанією  бригада взялася пробурити свердловину глибиною 2000 м. Геологічні  умови дільниці такі, що перші 80 м були пробурені  за 100 хв., але потім з кожним новим метром приходилося витрачати на 2 % часу більше, ніж за попередній. Прийняв середню швидкість буріння на перших 80 м за початкову, знайти за скільки часу буде пробурена свердловина при таких умовах?
5. Чи є число,  28% якого складає 4,2, розв'язком нерівності ?
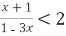6. Завод повинен був виготовити 1200 деталей за певний час. Через 15 днів після початку роботи коньюктура ринку показала збільшення попиту на вироби, а тому завод збільшив випуск продукції на 25%. Завдяки цьому і виготовлення деталей було завершено на 5 днів раніше терміну. Скільки деталей завод виконав додатково?
7. Вкладник поклав до банку 10000 грн. на депозитний рахунок під певний відсоток річних щорічно. Унаслідок економічного зростання через рік відсоток річних було збільшено на 4%. Наприкінці  другого року на рахунку цього вкладника було 12096 грн. Знайдіть початкову відсоткову ставку.
8. Площі чотирикутника  і трикутника складають відповідно 67% і 44% площі їх об'єднання. Скільки відсотків площі трикутника знаходиться за межами чотирикутника?

 

Та оскільки в 9 класі ми все ж повторюємо вивчене раніше, то можна використовувати задачі попередніх розділів, нами вже розглянутих, та додатково пропонуємо інші , на нашу думку, цікаві задачі.

 

1.    Розчин Y складається з 30% рідини X та 70% води. Якщо 2 л води випарувались з 8 л розчину Y, і до решти 6 л додали 2 л розчину Y, який відсоток нового розчину становить рідина X?
2.    З 3600 службовців компанії клерки. Якщо їх кількість скоротити на , який відсоток вони становитимуть від нової кількості службовців?
3.    Кількість робітників на фабриці після введення нової технології  скоротилась на 205, а кількість виробленої продукції зросла на 20%. На скільки відсотків зросла середня продуктивність одного робітника?
4.    У деякій країні пройшли вибори до парламенту. Всі ті хто голосував за партію ” Апельсин! ”, полюбляють апельсини. Серед тих хто голосував за інші партії або проти всіх, тільки десята частина полюбляє апельсин. Який відсоток голосів набрала партія ” Апельсин! ” на цих виборах, якщо відомо, що серед тих, хто проголосував, 46% полюбляють апельсин?
5.    Кількість розумних дівчат в Хацапетівці на 40% більша від кількості гарних. Відомо, що серед розумних 25% є гарними. Який відсоток гарних є розумними?
6.    У готелі села Хацапетівка ”Свіжість Ілліча” рівно 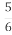кімнат кондиційовані. Однієї ночі зайнятими виявилися 75% усіх кімнат, і зокрема 80% усіх кондиційованих. Скільки відсотків з усіх некодиційованих кімнат було зайнято?

 

В наступних 10-11 класах з відсотками знов майже не зустрічаються. Але по-перше: учні повинні готуватись до ЗНО, а, по-друге: необхідно працювати над профорієнтацію учнів (особливо тих, хто збирається вступати на економічні напрямки).

Тому потрібно знаходити задачі, які б пов'язували матеріал цих класів з відсотками. Наприклад:

 

1. Довжину діагоналі куба збільшили на 100%; на скільки відсотків збільшилась його поверхня?
2. На скільки відсотків треба збільшити радіус основи циліндра, щоб його об'єм збільшився на 96%?
3. Будка Тузика має форму прямокутного паралелепіпеда. Хазяїн будки збільшив довжину будки на 10%, ширину - на певну кількість відсотків, а висоту – на вдвічі більшу кількість відсотків ніж ширину. В результаті об'єм будки збільшився на 84,8%. На скільки відсотків було збільшено висоту будки?
4. Якщо населення деякої держави щорічно збільшується на 2%, то через N років населення потроїться. N=…?

 

Або пошукати задачі, які розв’язують у ВНЗ. Пропонуємо для розв’язання, задачі Київського національного економічного університету, що входять до теми   ”Числова послідовність”.

1.    Обладнання вартістю 10000 гривень внаслідок експлуатації втрачає кожного року 20% своєї вартості. Знайти кількість років його доцільного використання, якщо при вартості 3000 гривень обладнання використовувати недоцільно.
2.    Кожного року чоловік вкладає 1000 гривень для накопичення з фіксованим 8% щорічним зростанням. Скільки коштів він буде мати через 10 років?
3.    В день 60-річчя містер Стоун відкрив рахунок ренти в страховій компанії на своє ім’я з умовами, що він буде одержувати щорічно на свій день народження, починаючи з наступного року 5000доларів на протязі 10 років. Компанія прийняла його кошти і відкрила йому рахунок ренти з щорічним зростанням на 8%. Яку суму внесено на рахунок ренти містера Сміта?
4.    На час навчання студент університету отримав з фонда навчання в борг 8000 доларів. Цей займ йому надано із 8% щорічного зростання і умовою щорічного повернення боргу в кінці кожного року після закінчення університету на протязі 5 років. Скільки коштів повинен повернути студент кожного року після закінчення університету?

 

Як бачимо з останніх задач, усі вони розглядалися в школі, а отже, таким чином учні побачать зв’язок не тільки між темами в школі, а і зрозуміють їх значення в майбутньому.

Сподіваємось, що ця робота допоможе всім, хто зацікавився темою ”Відсотки”. Учням – більш детально її розібрати, вчителям – більш доступно її пояснити. Бажаємо успіхів!

 

Список використаної літератури:

 

1. Бондарчук Ю. В., Братик М. В., Захарійченко Ю. О., Кашпіровський О. І., Митник Ю. В., Пилявська О. С., Черкасенко В. П. Математика. Вступні тести. Тренувальні задачі / Ю. В. Бондарчук. — К. : Видавничий дім «Києво-Могилянська Акдемія», 2005. —216 с.
2. Бурда М. І. Збірник завдань для державної підсумкової атестації з математики. 9 клас / М. І. Бурда, О. П. Вашуленко, Н. С. Прокопенко. — Х. : Гімназія, 2010. — 256 с.
3. Гайштут А. Г. Математика в логических упражнениях / А. Г. Гайштут. — К. : Рад. шк., 1985. — 192 с.
4. Грицаенко Н. П. Попробуй, реши! Учебное пособие для детей среднего и старшего школьного возраста / Н. П. Грицаенко. — Днепропетровск : МП «Промінь», 1995. — 128 с.
5. Захарійченко Ю. О. Повний курс математики в тестах / Ю. О. Захарійченко, О. В. Школьний, Л. І. Захарійченко, О. В. Школьна. — 3-те вид. — Х. : Вид-во «Ранок», 2013. — 496 с. — (Енциклопедія тестових завдань).
6. Захарійченко Ю. О., Школьний О. В. Математика: збірник тестових завдань для абітурієнтів / Ю. О. Захарійченко. — К. : Видавничий дім «Києво-Могилянська Акдемія», 2006. — 230 с.
7. Збірник задач з математики ля вступників до втузів / за редакцією М. І. Сканаві. — Мінськ : Вишейш. Шк.., 1990. — 528 с.
8. Кострикина Н. П. Задачи повышенной трудности в курсе алгебры 7-9 классов : Кн. для учителя / Н. П. Кострикина. — М. : Просвещение, 1991. — 239 с.
9. Кравчук В., Підручна М., Янченко Г. Алгебра. Пробний підручник для 8 класу / за редакцією З. І. Слєпкань. — Тернопіль : Підручники і посібники, 2003. — 224 с.
10.                    Макаренко В. О., Бех О. В. Методичні вказівки до самостійного вивчення теми «Числова послідовність» та виконання індивідуальних завдань / В. О. Макаренко. — Кривий ріг : Криворізький економічний інститут КНЕУ, 2001 —46 с.
11.                    Мерзляк А. Г. Алгебра : підруч. Для 9 кл. з поглибл. вивч. математики / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. — Х. : Гімназія, 2011. — 384 с. : іл..
12.                    Русанов В. Н. Математические олимпиады младших школьников : Кн. для учителя: Из опыта работы (в сел. Р-нах) ./ В. Н. Русанов. — М. : Просвещение, 1990. — 77 с.
13.                    Ясинський Математика. Навч. посібник для слухачів підготовчих курсів ФДП НТУУ «КПІ» / В. В. Ясінський. — К. : вид. Гнозіс, 2014. — 472 с. —(Серія «На допомогу абітурієнту»)