Степінь з натуральним показником. Властивості степеня з натуральним показником

Вчитель: Заєць Марія Олександрівна

Урок Алгебри у 7 класі

Тема: «Степінь з натуральним показником. Властивості степеня з натуральним показником.»

Мета: систематизувати та узагальнити знання учнів про означення та властивості степеня числа з натуральним показником; удосконалити вміння використовувати властивості степенів для розв'язування задач, формувати навички усних розрахунків;  формувати вміння правильно і чітко висловлювати влас­ні думки, формулювати математичні твердження; виховувати дисциплінованість, позитивне ставлення до знань

Тип уроку: засвоєння нових знань, умінь, навичок.

Обладнання: підручник, комп’ютер, мультимедійна презентація, плакат, опорні схеми, тести.

Девіз уроку: Думай і роби, роби і думай.

                                                         І. А. Крилов.

Епіграф: «Немає недосяжних цілей – є високий коефіцієнт ліні, недолік кмітливості і запас відмовок…» - тож працюватимемо і шукатимемо наш шлях до вивчення математики!

Хід уроку

1. Організаційний момент.

Привітання вчителя з учнями, перевірка готовності до уроку.

2. Перевірка домашнього завдання.

Онлайн-тестування за посиланням:

https://naurok.com.ua/test/osnovna-vlastivist-drobu-skorochennya-drobiv-14027.html

3. Мотивація навчальної діяльності учнів.

Історична довідка

Поняття степеня з натуральним показником сформувалося ще у давні часи. Квадрат числа використовували для обчислення площ, куб числа - для обчислення об’ємів. У Давньому Єгипті та Вавилоні степені деяких чисел використовували під час розв’язування окремих задач. Французький математик Франсуа Вієт використовував букви N, Q і С не лише для записів відповідно х, х² і х³, а й для запису степенів, вищих за третій. Наприклад, четвертий степінь у його записі виглядав так: QQ. Сучасний запис степенів запропонував видатний французький математик, фізик, філософ Рене Декарт. У своїй праці «Геометрія», датованій 1634 роком, він став записувати степені з натуральним показником так, як ми це робимо зараз: с³, с⁴, с⁵ і т. д. Проте с² він записував як добуток: сс. 

Рене Декарт                                            Француа Вієт

4. Актуалізація опорних знань.

Фронтальне опитування:

•                      Що таке квадрат числа? Куб числа?
•                      Як по іншому можна записати 5*5*5*5, 3*3*3*3*3*3?
•                      Що означає 4², 6⁵?

5. Вивчення нового матеріалу. Формування вмінь.

План:

1. Означення степеня з натуральним показником, більшим за 1.
2. Термінологія ( назва елементів запису, з яких складається степінь).
3. Піднесення до степеня як п’ята арифметична дія.
4. Знак степеня з натуральним показником n.
5. Властивості степенів з натуральним показником.

1. Означення степеня з натуральним показником, більшим за 1

Означення 1. Степенем числа а з натуральним показником n (n > 1) називають добуток n множників, кожний з яких дорівнює а.

Означення 2. Степенем числа а з показником 1 називають саме числа а.

Вираз аⁿ читають так: «а в степені n» або «n- енний степінь числа а».  Вирази а² і а³ називають відповідно квадратом числа а і кубом числа а.

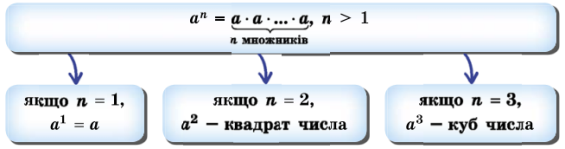
2. Термінологія ( назва елементів запису, з яких складається степінь)

Приклад 1. Прочитайте вирази, назвіть основу і показник степеня:

3. Піднесення до степеня як п’ята арифметична дія

Обчислення значення степеня є арифметичною дією, яку називають піднесенням до степеня.

У виразах, що містять степені, спочатку виконують піднесення до степеня, потім — множення або ділення, а останніми — додавання або віднімання. Тут і далі буквені показники є натуральними числами

Приклад 2. Виконати піднесення до степеня:

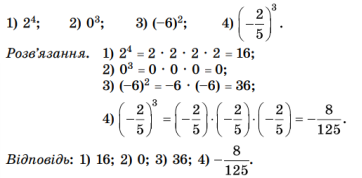
Приклад 3. Знайти значення виразу:

4. Знак степеня з натуральним показником n

Знак степеня залежить від знака основи степеня та від парності чи непарності показника степеня.

Наприклад, значення 5³ є додатним числом, а значення (-5)³ є від’ємним числом, тому:  5³ > (- 5)³.

5. Властивості степенів з натуральним показником

1. Множення степенів з однаковими основами:

Щоб помножити степені з однаковими основами, основу залишають тією самою, а показники степенів додають.

Наприклад, З⁷ ∙ З⁵ = 3⁷⁺⁵ = З¹²;   а⁷а²а³ = а⁷⁺²⁺³ = а¹²

2. Ділення степенів з однаковими основами:

Щоб поділити степені з однаковими основами, основу залишають тією самою, а показники степенів віднімають.

Наприклад, З⁷ : З⁵ = 3^7-5 = З²;   а⁷ : а² = а^7-2= а⁵

3. Піднесення степеня до степеня

Щоб піднести степінь до степеня, основу залишають тією самою, а показники степенів перемножують.

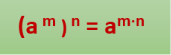
 Наприклад, (З⁷) ⁵ = 3^7∙5 = З^35;      ((З²) ⁵ )⁷= 3^2∙5∙7 = З⁷⁰

4. Піднесення добутку до степеня:

Щоб піднести добуток до степеня, потрібно піднести до цього степеня кожний з множників і отримані результати перемножити.

Наприклад, (7ab)² = 7²а²Ь² = 49а²Ь²

Властивості

6. Фізкультхвилинка.
7. Закріплення вивченого матеріалу .

Усні вправи:

1). Прочитайте вирази, назвіть основу і показник степеня:

2). Подайте добуток у вигляді степеня:

3). Яка з рівностей правильні:

Письмові вправи (робота з підручником):

Виконання вправ першого – третього рівня складності.

8. Підсумки уроку.

Сьогодні на уроці ми ознайомилися з поняттями «степінь», «властивості степенів» та навчилися розв’язувати задачі та вправи з степенями.

Запитання:

1.               Які завдання виявилися цікавими?
2.               Які завдання були для вас за складними?
3.               Чи задоволені ви своєю роботою на уроці?
4.               Що таке степінь числа з натуральним показником?
5.               Назвіть властивості степенів?

9. Домашнє завдання.

1.     Опрацювати параграф 6-7;
2.     Розглянути приклади розв’язування степенів (приклад 1-3);
3.     Виконати номери: 314, 350.