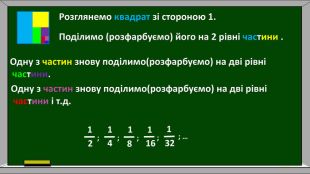
Сума нескінченної спадної геометричної прогресії
Про матеріал
Презентація "Сума нескінченної спадної геометричної прогресії" призначена для учнів 9 класу, які вивчають алгебру за підручником А.Г. Мерзляка на поглибленому рівні. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра (підручник для класів із поглибленим вивченням математики) 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
§ 7. Числові послідовності Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку