Сума перших n членів арифметичної прогресії.

Про матеріал

Актуалізувати знання учнів про арифметичну прогресію, формули для знаходження n-го члена арифметичної прогресії вивести формулу Sn для арифметичної прогресії; сформувати вміння застосовувати цю формулу до розв'язування задач, навчати учнів обчислювати суму перших n членів арифметичної прогресії.

Перегляд файлу

Тема: Сума перших n членів арифметичної прогресії.

Підготувала:

вчитель математики

Манявського ліцею

Федоришин Наталія Дмитрівна

лютий 2019р.

Тема уроку: Сума перших n членів арифметичної прогресії.

Мета уроку: навчальна: Актуалізувати знання учнів про арифметичну прогресію, формули для знаходження n-го члена арифметичної прогресії вивести формулу S_n для арифметичної прогресії; сформувати вміння застосовувати цю формулу до розв'язування задач, навчати учнів обчислювати суму перших n членів арифметичної прогресії.

розвивальна: розвивати системність і послідовність мислення, математичне мовлення, логіку.

виховна: виховувати математичну культуру, позитивну мотивацію до навчання.

Формування ключових компетентностей:

- формувати вміння відбирати й використовувати потрібні знання та способи діяльності для досягнення мети;

- формувати вміння оперувати числовою інформацією;

- сприяти самовихованню об'єктивності, чесності, відповідальності, принциповості.

Хід уроку

І. Організаційний етап

Перевірка готовності учнів до уроку, налаштування на роботу.

ІІ. Перевірка домашнього завдання

ІІІ. Актуалізація опорних знань.

Прогресії є відображенням світу, що нас оточує. Застосовується прогресія в таких науках, як:

- фізика: під час вивчення тіл, що вільно падають чи рухаються рівноприскорено, під час вивчення процесу радіактивного розпаду;

- економіка та банківська справа: під час виплати відсотків та надання кредитів; - у техніці: під час виготовлення обладнання.

Отже, ми розуміємо актуальність того, над чим працюємо для виконання завдань ДПА, домашніх завдань, тематичного оцінювання, тощо. Сьогодні на уроці ми закріпимо ваші знання з теми арифметична прогресія і дізнаємось як знаходити суму перших n членів арифметичної прогресії.

Бліц- опитування

1. Дайте означення арифметичної прогресії.

2. Що називають різницею арифметичної прогресії? Як позначають?

3. Назвіть формулу n-го члена арифметичної.

4. Які властивості арифметичної прогресії?

5. Який спосіб задання арифметичної прогресії ви знаєте?

6. Які бувають арифметичні прогресії?

Тестові завдання

1. Яка з послідовностей є арифметичною прогресією?

А) 4; 2;0;-1;... Б) 4;2;0;-2;... В) 4;2;1;-1;.... Г) 4;1;-2;-4;....

2. Яка з послідовностей є арифметичною прогресією?

А) 6;3;0;-4;... Б) 6;2;0;-2;.... В) 6;3;1;-3;.... Г) 6;3;0;-3;....

3. (a_n) - арифметична прогресіяa₁=-2, a₃=4 Знайдіть різницю прогресії

А) -6; Б) 3; В) 6; Г) 1.

4. (a_n) - арифметична прогресіяа₂=5, d=-3. Знайдіть: a₄.

А) -4; Б) -1; В) 2; Г) 8.

5. (a_n) - арифметична прогресіяa₁=8, a₄=-4 Знайдіть різницю прогресії

А) 4; Б) -12; В) -4; Г) -3.

6. (a_n) - арифметична прогресіяа₃=5, d=-4. Знайдіть: a₅.

А) 1; Б) -3; В) 3; Г) -7.

Відповіді: 1. Б); 2. Г); 3. Б); 4. Б); 5. В); 6. Б).

ІV. Формулювання мети і завдань уроку. Мотивація навчальної діяльності.

Актуальна задача

На шоу талантів 'Голос країни' після виступу всіх учасників глядачі протягом 30 хвилин могли взяти участь в смс - голосуванні за улюбленого учасника. Протягом першої хвилини від початку свою думку висловили 4800 глядачів. Протягом кожної наступної хвилини голосувало на 160 глядачів менше, ніж попередньої хвилини.

Запитання учням:

1. Скільки глядачів проголосували протягом другої хвилини від початку голосування?

2. Скільки глядачів проголосували протягом третьої хвилини від початку голосування?

3. Складіть формулу, за якою обчислюється кількість глядачів, які проголосували протягом n-ї хвилини від початку голосування (1 ≤ n ≤ 30).

4. Скільки глядачів проголосували протягом 30 хвилин від початку голосування?

Розв'язання:

а₁=4800, d=-160 a₂=4800-160=4640;

a₃=4800- 2∙160=4480; a_n= 4800-160 ∙(n-1);

a₃₀=4800-160∙29=160;

S₃₀=

Відповідь: 74400 глядачів проголосували протягом 30 хвилин.

V. Вивчення нового матеріалу.

План

1. Виведення формули суми перших n членів арифметичної прогресії.

2. Приклади застосування формули суми перших n членів арифметичної прогресії ( розв'язання актуальної задачі).

1. Розглянемо арифметичну прогресію: 1,2,3,....,98 , 99, 100 і знайдемо суму її членів.

Запишемо шукану суму двома способами та додамо отримані рівності:

S₁₀₀= 1+ 2+ 3+ ...+ 98 + 99 + 100

+ S₁₀₀=100+ 99+ 98+... +3 +2 + 1

2S₁₀₀=101+101+101+....+101+101+101 таких доданків є 100, тому

2S₁₀₀=101∙100; S₁₀₀=5050.

Скористаємось описаним прийомом для знаходження суми перших n членів арифметичної прогресії. Маємо:

S_n= a₁+(a₁+d)+ (a₁+2d) +(a₁+3d)+....+(a₁+(n-2)d)+ (a₁+(n-1)d),

S_n= a_n+ (a_n-d)+ (a_n-2d) + (a_n -3d)+....+(a_n- (n-2)d)+ (a_n- (n-1)d) додавши ці рівності , отримаємо:

2S_n=(a₁+a_n) +(a₁+a_n) +(a₁+a_n)+....+ (a₁+a_n)+ (a₁+a_n) і таких додонків є n,

тому 2S_n= (a₁+a_n)∙n, тобто або

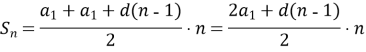
Задача 1. Знайти суму перших тридцяти членів арифметичної прогресії -23, -20,…

Розв’язання

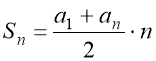
Щоб застосувати формулу потрібно знайти і .

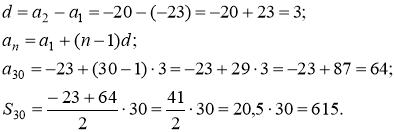Відповідь:615.

VІ. Формування вміння застосовувати виведену формулу до розв’язання задач

Робота в групах

Завдання І групі:

1.Чому дорівнює сума семи перших членів арифметичної прогресії (а_n), якщо

а₁=9 і а₇=15?

2. Знайдіть суму перших 27 членів арифметичної прогресії, у якої а₁=5 і d=3.

3. Знайдіть суму перших ста непарних чисел.

Завдання ІІ групі:

1.Чому дорівнює сума дев'яти перших членів арифметичної прогресії (а_n), якщо

а₁=4 і а₉=18?

2. Знайдіть суму перших 12 членів арифметичної прогресії, у якої а₁=-6 і d=4.

3. Знайдіть суму усіх парних чисел, що містяться від 1 до 100.

Завдання ІІІ групі:

1.Чому дорівнює сума шести перших членів арифметичної прогресії (а_n), якщо

а₁=20 і а₆=15?

2. Знайдіть суму перших 14 членів арифметичної прогресії, у якої а₁=7 і d=-3.

3. Знайдіть суму усіх натуральних чисел, кратних 4, що не перевищують 100.

Розв'язки до завдань:

І група

1. S₇=;

2. S₂₇=;

3. S₁₀₀=

II група

1. S₉=

2. S₁₂=

3. S₅₀=

III група

1. S₆=

2. S₁₄=

3. S₂₅=

Правильне розв'язання завдань дозволить учням відкрити по три букви на дошці, в результаті учні зможуть прочитати прізвище відомого німецького математика Карла Гаусса. Коротко його автобіографію розповість учениця.

Дитинство

Карл Фрідріх Ґаус народився 30 квітня 1777 р. у Брауншвейгу

— одному з німецьких князівств, які на той час ще не були об'єднані в єдину централізовану державу. Батько Карла спочатку працював слюсарем, а згодом став садівником, суміщаючи це заняття з обов'язками рахівника в торговельній конторі якогось купця. Він був людиною суворою, навіть грубою. Мати Карла була дочкою каменяра; від природи вона була жінкою розумною, розважливою, доброю і веселою. Карл був її єдиною дитиною, і вона безмежно та щиро любила його. Син відповідав їй такою самою гарячою любов'ю. Від матері він успадкував розважливість і м'яку вдачу.

Читати і писати Карл навчився сам: йому досить було знати лише кілька букв, підказаних матір'ю, щоб цілком оволодіти технікою читання. Вже в ранньому дитинстві у хлопчика виявились особливі здібності до математики. Пізніше він сам жартома говорив: «Я навчився рахувати раніше, ніж розмовляти». Розповідають про такий випадок. Якось до батька Карла зібралися товариші по роботі, щоб розподілити зароблені за тиждень гроші. Тут же був і трирічний Карл. Коли батько закінчив розрахунки, які він проводив уголос, щоб усі чули їх, і оголосив наслідки, Карл вигукнув: «Татку, ти помилився!» Присутні були вражені заявою малої дитини, але батько підрахував усе спочатку. Коли він назвав нову цифру (а раніше він справді зробив помилку), Карл радісно вигукнув: «Тепер правильно!»

Освіта

У 1784 р. Карла віддали до народної школи. Перші два роки навчання він нічим не відзначався серед товаришів, його виняткові здібності до арифметики виявилися у третьому класі. Якось учитель дав учням досить складне завдання з арифметики: відшукати суму 40 натуральних послідовних чисел. Учитель вважав, що учні досить довго шукатимуть відповідь. Але через кілька хвилин Карл розв'язав задачу. Коли вчитель проглянув розв'язання, то побачив, що малий Ґаус винайшов спосіб скороченого знаходження суми членів арифметичної прогресії. Цьому вченому належить дуже багато праць, він зробив величезний внесок у розвиток математики. $Описание: C:\Users\Viper\Desktop\468px-Carl_Friedrich_Gauss.jpg$

У 7 років Карл Гаусс пішов до школи. Якось учитель дав учням досить складне завдання: додати всі числа від 1 до 100. Учитель вважав, що учні досить довго шукатимуть відповідь. Коли вчитель проглянув розв’язання, то побачив, що маленький Гаусс винайшов спосіб скороченого знаходження суми членів арифметичної прогресії.

— Як ти підрахував?

— Дуже просто, — відповів хлопчик.

Я додав 1 до 100, одержав 101. Потім додав 2 до 99, теж одержав 101 і так 50 доданків по 101 кожний. Помноживши 101 на 50, одержав 5050.

S=1+2+3+…+99+100

S=100+99+...+2+1

____________________

2 S=

=5050

Здивований учитель зрозумів, що зустрів найобдарованішого учня в своєму житті. Отже, К.Гаусс обчислив суму 100 перших членів арифметичної прогресії. І саме суму потрібно знайти в історичних задачах. Причому для знаходження цих сум математики давно не користувались безпосереднім додаванням; для цього вони застосовували формули.

Робота з підручником

№ 17.5

a₁=6, d=3

a₁₆=6+3∙15=51

S₁₆=

Відповідь: 456 місць у секторі.

№ 17.17 (задача з папірусу Рінда)

a₁- 1 людина

а₁+d - 2людина всі разом 100м хліба

а₁+2d - 3 людина

а₁+3d - 4 людина

а₁+4d -5 людина

5а₁+10d=100,

14;

;

Відповідь: .

Чи знаєте ви, що таке магічний квадрат? Квадрат, що полягає з 9 кліток, у нього вписують числа, так щоб сума чисел по вертикалі, горизонталі діагоналі була тим самим числом- constanta.

9	19	5
7	11	15
17	3	13

Зауваження про арифметичну прогресію саме по собі дуже цікаво. Справа в тому, що з кожних дев'яти послідовних членів будь-якої арифметичної прогресії натуральних чисел можна скласти магічний квадрат.

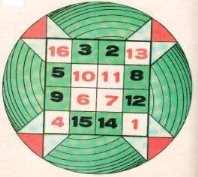Магічні квадрати.

VІІ. Домашнє завдання

Вивчити п. 17

Розв’язати № 17.2, 17.4, 17.6, 17.10 - обов'язково;

№ 17.22^* - додатково.

VІІІ. Підсумок уроку

На дошці записано всі натуральні числа від 1 до 50,крім чисел, кратних 5. Виберіть із них такі п’ять, які б утворили б арифметичну прогресію.

1,2,3,4,6,7,8,9,11,12,13,14,16,17,18,19,21,22,23,24,26,27,28,29,31,32,33,34,36,37,38,39,41, 42,43,44,46,47,48,49.

Відповіді: (1,11,21,31,41); (2,12,22,32,42); (3,13,23,33,43); (4,14,24,34,44); (6,16,26,36,46); (7,17,27,37,47); (8,18,28,38,48); (9,19,29,39,49).

docx

Завантажити

Зберегти на потім

Додав(-ла)

Федоришин Наталія Дмитрівна

Пов’язані теми

Алгебра, 9 клас, Розробки уроків

До підручника

Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)

До уроку

17. Сума n перших членів арифметичної прогресії

Додано

21 січня 2020

Переглядів

13180

Оцінка розробки

Відгуки відсутні