ТЕМА."СИСТЕМИ ЛІНІЙНИХ НЕРІВНОСТЕЙ З ОДНІЄЮ ЗМІННОЮ."

ТЕМА.СИСТЕМИ ЛІНІЙНИХ НЕРІВНОСТЕЙ З ОДНІЄЮ ЗМІННОЮ.                                                                     МЕТА: удосконалити вміння розв’язувати системи лінійних нерівностей з однією змінною;розвивати логічне мислення,  пам'ять, увагу;виховувати  почуття патріотизму, інтерес до математики, відповідальність.

Тип уроку: удосконалення знань і вмінь.

Обладнання та наочність: картки з завданнями, картки оцінювання учнів, портрет М.П. Кравчука.

Епіграф до уроку: Моя любов – Україна і математика.

Хід  уроку

׀. Організаційний етап.

Учні я хочу , щоб ви налаштувались на роботу.

                   Сьогодні ви повинні

                   Не просто слухати , а чути ,

                   Не просто дивитися , а бачити,

                    Не просто відповідати, а міркувати,

                   Дружно і плідно працювати.

║. Перевірка домашнього завдання.

1. Перевірити правильність виконання домашніх вправ за записами  зробленими до початку уроку.

                             Вправа 164

А)                          Б)                            В)            Г)

 

В-дь:(-∞;-4).           В-дь: розв’язків немає.       В-дь:[3;+∞).  В-дь:[-1;5).

                       Вправа 162

А) ні;                       Б)так;                В)ні.

                            Вправа187

у=4-0=4;

у=-14;

у=-14.

Так.

2. Математичний диктант.

(На дошці до початку уроку записана система нерівностей з однією змінною.)

Дано систему нерівностей з однією змінною:

׀ варіант -  ׀׀варіант -

 

                               Запишіть:

А) яке з чисел  -  1, 4 є розв’язком першої нерівності;

Б) яке з чисел – 4, 1 є розв’язком другої нерівності;

В) яке з чисел – 4, 1 є розв’язком системи;

Г) нерівність , рівносильну і простішу за першу нерівність системи;

Д) розв`язок  першої нерівності системи у вигляді проміжку;

Е) нерівність , рівносильну і простішу за другу нерівність системи,

Є) розв`язок другої нерівності системи у вигляді проміжку;

Ж) розв`язок системи у вигляді проміжку.

                               Відповіді:

׀ варіант  А) 1; 4; Б) 1; 4; В) 1;4; Г) х<5; Д) (-∞;5); Е) х≤7; Є)(-∞;7]; Ж) (-∞;5).

‖  варіант А) 1;4; Б) 4; В) 4; Г) Д) [1;+∞); Е)х>3; Є) (3;+∞); Ж) (3;+∞).

 (Учні перевіряють .)

׀׀׀. Актуалізація опорних знань.

Дайте відповіді на запитання:

1. Що називається розв’язком системи нерівностей з однією змінною? ( Розв`язком системи нерівностей з однією змінною називають значення змінної, яке задовольняє кожну з нерівностей даної системи.)
2. Що означає розв’язати систему нерівностей з однією змінною? ( Розв`язати систему нерівностей – це означає знайти всі її розв`язки або показати що їх немає.)
3. Назвіть кроки розв`язування системи лінійних нерівностей з однією змінною:

1. (Розв’язуємо  кожну нерівність системи );
2. (Зображуємо множину розв’язків кожної нерівності на одній координатній прямій.);
3. ( Знаходимо переріз множин розв’язків нерівностей і записуємо множину розв’язків системи у вигляді проміжку або відповідної нерівності.)

4. Що таке переріз числових проміжків? ( Називають множину всіх чисел , які належать кожному з цих проміжків.).

׀˅. Удосконалення знань і вмінь.

1. Гра «Математичне доміно»

( Розв`яжіть систему нерівностей.)

                          Старт

             │     (3;4)

 

              │     (3;+∞)

 

           │      Розв`язку немає

 

          │      (-2; 0]

 

         │      [5; +∞)

 

      │      (-∞;+∞)

 

           │      (-∞;3)

 

           │     [3;6)

 

         │      (-∞;1]

 

         │      (-∞;2)

 

                        │       (-∞;2)

 

2. Групи працюють з картками.

                       1 картка

Розв`яжіть систему нерівностей і вкажіть найбільше ціле число, яке є її розв’язком:

Розв`язання.

В-дь: (-3;4); 3.

                           2 картка

Знайдіть натуральні розв`язки системи нерівностей:

Розв`язання.

Х є (-∞;-4].

В-дь: таких розв’язків немає.

                                  3 картка

Розв`яжіть систему нерівностей:

Розв`язання.

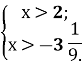
В-дь(2;+∞).

                             4 картка

Розв`яжіть систему нерівностей:

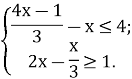
Розв`язання.

В-дь:[0,6;13].

3. Михайло Пилипович Кравчук.

Михайло Пилипович Кравчук народився 30 вересня 1892 р. в селі Човницях на Волині в сім`ї землеміра сина селянина-швейця. Початкову освіту  здобував у дома.

      В 1901 р. він разом з батьками перебирається до Луцька, де в 1910 р. закінчує з золотою медаллю гімназію. Цього ж року він вступає на фізико-математичний факультет Університету Святого Володимира в Києві . Тут його звільнили від плати за навчання, бо він складав іспити на відмінно, також отримує стипендію 50 карбованців. Закінчує університет і після закінчення викладає математичні дисципліни  в гімназіях у Києві.

       Одна за одною з`являються друковані праці Михайла Кравчука. Він автор  понад 180 наукових робіт. Його наукові результати дістали міжнародне визначення серед них і перший проект компютера.

Михайло Кравчук свою різнобічну наукову діяльність розглядав як справу патріотичну , як справу громадянську.  «Моя любов – Україна і математика» - любив наголошувати він.

  Він відомий ще й тим , що першим в Україні почав писати математичні праці українською мовою , за що був засуджений  до 20 років в’язниці та 5 років заслання , де 9 березня  1938 р. його  не стало.

Додаткові завдання.

4. Розв`язування задач.

        5 картка

Якщо до подвоєного цілого числа додати його половину , то одержимо число менше за 92 , а якщо із подвоєного того самого цілого числа відняти його половину , то одержимо число більше від 53. Знайти це ціле число.

Розв`язання.

Нехай х- шукане ціле число. Тоді , за умовою задачі маємо  систему

 

 

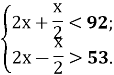
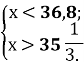
В-дь:36.

           6 картка

Якщо туристи будуть проходити за день на 5 км більше, то вони пройдуть за 6 днів відстань більшу від 90 км. Якщо ж  вони будуть проходити за день на 5 км менше, то за 8 днів  вони пройдуть відстань меншу 90 км. Скільки кілометрів в день проходять туристи?

Розв`язання.

Нехай х км проходять в день. Тоді, за умовою задачі маємо систему

В-дь:більше 10 км і менше 16

˅. §7 Впр 168(а,б);170(а,б);174(а,б).

V׀. Підсумок уроку.

Оцініть свою роботу на уроці. Висловіть свої відчуття від уроку за допомогою рук. Задоволений – «аплодуй», байдужий – «позіхай», сердитий – «тупочи».

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

        Михайло Пилипович Кравчук народився 30 вересня 1892 р. в селі Човницях на Волині в сімї землеміра сина селянина-швейця. Початкову освіту  здобував у дома.

       В 1901 р. він разом з батьками перебирається до Луцька, де в 1910 р. закінчує з золотою медаллю гімназію. Цього ж року він вступає на фізико-математичний факультет Університету Святого Володимира в Києві . Тут його звільнили від плати за навчання, бо він складав іспити на відмінно, також отримує стипендію 50 карбованців. Закінчує університет і після закінчення викладає математичні дисципліни  в гімназіях у Києві.

        Одна за одною зявляються друковані праці Михайла Кравчука. Він автор  понад 180 наукових робіт. Його наукові результати дістали міжнародне визначення серед них і перший проект компютера.

Михайло Кравчук свою різнобічну наукову діяльність розглядав як справу патріотичну , як справу громадянську.  «Моя любов – Україна і математика» - любив наголошувати він.

  Він відомий ще й тим , що першим в Україні почав писати математичні праці українською мовою , за що був засуджений  до 20 років в’язниці та 5 років заслання , де 9 березня  1938 р. його  не стало.