Урок. "Інтеграл та його застосування."

Тема уроку:  Інтеграл та його застосування.

Мета уроку: удосконалюючи,систематизувати й узагальнити знання, вміння та навички учнів використовувати інтеграл для обчислення визначених інтегралів, площ; показати можливість застосування інтеграла в різних галузях фізики, геометрії; розвивати  мислення;формування вміння робити висновки; виховувати потребу залучати власний досвід для розв’язування завдань, самостійність.

Тип уроку:   узагальнення і систематизація знань.

Обладнання:  ноутбук, роздавальний матеріал.

Хід уроку

І. Організаційна частина

ІІ. Перевірка домашнього завдання

Виконання тестових завдань

 «Інтеграл та його застосування»

Варіант 1

1.

A)-2 ; Б)2; В)12; Г)4.

2. = ?

 A)1 ; Б)-0,5; В); Г).

3.Знайдіть площу фігури обмежену лініями

у = у = 0; х = 1; х =9.

A)17 ; Б)9; В); Г)1.

4.Знайдіть об’єм тіла утвореного обертанням навколо осі х фігури, обмеженої заданими лініями у =х =4; у =0.

 A) ; Б); В)4; Г)8.

Варіант 2

1.

A)-2 ; Б)2,5; В)12; Г)39,5.

2. = ?

 A)- ; Б)-0,5; В); Г).

3.Знайдіть площу фігури обмежену лініями

у =у = 0; х = -1.

A) ; Б)9; В); Г)2.

4.Знайдіть об’єм тіла утвореного обертанням навколо осі х фігури, обмеженої заданими лініями у =х =9; у =0.

 A) ; Б); В)4; Г)8.

Відповіді: Варіант 1 (1)В, 2)Б, 3)А,4)Г). Варіант 2(1)Г, 2)А, 3)А,  4)В.)

ІІІ.  Мотивація навчальної діяльності, повідомлення теми й мети уроку

Евдокс Кнідський (бл. 408-355 рр. до н.е.) стародавній учений. Довів теорему про об’єм піраміди. Для доведення застосував метод «вичерпування», який через дві тисячі років був перетворений на метод інтегрування, за допомогою якого вдалося обчислити площі, об’єми, масу, роботу, тиск, електричний заряд тощо. Пізніше метод «вичерпування» застосував Архімед.

Термін «інтеграл» (від лат. Integer – цілий) був запропонований 1696 року Йоганном Бернуллі. Великий внесок у розвиток цього поняття зробили Ісаак Ньютон та Готфрід Лейбніц. Інтеграли використовують для розв’язування багатьох задач, і не тільки з математики.

Тема сьогоднішнього уроку «Інтеграл та його застосування». Мета уроку  «удосконалюючи,систематизувати й узагальнити знання, вміння та навички учнів використовувати інтеграл для обчислення визначених інтегралів, площ; показати можливість застосування інтеграла в різних галузях фізики, геометрії».

І˅. Актуалізація  опорних знань

Розминка: «Несправний диктофон». Учитель пропонує закінчити речення, 

щоб сформульовані твердження були вірними:                                

«Криволінійною трапецією називається…»

«Дія, обернена до диференціювання …»

«Первісні для однієї і тієї ж функції відрізняються тільки…»

«Визначений інтеграл відрізняється від невизначеного тим, що…»

«Функція записана  під знаком інтеграла, закінчується  знаками…»

«Геометричним змістом визначеного інтеграла є…»

«Фізичним змістом визначеного інтеграла є…»

«Шлях, пройдений тілом за проміжок часу, виражається через інтеграл так: S=…)

Це цікаво знати

А чи вірите ви, що площа «криволінійного чотирикутника» АВСД дорівнює площі одиничного квадрата, тобто 1. Ви дізнаєтесь відповідь, обчисливши площу «криволінійного чотирикутника» АВСД за допомогою формули Ньютона – Лейбніца.

 

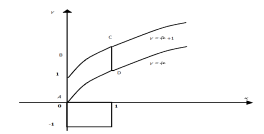
        Розв’язування простої, але не зовсім стандартної задачі може вимагати деякого напруження, натомість дає відчути тріумф відкриття.(Дьордь Пойа(1887-1985) – угорський,  швейцарський і американський математик.)

           Закінчуючи  11 клас, кожен з вас замислюється над вибором професії. Неабияку роль у цьому грає реклама. А чи знаєте ви, які професії пов’язані з рекламою?

         (Роздаю  учням пам’ятки про професії, пов’язані з рекламою, і пропоную учням завдання творчого характеру «Зроби рекламу теми «Інтеграл»».)

˅. Застосування теоретичного матеріалу до розв’язування задач

Зараз виконуємо завдання (працюємо в парах).

1.Гра «Чи правильно, що …?

Якщо учні погоджуються із твердженням, ставлять знак «+», якщо ні – знак «-».

1)

2) Визначений інтеграл – це площа криволінійної трапеції?  

3) ?

4)

5)

6)

(Відповіді:1)ні, 2)ні, 3)так,4)так,5) ні, 6)так.)

 

2. Запишіть за допомогою інтеграла площі фігур, зображених на рисунку .

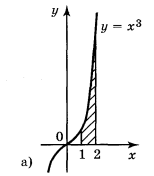
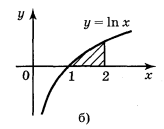
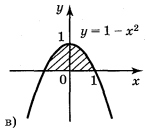
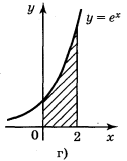
Рис.

 

Відповіді: а); б) ; в) ; г)  

3.Обчисліть об’єм тіла утворене обертанням навколо осі х фігури, обмеженої заданими лініями у= - +2х, у = 0.

4. Тіло рухається зі швидкістю v(t) = 3 -2t+3. Знайдіть шлях (у м), пройдений тілом за проміжок часу (у с) від =0 до = 2.

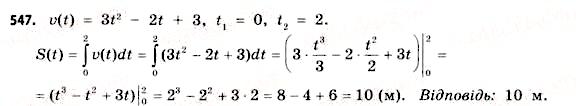
5. Для стиснення пружини на 1 см треба прикласти силу 9,8 Н. яку роботу треба виконати, щоб стиснути пружину на 4 см?

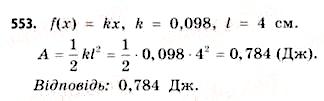
6. сила струму в провіднику з часом змінюється за законом І(t) = 4+2t. Яка кількість електрики пройде через поперечний переріз провідника за час від 2-ї до 6-ї секунди ?

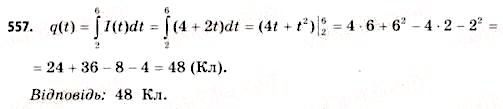
  Додаткове завдання 

7. Впр 549         

8. Знайдіть, при якому значенні а площа фігури, обмеженої параболою

 у =6 і прямими у = 0, х = а – 2, х = а, набуватиме найменшого значення.

Відповідь:а = 1.

˅ǀ. Підсумок уроку

          Щоб кожен міг з упевненістю сказати, що він досяг успіху, необхідно самостійно попрацювати. Адже китайська мудрість наголошує « … Покажи мені  ̶  і я запам’ятаю. Дай мені діяти самому  ̶  і я навчуся …».

          Усе людське життя  - це не  що інше, як постійне визначення мети та бажання досягти успіху під час розв’язування нових задач та проблем. Учіть свій розум та душу бачити добро, і тоді дорога до успіху буде для вас відкрита.

˅ǀǀ. Домашнє завдання

Повторити § 13-16. Впр 536, 550, 556.