Тематична контрольна  робота № 1 з теми

«Показникова функція» 

І варіант

ЧАСТИНА 1   / 5 балів /

Завдання 1 – 3  містять по 4 варіанти відповідей, з яких тільки ОДНА відповідь є ПРАВИЛЬНОЮ. Виберіть правильну, на вашу думку, відповідь і зазначте її в бланку відповідей.

1. Яка з наведених функцій є показниковою:
   А) y=x³;          Б) y=1^x;          В) y=(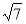)^x;           Г) y=5x+3.
2. Яка з наведених показникових функцій є спадною:
   А) f(x)=5^x;        Б) f(x)=0,2^x;       В) f(x)=^x;       Г) f(x)=.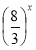
3. Якщо 4^m > 4ⁿ, то виконується умова
   А) m > n;     Б) m< n;     В) m = n;     Г) m  n.
4. Розв’яжіть рівняння: 

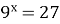
А)  х=3;          Б) х=-3;          В) х=1,5;           Г) х=-1,5.

5. Розв’яжіть нерівність:.

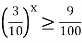А)  х≥2;          Б) х≥-2;          В) х≤2;           Г) х≤-2.

ЧАСТИНА 2    / 4 бали /

У завданнях 4 – 6 наведіть розв'язання.  Запишіть відповідь у бланк відповідей.

6. Розв’яжіть рівняння 5^х+3 = 625.
7. Розв’яжіть нерівність 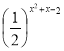≥ 4^х-1.

ЧАСТИНА 3     / 3 бали /

Розв’язання завдань 7 повинне містити повне пояснення, записане у вигляді послідовних логічних дій, із посиланням на математичні факти, з яких випливає те чи інше твердження.

8. Розв’яжіть рівняння 4^2х – 17 ∙ 4^х + 16 = 0.

Тематична контрольна  робота № 1 з теми

«Показникова функція» 

ІІ варіант

ЧАСТИНА 1   / 5 балів /

Завдання 1 – 3  містять по 4 варіанти відповідей, з яких тільки ОДНА відповідь є ПРАВИЛЬНОЮ. Виберіть правильну, на вашу думку, відповідь і зазначте її в бланку відповідей.

1. Яка з наведених функцій є показниковою:
   А) y=1^x;          Б) y= –x+9;          В) y=x⁶;           Г) y=(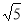)^x.
2. Яка з наведених показникових функцій є зростаючою:
   А) f(x)=0,5^x;        Б) f(x)=7^x;      В) f(x)=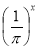;       Г) f(x)=.
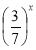3. Якщо 4^m < 4ⁿ, то виконується умова
   А) m > n;     Б) m< n;     В) m = n;     Г) m  n.
4. Розв’яжіть рівняння: 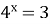 2;

А)  х=5;          Б) х=-5;          В) х=2,5;           Г) х=-2,5.

5. Розв’яжіть нерівність:.

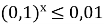А)  х ≥ 2;          Б) х ≥ -2;          В) х ≤ 2;           Г) х ≤ -2.

ЧАСТИНА 2    / 4 бали /

У завданнях 4 – 6 наведіть розв'язання.  Запишіть відповідь у бланк відповідей.

6. Розв’яжіть рівняння 2^х-5 = 64.
7. Розв’яжіть нерівність 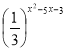≤ 9^х-3.

ЧАСТИНА 3     / 3 бали /

Розв’язання завдань 7 повинне містити повне пояснення, записане у вигляді послідовних логічних дій, із посиланням на математичні факти, з яких випливає те чи інше твердження.

8. Розв’яжіть рівняння 2^2х + 2 ∙ 2^х –24 = 0.