Тема уроку.   Теорема про існування і єдиність прямої, яка проходить через дану точку і паралельна даній прямій.

Мета уроку: вивчення теореми про існування і єдиність прямої, яка проходить через дану точку і паралельна даній прямій.

Обладнання: стереометричний набір, модель куба.

Хід уроку

І. Перевірка домашнього завдання

1. Фронтальне опитування.

1)Які прямі в просторі називаються паралельними?

2) Вкажіть пари паралельних прямих на зображенні куба ABCDA₁B₁C₁D₁.

3) Які прямі в просторі називаються мимобіжними?

4) Вкажіть пари мимобіжних прямих на зображенні тетраедра SABC.

5) Назвіть можливі випадки взаємного розташування двох різних прямих у просторі.

2. Перевірку правильності виконання задачі № 1 провести за записа­ми з пропусками, зробленими на дошці до початку уроку.

Розв'язання задачі № 1

Припустимо, що прямі АС і BD не..., тоді вони лежать в одній пло­щині, отже, точки... теж... в одній площині. Згідно з теоремою 1.2 прямі ... лежать в одній площині, що суперечить... . Отже, припущення непра­вильне. Таким чином, прямі ... мимобіжні.

II. Сприйняття й усвідомлення нового матеріалу

Теорема про існування і єдиність прямої, яка проходить через дану точку і паралельна даній прямій

З аксіоми паралельності Евкліда випливає, що в площині через дану точку можна провести не більше однієї прямої, яка паралельна даній прямій. А скільки таких прямих можна провести у просторі?

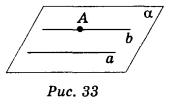
Нехай дано пряму a і точку А, що не ле­жить на ній. Через них можна провести єдину площину (теорема 1.1). У цій площині можна провести єдину пряму b, яка паралельна пря­мій α (рис. 33).

Отже, у просторі через дану точку А мож­на провести єдину пряму, паралельну даній прямій а.

Таким чином, справедлива теорема:

Через будь-яку точку простору, яка не лежить на даній прямій, можна провести пряму, паралельну даній, і тіль­ки одну.

Виконання вправ

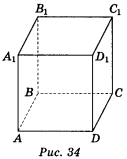
1. Користуючись зображенням куба ABCDA₁B₁C₁D₁ (рис. 34), вкажіть пряму, яка проходить через точку А₁ і паралельна прямій:  a) AD;   б) АВ;    в) АС.

2. Скільки прямих, паралельних даній прямій а, можна провести через точку А, що належить прямій а?

III. Закріплення та осмислення знань учнів

Формування вмінь застосовувати вивчену теорему та означення паралельних прямих до розв'язування задач

1. Задача № 4 із підручника (с. 18).

Розв'язання задачі

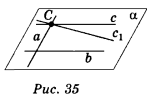
Нехай c — пряма, яка паралельна прямій b і перетинає пряму a (рис. 35). Проведемо че­рез прямі a і b площину α . Через точку С — точку перетину прямих a і c — проведемо пря­му c₁, паралельну прямій b. За теоремою 2.1 випливає, що пряма с, збігається з прямою с, отже, пряма с лежить у площині α . Таким чином, будь-яка пряма с, яка паралельна прямій b і перетинає пряму a, лежить у площині a.

2. Доведіть, що паралельні прямі, які перетинають дану пряму, ле­жать в одній площині.

3. Задача № 5 (2, 4) із підручника (с. 18).

4. Задача № 7 (2, 4) із підручника (с. 19).

5. Задача № б* (4) із підручника (с. 18).

IV. Домашнє завдання

§ 2, п. 7; контрольне запитання № 3; задачі: 5 (1, 3), 7 (1, 3) (с. 18—19).

V. Підведення підсумку уроку

Запитання до класу

1) Які прямі називаються паралельними?

2) Сформулюйте аксіому паралельних прямих.

3) Скільки прямих, паралельних даній прямій, можна провести у про­сторі через точку:

а) яка не належить даній прямій;

б) яка належить даній прямій?