Урок "Перпендикуляр та похила в просторі"

Тема. Перпендикуляр та похила у просторі

Мета: показати застосування перпендикуляра та похилої у просторі, їх властивостей, властивості точки, рівновіддаленої від вершин многокутника та  властивості точки, рівновіддаленої від сторін многокутника під час розв’язування задач; продовжити формування в учнів умінь і навичок використання вивчених ознак і властивостей до    розв’язування задач практичного змісту; розвивати логічне мислення, вміння аналізувати ситуацію, вміння використовувати власний досвід; виховувати зацікавленість до предмета геометрія, вміння працювати в групі, примати рішення, домовлятися, вміння організовувати роботу, нести відповідальність, бути стійким перед труднощами.

Тип уроку: засвоєння умінь, знань, навичок.

Обладнання: роздатковий матеріал, презентація, тест-онлайн.

Хід уроку

Організаційний момент

Перевірка домашнього завдання

   Вчитель перевіряє домашнє завдання.

Мотивація навчальної діяльності

   На сьогоднішньому уроці ми перевіримо ваші знання з теми «Перпендикуляр та похила у просторі» та вміння їх застосовувати на практиці до розв’язування вправ.

    Разом з цим перевіримо таку просту істину, визначену ще Конфуцієм: «Три шляхи ведуть до знань: шлях міркувань – це найблагородніший, шлях наслідування – шлях найлегший і шлях досвіду – це шлях найгіркіший». Цей вислів стане нашим девізом на уроці.

Повідомлення теми і мети уроку

Відповідно до мети уроку кожний із вас повинен поставити власні цілі, над досягненням яких і буде працювати на сьогоднішньому уроці. Подумайте,  які це будуть цілі, й обговоріть їх у групах.

А я пропоную вам хвилинку релаксації, щоб стати більш впевненим у своїх силах. Тому сядьте рівненько, закрийте очі, і уявіть, що ви опинились в зимовою лісі, тихо падає сніг, ви ніби летите, як та сніжинка до своєї мети, ось ваша мета зовсім поряд…Відкрийте очі. І досягніть цілі, поставленої вами сьогодні. (Музика)

Актуалізація опорних знань

Отже, для досягнення мети уроку і здобуття навичок у розв’язуванні задач, з  використанням властивостей перпендикуляра та похилої у просторі треба знати теоретичний матеріал. Тому  пропоную вам онлайн-тест.

 Закріплення вмінь і навичок

Робота в гомогенних групах

А тепер всі групи отримали різнорівневі завдання, які надруковані на картках, що лежать перед вами. Кожен член групи обирає собі той рівень складності, який вважає посильним для себе. Учні, що обрали завдання одного рівня, утворюють групу, займають вказане місце і приступають до роботи. По закінченню роботи один представник від кожної групи виходить до дошки і захищає рішення групи.

Рівень А

     З точки до площини проведено дві похилі, які дорівнюють 5 см і 4 см. Проекція однієї з цих похилих на 5 см більша за проекцію другої похилої. Знайдіть відстань від цієї точки до площини.

Рівень Б

З точки до площини проведено перпендикуляр та дві похилі, які

дорівнюють 10 см і 17 см, а їх проекції відносяться, як 2:5. Знайдіть довжину перпендикуляра.

Рівень В

Через вершину прямого кута прямокутного трикутника проведено площину на відстані 4 м до гіпотенузи, яка паралельна цій площині. Проекції катетів на цю площину дорівнюють 12 м і 20 м. Знайдіть гіпотенузу.

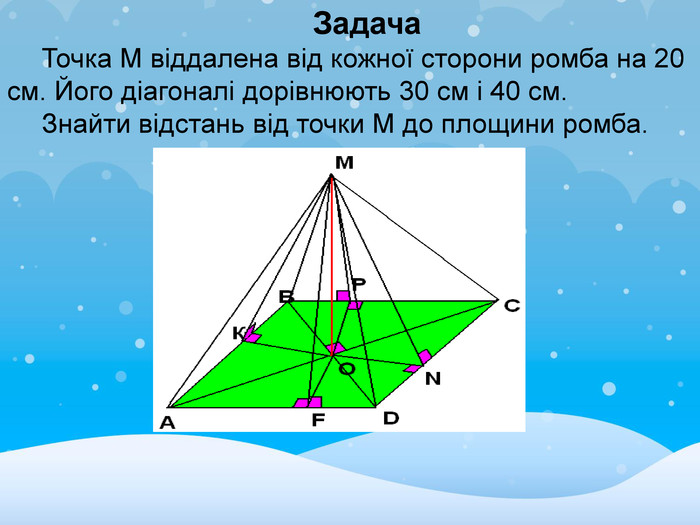
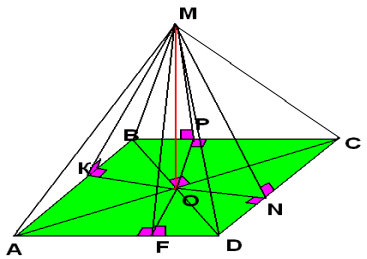
Задача

Точка М віддалена від кожної сторони ромба на 20 см. Його діагоналі дорівнюють 30 см і 40 см. Знайти відстань від точки М до площини ромба.

  В повсякденному житті ми доволі часто зустрічаємо перпендикуляри і похилі до площини. Це вежі, стовпи, телевізійні вишки та антени, щогли вітрильників і троси відтяжки.

  У професії «манікюрник», яку ми здобуваємо, також можна зустріти перпендикуляри та похилі. При обрізанні кутикул манікюрні ножиці приставляють перпендикулярно тій зоні, яку необхідно обробити. Пензлик під час нанесення лаку тримаємо під кутом 30˚. В даному випадку пензлик – це похила до площини нігтьової пластини.

1. Із точки В, що лежить на відстані 13,4 м від основи Львівської телевізійної вежі, її видно під кутом 86о. Визначити висоту вежі.

2. Над квадратною будівлею розміром 8 м на 8 м потрібно виготовити дах, найвища точка якого знаходиться на висоті 2 м над основою даху. Які найдовші крокви для цього потрібні?

( на практиці додають 30 см, щоб не затікало.)

Говерла – найвища вершина Українських Карпат і найвища точка України, висота 2061 м. Назва походить із румунської howirla —

«важкопрохідне підняття». Розташована в гірському масиві Чорногора, на межі

Надвірнянського району Івано-Франківської області та Рахівського району

Закарпатської області. Перший туристичний маршрут зі сходження на вершину

був відкритий у 1880 році.

3. До вершини гори Говерли ведуть дві дороги ВА і ВК, різниця довжин яких дорівнює 2 км. Знайти довжину доріг АВ та ВК, якщо їх проекції дорівнюють 5 км та 9 км.

      А зараз ми розв’яжемо задачу, в якій використовується одиниця вимірювання довжини фут. У світі з мір довжини, пов’язаних з людською ступнею, зберігся фут (англ., ступня): 1 фут = 0,3048 м = 30,48 см. 1 фут = 12 дюймів; 1 дюйм = 2,54 см.

4. Задача індійського математика XII ст. Бхаскари

На березі річки тополя росла.

І вітру порив її стовбур зламав.

Тополя упала і стовбур її

Кут прямий з течією ріки утворив.

Пам’ятай, в тому місці ріка

Чотири фути була шириною.

Верхівка схилилась до краю,

Залишивши три фути всього над водою.

Прошу, тепер швидше скажи мені ти:

Тополя якої була висоти?

5. Канатна дорога піднімає лижника зі швидкістю 2 м/с на вершину гори від її підніжжя за 15 хв. Визначити висоту гори, вважаючи, що кут нахилу гори наближено дорівнює 30˚.(додаткова задача)

Підсумок уроку

“На сьогоднішньому уроці ми застосували…”

“На початку уроку я поставив перед собою мету. Ось як я її досягнув…”

Домашнє завдання

   Підготуватись до к.р., №10.24, для учнів з високим рівнем знань № 10.27

   Я хочу, щоб наш девіз уроку став вашим гаслом і ви зрозуміли, що саме шлях міркувань – це найблагородніший шлях, а найважчий шлях є шлях власного досвіду. Але тіште себе висловом О. Суворова «Важко в навчанні, зате легко в бою».

Рівень А

     З точки до площини проведено дві похилі, які дорівнюють 5 см і 4 см. Проекція однієї з цих похилих на 5 см більша за проекцію другої похилої. Знайдіть відстань від цієї точки до площини.

Рівень Б

З точки до площини проведено перпендикуляр та дві похилі, які

дорівнюють 10 см і 17 см, а їх проекції відносяться, як 2:5. Знайдіть довжину перпендикуляра.

Рівень В

Через вершину прямого кута прямокутного трикутника проведено площину на відстані 4 м до гіпотенузи, яка паралельна цій площині. Проекції катетів на цю площину дорівнюють 12 м і 20 м. Знайдіть гіпотенузу.

Рівень А

     З точки до площини проведено дві похилі, які дорівнюють 5 см і 4 см. Проекція однієї з цих похилих на 5 см більша за проекцію другої похилої. Знайдіть відстань від цієї точки до площини.

Рівень Б

З точки до площини проведено перпендикуляр та дві похилі, які

дорівнюють 10 см і 17 см, а їх проекції відносяться, як 2:5. Знайдіть довжину перпендикуляра.

Рівень В

Через вершину прямого кута прямокутного трикутника проведено площину на відстані 4 м до гіпотенузи, яка паралельна цій площині. Проекції катетів на цю площину дорівнюють 12 м і 20 м. Знайдіть гіпотенузу.

Рівень А

     З точки до площини проведено дві похилі, які дорівнюють 5 см і 4 см. Проекція однієї з цих похилих на 5 см більша за проекцію другої похилої. Знайдіть відстань від цієї точки до площини.

Рівень Б

З точки до площини проведено перпендикуляр та дві похилі, які

дорівнюють 10 см і 17 см, а їх проекції відносяться, як 2:5. Знайдіть довжину перпендикуляра.

Рівень В

Через вершину прямого кута прямокутного трикутника проведено площину на відстані 4 м до гіпотенузи, яка паралельна цій площині. Проекції катетів на цю площину дорівнюють 12 м і 20 м. Знайдіть гіпотенузу.

Група А

Група Б

Група В