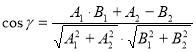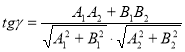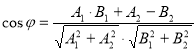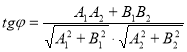Тест "Тестові завдання з математика"
Тестові завдання
з вищої математики
Варіант № 1
Питання 1: Яка система лінійних алгебраїчних рівнянь називається однорідною?
|
А |
Система, у якої головний визначник дорівнює 0 |
|
Б |
Система, у якої всі вільні члени дорівнюють 0 |
|
В |
Система, у якої головний визначник не дорівнює 0 |
|
Г |
Система, у якої всі вільні члени не дорівнюють 0 |
Питання 2: Коли операція множення матриць Аmxn та Вsxr неможлива?
|
А |
Якщо n=s |
|
Б |
Якщо m=s |
|
В |
Якщо n |
|
Г |
Якщо n |
Питання 3: Яка матриця А-1 називається оберненою до даної квадратної матриці А?
|
А |
Така, що А+А-1=Е, де Е- одинична матриця |
|
Б |
Така, що А·А-1=Е |
|
В |
Така, що А·Ат=А-1 де Ат- транспонована матриця |
Питання 4: Сума добутків елементів будь-якого рядка визначника на
алгебраїчні доповнення до елементів іншого рядка дорівнює:
|
А |
Значенню визначника |
|
Б |
Нулю |
|
В |
Одиниці |
Питання 5. Щоб розкрити невизначеність типу ![]() , утворену раціональними функціями, треба
, утворену раціональними функціями, треба
|
А |
Винести в чисельнику і знаменнику за дужки старший степінь змінної х. |
|
Б |
Чисельник і знаменник дробу помножити на вираз спряжений до ірраціонального |
|
В |
Чисельник і знаменник дробу розкласти на прості множники |
Питання 6. Який вигляд має рівняння прямої з кутовим коефіцієнтом?
|
А |
Ах + Ву + С = 0 |
В |
у - у0 = k( x - x0 ) |
|
Б |
у = kx + b |
Г |
|
Питання 7. Які умови паралельності та перпендикулярності двох прямих?
|
А |
|
B |
|
|
Б |
|
Г |
|
Питання 8. За якими формулами обчислюють кут між прямими?
|
А |
|
В |
|
|
Б |
|
Г |
|
Питання 9. Чому дорівнює площа паралелограма, побудованого на векторах ![]() ?
?
|
А |
|
В |
|
|
Б |
|
Г |
|
Питання 10. Яка умова колінеарності двох векторів ![]() та
та ![]()
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання 11. Дано вершини ΔАВС: А(-4;5),В(-1;17),С(5;9). Скласти рівняння висоти СD.
|
А |
4х + у – 31 = 0 |
Б |
х + 4у – 41 = 0 |
В |
|
Завдання 12. Написати рівняння еліпса, фокуси якого лежать на осі ОУ симетрично
відносно початку координат, якщо 2с=24, ![]() =
=![]() .
.
|
А |
|
Б |
|
В |
|
Завдання 13. Знайти координати та модуль вектора ![]() , якщо
, якщо![]() .
.
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання 14. Чому дорівнює скалярний добуток векторів ![]() та
та ![]() .
.
|
А |
-5 |
В |
14 |
|
Б |
28 |
Г |
7 |
Завдання 15. При якому значенні m вектори ![]() та
та ![]() перпендикулярні?
перпендикулярні?
|
А |
m=3 |
В |
m=2 |
|
Б |
m=-17 |
Г |
m=0,5 |
Завдання 16. Знайти векторний добуток векторів ![]() та
та ![]() .
.
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання 17. Яке рівняння має пряма, що проходить через точки А(-1;3) та В(2;5)?
|
А |
х + 2у + 2 = 0 |
В |
5х + у – 11 = 0 |
|
Б |
у = -5х + 7 |
Г |
2х - 3у + 11 = 0 |
Завдання 18: Обчислити визначник 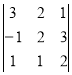
|
А |
2 |
Б |
0 |
В |
10 |
Г |
-1 |
Завдання 19. Знайти границю функції ![]()
|
А |
|
В |
|
|
Б |
|
Г |
0 |
Завдання 20. Розв’язати систему рівнянь матричним способом: 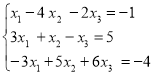
Варіант № 2
Питання 1. Яка система лінійних алгебраїчних рівнянь називається неоднорідною?
|
А |
Система, у якої головний визначник дорівнює 0 |
|
Б |
Система, у якої всі вільні члени дорівнюють 0 |
|
В |
Система, у якої головний визначник не дорівнює 0 |
|
Г |
Система, у якої хоча б один вільний член не дорівнює 0 |
Питання 2. Операції множення матриць Аmxn та Вsxr можлива?
|
А |
Якщо n=s |
В |
Якщо n |
|
Б |
Якщо m=s |
Г |
Якщо n |
Питання 3. Матриця А має обернену матрицю, якщо вона :
|
А |
Вироджена квадратна |
В |
Прямокутна, транспонована |
|
|
Б |
Невироджена квадратна |
Г |
Квадратна, транспонована |
|
Питання 4. Якщо ∆=0 і хоч один з визначників ∆1, ∆2, ∆3 не дорівнює нулю, то
система лінійних рівнянь:
|
А |
Має єдиний розв’язок |
|
Б |
Має безліч розв’язків |
|
В |
Не має жодного розв’язку |
Питання 5. Який вигляд має рівняння прямої, що проходить через точку
М0 (х0; у0) і має кутовий коефіцієнт?
|
А |
Ах + Ву + С = 0 |
В |
|
|
Б |
у = kx + b |
Г |
у - у0 = k( x - x0 ) |
Питання 6. Які умови паралельності та перпендикулярності двох прямих?
|
А |
|
B |
|
|
Б |
|
Г |
|
Питання 7. За якими формулами обчислюють кут між прямими?
|
А |
|
В |
|
|
Б |
|
Г |
|
Питання 8. Щоб розкрити невизначеність типу ![]() , утворену ірраціональними функціями
, утворену ірраціональними функціями
(або хоча б одна з них ірраціональна), треба
|
А |
Винести в чисельнику і знаменнику за дужки старший степінь змінної х. |
|
Б |
Чисельник і знаменник дробу помножити на вираз спряжений до ірраціонального |
|
В |
Чисельник і знаменник дробу розкласти на прості множники |
Питання 9. Чому дорівнює площа трикутника, побудованого на векторах ![]() ?
?
|
А |
|
В |
|
|
Б |
|
Г |
|
Питання 10. Якщо фокуси гіперболи лежать на осі ОУ, то її рівняння має вигляд?
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання 11. Обчислити визначник 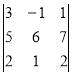
|
А |
2 |
Б |
0 |
В |
4 |
Г |
-1 |
Завдання 12. Яке рівняння має пряма, що проходить через точки А(2;-3) та В(1;4)?
|
А |
х + 2у + 1 = 0 |
В |
5х + у – 11 = 0 |
|
Б |
у = 11 – 7х |
Д |
7х - 3у + 11 = 0 |
Завдання 13. Дано вершини трикутника АВС: А(-4;5), В(-1;17), С(5;9). Скласти рівняння
прямої СК, паралельної стороні АВ.
|
А |
4х + у – 29 = 0 |
Б |
4х - у – 11 = 0 |
В |
|
Завдання 14. Написати рівняння еліпса, фокуси якого лежать на осі ОХ симетрично
відносно початку координат, якщо с=5, ![]() =0,6.
=0,6.
|
А |
|
Б |
|
В |
|
Завдання 15. Знайти рівняння асимптот гіперболи ![]() .
.
|
А |
у = |
Б |
у = |
В |
у = |
Завдання 16. Задано точки А (2;-1;2), В (3;2;1), С (-1;2;3). Знайти ![]() .
.
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання 17. Чому дорівнює скалярний добуток векторів ![]() та
та ![]() .
.
|
А |
-5 |
В |
14 |
|
Б |
11 |
Г |
9 |
Завдання18. При якому значенні m вектори ![]() та
та ![]() перпендикулярні?
перпендикулярні?
|
А |
m=3,5 |
В |
m=2 |
|
Б |
m=-17 |
Г |
m=0,5 |
Завдання 19. Знайти границю функції ![]()
|
А |
36 |
В |
18 |
|
Б |
1 |
Г |
0 |
Завдання 20. Знайти матрицю А-1, обернену до матриці А.
А=
Варіант № 3
Питання 1: Яка система лінійних алгебраїчних рівнянь називається однорідною?
|
А |
Система, у якої головний визначник не дорівнює 0 |
|
Б |
Система, у якої всі вільні члени дорівнюють 0 |
|
В |
Система, у якої головний визначник дорівнює 0 |
|
Г |
Система, у якої всі вільні члени не дорівнюють 0 |
Питання 2: Яка матриця А-1 називається оберненою до даної квадратної матриці А?
|
А |
Така, що А·А-1=Е |
|
Б |
Така, що А+А-1=Е, де Е- одинична матриця |
|
В |
Така, що А·Ат=А-1 де Ат- транспонована матриця |
Питання 3. Щоб розкрити невизначеність типу ![]() , утворену раціональними функціями, треба
, утворену раціональними функціями, треба
|
А |
Чисельник і знаменник дробу розкласти на прості множники |
|
Б |
Чисельник і знаменник дробу помножити на вираз спряжений до ірраціонального |
|
В |
Винести в чисельнику і знаменнику за дужки старший степінь змінної х. |
Питання 4. Які умови паралельності та перпендикулярності двох прямих?
|
А |
|
B |
|
|
Б |
|
Г |
|
Питання 5. Чому дорівнює площа паралелограма, побудованого на векторах ![]() ?
?
|
А |
|
В |
|
|
Б |
|
Г |
|
Питання 6. Операції множення матриць Аmxn та Вsxr можлива?
|
А |
Якщо m=s |
В |
Якщо n |
|
Б |
Якщо n=s |
Г |
Якщо n |
Питання 7. Якщо ∆=0 і хоч один з визначників ∆1, ∆2, ∆3 не дорівнює нулю, то
система лінійних рівнянь:
|
А |
Має єдиний розв’язок |
|
Б |
Не має жодного розв’язку |
|
В |
Має безліч розв’язків |
Питання 8. Які умови паралельності та перпендикулярності двох прямих?
|
А |
|
B |
|
|
Б |
|
Г |
|
Питання 9. Який вигляд має рівняння прямої з кутовим коефіцієнтом?
|
А |
Ах + Ву + С = 0 |
В |
у = kx + b |
|
Б |
у - у0 = k( x - x0 ) |
Г |
|
Питання 10. Якщо фокуси гіперболи лежать на осі ОХ, то її рівняння має вигляд?
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання11. Знайти координати та модуль вектора ![]() , якщо
, якщо![]() .
.
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання 12. Задано точки А (2;-1;2), В (3;2;1), С (-1;2;3). Знайти ![]() .
.
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання 13. Дано вершини ΔАВС: А(-4;5),В(-1;17),С(5;9). Скласти рівняння висоти СD.
|
А |
|
Б |
х + 4у – 41 = 0 |
В |
4х + у – 31 = 0 |
Завдання 14. Написати рівняння еліпса, фокуси якого лежать на осі ОУ симетрично
відносно початку координат, якщо 2с=24, ![]() =
=![]() .
.
|
А |
|
Б |
|
В |
|
Завдання 15. Чому дорівнює скалярний добуток векторів ![]() та
та ![]() .
.
|
А |
28 |
В |
14 |
|
Б |
-5 |
Г |
7 |
Завдання 16: Обчислити визначник 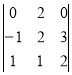
|
А |
10 |
Б |
0 |
В |
2 |
Г |
-1 |
Завдання 17. Знайти границю функції ![]()
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання18. При якому значенні m вектори ![]() та
та ![]() колінеарні?
колінеарні?
|
А |
m= -5; n= -7,5 |
В |
m=5; n= -7,5 |
|
Б |
m=3,5; n=5 |
Г |
m=0,5; n=5 |
Завдання 19. Яке рівняння має пряма, що проходить через точки А(1;3) та В(2;-5)?
|
А |
8х +у - 11 = 0 |
В |
у = -5х + 7 |
|
Б |
5х + у – 11 = 0 |
Г |
х + 2у + 2 = 0 |
Завдання 20. Розв’язати систему рівнянь: 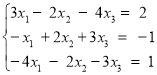
Варіант № 4
Питання 1. Яка система лінійних алгебраїчних рівнянь називається неоднорідною?
|
А |
Система, у якої хоча б один вільний член не дорівнює 0 |
|
Б |
Система, у якої всі вільні члени дорівнюють 0 |
|
В |
Система, у якої головний визначник не дорівнює 0 |
|
Г |
Система, у якої головний визначник дорівнює 0 |
Питання 2. Операції множення матриць Аmxn та Вsxr можлива?
|
А |
Якщо n |
В |
Якщо n=s |
|
Б |
Якщо m=s |
Г |
Якщо n |
Питання 3. Матриця А має обернену матрицю, якщо вона :
|
А |
Квадратна, транспонована |
В |
Прямокутна, транспонована |
|
|
Б |
Невироджена квадратна |
Г |
Вироджена квадратна |
|
Питання 4. Якщо ∆=0 і хоч один з визначників ∆1, ∆2, ∆3 не дорівнює нулю, то
система лінійних рівнянь:
|
А |
Має безліч розв’язків |
|
Б |
Має єдиний розв’язок |
|
В |
Не має жодного розв’язку |
Питання 5. Який вигляд має рівняння прямої, що проходить через точку
М0 (х0; у0) і має кутовий коефіцієнт?
|
А |
Ах + Ву + С = 0 |
В |
|
|
Б |
у = kx + b |
Г |
у - у0 = k( x - x0 ) |
Питання 6. Який вигляд має рівняння прямої з кутовим коефіцієнтом?
|
А |
|
В |
у - у0 = k( x - x0 ) |
|
Б |
у = kx + b |
Г |
Ах + Ву + С = 0 |
Питання 7. Які умови паралельності та перпендикулярності двох прямих?
|
А |
|
B |
|
|
Б |
|
Г |
|
Питання 8. За якими формулами обчислюють кут між прямими?
|
А |
|
В |
|
|
Б |
|
Г |
|
Питання 9. Чому дорівнює площа паралелограма, побудованого на векторах ![]() ?
?
|
А |
|
В |
|
|
Б |
|
Г |
|
Питання 10. Яка умова колінеарності двох векторів ![]() та
та ![]()
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання 11. Обчислити визначник 
|
А |
-1 |
Б |
0 |
В |
4 |
Г |
2 |
Завдання 12. Яке рівняння має пряма, що проходить через точки А(-2;-3) та В(1;4)?
|
А |
х + 2у + 1 = 0 |
В |
7х - 3у + 5 = 0 |
|
Б |
у = 11 – 7х |
Д |
5х + у – 11 = 0 |
Завдання 13. Дано вершини трикутника АВС: А(-4;5), В(-1;17), С(5;9). Скласти рівняння
прямої СК, паралельної стороні АВ.
|
А |
4х - у – 11 = 0 |
Б |
4х + у – 29 = 0 |
В |
|
Завдання 14. Написати рівняння еліпса, фокуси якого лежать на осі ОХ симетрично
відносно початку координат, якщо с=5, ![]() =0,6.
=0,6.
|
А |
|
Б |
|
В |
|
Завдання 15. Знайти рівняння асимптот гіперболи ![]() .
.
|
А |
у = |
Б |
у = |
В |
у =
|
Завдання 16. Знайти векторний добуток векторів ![]() та
та ![]() .
.
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання 17. Знайти координати та модуль вектора ![]() , якщо
, якщо![]() .
.
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання 18. Чому дорівнює скалярний добуток векторів ![]() та
та ![]() .
.
|
А |
-5 |
В |
14 |
|
Б |
7 |
Г |
28 |
Завдання 19. Знайти границю функції ![]()
|
А |
|
В |
0 |
|
Б |
2 |
Г |
-2 |
Завдання 20. Знайти матрицю А-1, обернену до матриці А.
А=
Варіант № 5
Питання 1: Коли операція множення матриць Аmxn та Вsxr неможлива?
|
А |
Якщо n=s |
|
Б |
Якщо m=s |
|
В |
Якщо n |
|
Г |
Якщо n |
Питання 2: Яка матриця А-1 називається оберненою до даної квадратної матриці А?
|
А |
Така, що А+А-1=Е, де Е- одинична матриця |
|
Б |
Така, що А·А-1=Е |
|
В |
Така, що А·Ат=А-1 де Ат- транспонована матриця |
Питання 3: Сума добутків елементів будь-якого рядка визначника на
алгебраїчні доповнення до елементів іншого рядка дорівнює:
|
А |
Значенню визначника |
|
Б |
Нулю |
|
В |
Одиниці |
Питання 4: Яка система лінійних алгебраїчних рівнянь називається однорідною?
|
А |
Система, у якої головний визначник дорівнює 0 |
|
Б |
Система, у якої всі вільні члени дорівнюють 0 |
|
В |
Система, у якої головний визначник не дорівнює 0 |
|
Г |
Система, у якої всі вільні члени не дорівнюють 0 |
Питання 5. Який вигляд має рівняння прямої з кутовим коефіцієнтом?
|
А |
Ах + Ву + С = 0 |
В |
у - у0 = k( x - x0 ) |
|
Б |
у = kx + b |
Г |
|
Питання 6. Які умови паралельності та перпендикулярності двох прямих?
|
А |
|
B |
|
|
Б |
|
Г |
|
Питання 7. За якими формулами обчислюють кут між прямими?
|
А |
|
В |
|
|
Б |
|
Г |
|
Питання 8. Щоб розкрити невизначеність типу ![]() , утворену раціональними функціями, треба
, утворену раціональними функціями, треба
|
А |
Винести в чисельнику і знаменнику за дужки старший степінь змінної х. |
|
Б |
Чисельник і знаменник дробу помножити на вираз спряжений до ірраціонального |
|
В |
Чисельник і знаменник дробу розкласти на прості множники |
Питання 9. Чому дорівнює площа паралелограма, побудованого на векторах ![]() ?
?
|
А |
|
В |
|
|
Б |
|
Г |
|
Питання 10. Яка умова колінеарності двох векторів ![]() та
та ![]()
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання 11. Дано вершини ΔАВС: А(-4;5),В(-1;17),С(5;9). Скласти рівняння висоти СD.
|
А |
4х + у – 31 = 0 |
Б |
х + 4у – 41 = 0 |
В |
|
Завдання 12. Написати рівняння еліпса, фокуси якого лежать на осі ОУ симетрично
відносно початку координат, якщо 2с=24, ![]() =
=![]() .
.
|
А |
|
Б |
|
В |
|
Завдання 13. Знайти координати та модуль вектора ![]() , якщо
, якщо![]() .
.
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання 14. Чому дорівнює скалярний добуток векторів ![]() та
та ![]() .
.
|
А |
-5 |
В |
7 |
|
Б |
28 |
Г |
14 |
Завдання 15. При якому значенні m вектори ![]() та
та ![]() перпендикулярні?
перпендикулярні?
|
А |
m=3 |
В |
m=0,5 |
|
Б |
m=-17 |
Г |
m=2 |
Завдання 16. Знайти векторний добуток векторів ![]() та
та ![]() .
.
|
А |
|
В |
|
|
Б |
|
Г |
|
Завдання 17. Яке рівняння має пряма, що проходить через точки А(-2;3) та В(2;7)?
|
А |
х - у + 5 = 0 |
В |
5х + у – 11 = 0 |
|
Б |
2х - 3у + 11 = 0 |
Г |
у = -5х + 7 |
Завдання 18: Обчислити визначник 
|
А |
2 |
Б |
0 |
В |
-1 |
Г |
10 |
Завдання 19. Знайти границю функції ![]()
|
А |
|
В |
|
|
Б |
0 |
Г |
|
Завдання 20. Розв’язати систему рівнянь матричним способом: 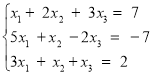


про публікацію авторської розробки
Додати розробку