Збірник тестів_ВСІ види рівнянь, нерівностей і іх систем (підготовка до НМТ з математики)
НМТ МАТЕМАТИКА
+відеорозбір
 Яснюк О.М.ВСІ
Яснюк О.М.ВСІ
види
рівняння,
нерівностей
і їх систем
які можуть Вам попастися на НМТ
Складу на 200!
Вітаю!
•  Мене звати Яснюк Олена Миколаївна
Мене звати Яснюк Олена Миколаївна
і я – вчитель математики
• Вже 18 рік допомагаю учням у вивчені математики, готую до НМТ/ЗНО
• Всі мої учні набирають бали, які їм
потрібні для вступу
• Багато учнів набрали 185+ балів
• З нуля за рік готую на 130-150 балів
• Закінчила Південноукраїнський національний педагогічний університет імені К.Д.Ушинського, вчитель математики
• Особистий результат ЗНО-2020 - 198 балів
Мій сайт: https://sites.google.com/view/olenayasniuk

ТГ-канал Складу на 200!
![]() @SkladuNa200
@SkladuNa200
Тести+теорія+новини
YouTube-канал Складу на 200!
![]() @SkladuNa200
@SkladuNa200
https://www.youtube.com/@SkladuNa200
Багато тестів, параметри
У збірнику Ви знайдете тестові завдання по всім видам рівнянь, нерівностей і їх систем, які Вам можуть трапитись на НМТ з математики. За допомогою цього збірника Ви можете продіагностувати себе, в кінці є відповіді до всіх завдань; підготуватися до НМТ за допомогою відео-розбору завдань; повторити ці теми перед НМТ.
Розв'язки завдань з повним поясненням Ви можете подивитися на моєму YouTube-каналі Складу на 200!: https://www.youtube.com/live/9n5FxKmjxe8?si=uv5vSRh_GD3NKKMa
У цьому відео-розборі не має тільки квадратичних нерівностей (завдання 1к,2к,3к). Як розв’язувати квадратичні нерівності можете пригадати за відео: https://youtu.be/HjD3pouCtEw?si=QJRK8J0Y3d3uG4qk
Список тем, які Ви можете повторити за допомогою цього збірника:
1. Лінійні рівняння
2. Основна властивість пропорції
3. Квадратні рівняння
4. Лінійні нерівності
5. Квадратичні нерівності
6. Дробові нерівності. Метод інтервалів
7. Системи нерівностей
8. Системи рівнянь
9. Рівняння і нерівності з модулем
10. Ірраціональні рівняння
11. Тригонометричні рівняння
12. Показникові рівняння і нерівності
13. Логарифмічні рівняння і нерівності
14. Додаткові завдання
Бажаю Вам успіхів у підготовці до НМТ з математики!
О.М.
Всі види рівнянь, нерівностей і їх систем
(Підготовка до НМТ з математики)
 1.
1.
2.
3.
4.
1к.
 2к. 3к.
2к. 3к.
5.
6.
7.
8.
9.
 10.
10.
11.
12.
13.
14.
15.
 16.
16.
17.
18.
19.
Додатково
 20.
20.
21.
22.
 23.
23.
24.
25.
26.
27.
Відповіді:
1 Б 8 Г 18 А 2 В 9 Д 19 Д 3 Б 10 А 20 Б 4 Г 11 Б 21 В 1к А 12 В 22 Д 2к Б 13 Д 23 Б
3к Д 14 В 24 А
5 Г 15 В 25 А
6 В 16 Д 26 Г
7 Г 17 Г 27 А
Список використаних джерел:
2. Боднар М.О. НМТ-2024. Завдання з математики, 2024
ДОВІДКОВІ МАТЕРІАЛИ
Таблиця квадратів від 10 до 49
|
Десятки |
|
|
|
|
Одиниці |
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
1 |
100 |
121 |
144 |
169 |
196 |
225 |
256 |
289 |
324 |
361 |
|
2 |
400 |
441 |
484 |
529 |
576 |
625 |
676 |
729 |
784 |
841 |
|
3 |
900 |
961 |
1024 |
1089 |
1156 |
1225 |
1296 |
1369 |
1444 |
1521 |
|
4 |
1600 |
1681 |
1764 |
1849 |
1936 |
2025 |
2116 |
2209 |
2304 |
2401 |
АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ
|
Формули скороченого множення |
|
Квадратне рівняння |
a2 – b2 = (a – b)(a + b) ax2 + bx + c = 0, a ≠ 0 (a + b)2 = a2 + 2ab + b2 D = b2 – 4ac – дискримінант
![]()
![]() (a – b)2 = a2 – 2ab + b2 x1 = —–b 2– a D , x2 = —–b 2+a D , якщо D > 0
(a – b)2 = a2 – 2ab + b2 x1 = —–b 2– a D , x2 = —–b 2+a D , якщо D > 0
|
Модуль числа |
–b— , якщо D = 0 x1 = x2 = 2а
a = ![]() a–a, якщо , якщо а а
a–a, якщо , якщо а а![]() < 0, 0 ax2 + bx + c = a(x – x1)(x – x2)
< 0, 0 ax2 + bx + c = a(x – x1)(x – x2)
|
тепені |
|
Логарифми |
|
|
a1 = а, аn = a ⋅ a ... ⋅ a для a ∈ R, n ∈ N, n n разів
1 a–n = —аn для а ≠ 0, n ∈ N
|
a > 0, а ≠ 1, b > 0, c > 0, k ≠ 0 alogab = b logаа = 1 logа1 = 0 logа(b ⋅ c) = logаb + logаc logа b–c = logаb – logаc logаbn = n ⋅ logаb |
||
(ab)x = ax ⋅ bx (a–b)x = —аbxx logаkb = ![]() аb
аb
|
Арифметична прогресія |
|
Геометрична прогресія |
a—1 + аn ⋅ n bn = b1 ⋅ qn – 1 Sn = b—1q (q– 1n– 1), (q ≠ 1) an = a1 + d(n – 1) Sn = 2
|
Теорія ймовірностей |
|
Комбінаторика |
P(A) = k–n Pn = 1 ⋅ 2 ⋅ 3 ⋅ ... ⋅ n = n! Cnk = k—! ⋅ (nn – ! k)! Ank = —(n – n!k)!
2
Похідна функції Первісна функції
та визначений інтеграл
, – сталі
|
|
Загальний вигляд |
|
Функція f(x) |
первісних F(x) + C, C – довільна стала |
|
0 |
C |
|
1 |
x + C |
|
x, ≠ –1 |
—x + 1 + C + 1 |
|
1–x |
ln x + C |
|
ex |
ex + C |
|
sin x |
–cos x + C |
|
cos x |
sin x + C |
|
—12 x cos |
tg x + C |
( )′ = 0
х′ = 1 (х)′ = x–1
![]() ( x)′ = –21x (ex)′ = ex
( x)′ = –21x (ex)′ = ex
(ln x)′ = 1–x (sin x)′ = cos x
(cos x)′ = –sin x (tg x)′ = cos–12x
(u + v)′ = u′ + v′ (u – v)′ = u′ – v′
(uv)′ = u′v + uv′ (Cu)′ = Cu′
(u–v)′ = u–′v – v2uv′
b b
∫f(x)dx = F(x)a = F(b) – F(a) – формула Ньютона-Лейбніца
a
Тригонометрія
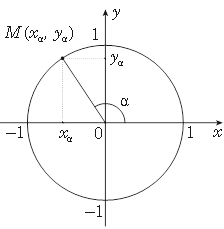 sin = y cos = x sin2 + cos2 = 1 tg = –cossin 1 + tg2 = cos–12 sin2 = 2sin cos cos2 = cos2 – sin2 sin(90o + ) = cos sin(180o – ) = sin cos(90o + ) = –sin cos(180o – ) = –cos tg(90o + ) = – –tg1 tg(180o – ) = –tg
sin = y cos = x sin2 + cos2 = 1 tg = –cossin 1 + tg2 = cos–12 sin2 = 2sin cos cos2 = cos2 – sin2 sin(90o + ) = cos sin(180o – ) = sin cos(90o + ) = –sin cos(180o – ) = –cos tg(90o + ) = – –tg1 tg(180o – ) = –tg
Таблиця значень тригонометричних функцій деяких кутів
|
α |
рад |
0 |
–π 6 |
–π 4 |
–π 3 |
–π 2 |
π |
3—π 2 |
2π |
|
град |
0o |
30o |
45o |
60o |
90o |
180o |
270o |
360o |
|
|
|
sin α |
0 |
1– 2 |
|
|
1 |
0 |
–1 |
0 |
|
|
cos α |
1 |
|
|
1– 2 |
0 |
–1 |
0 |
1 |
|
|
tg α |
0 |
|
1 |
|
не існує |
0 |
не існує |
0 |
23
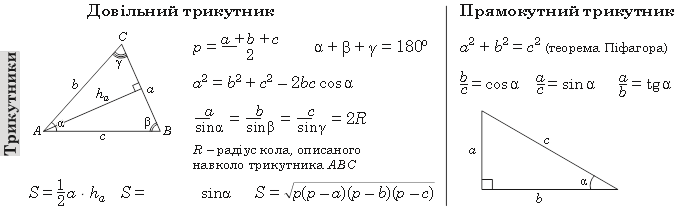
![]() ГЕОМЕТРІЯ
ГЕОМЕТРІЯ
Паралелограм Прямокутник
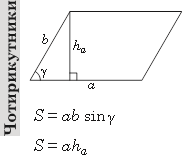 b
b  a
a
S= ab
 L = 2πR
L = 2πR
(x – x0)2 + (y – y0)2 = R2
Правильна піраміда
H 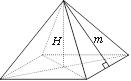
V = ![]() H
H
Sб = ![]() m
m
Координати та вектори
M(x0, y0, z0)
![]()
A(x1, y1, z1) B(x2, y2, z2)
Ромб Трапеція
|
|
a |
|
S = 1–2 d1d2, d1, d2 – діагоналі ромба |
S = —a + b2 ⋅ h, a і b – основи трапеції |

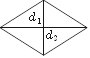 b
b
 S = πR2
S = πR2
|
Циліндр |
Конус |
Куля, сфера |

|
V = πR2H Sб = 2πRH |
V = 1–3 πR2H Sб = πRL |
V = 4–3 πR3 S = 4πR2 |
|
x0 = x—1 + x2 |
y0 = y—1 + y2 |
z0 = —z1 + z2 |
2 2 2

![]() AB(x2 – x1, y2 – y1, z2 – z1) AB= (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
AB(x2 – x1, y2 – y1, z2 – z1) AB= (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
![]()
a(a1, a2, a3) a ⋅ b = a1b1 + a2b2 + a3b3 φ b(b1, b2, b3) a ⋅ b = a⋅bcosφ
Кінець зошита
24



про публікацію авторської розробки
Додати розробку
