Підсумковий тест. Алгебра. 10 . 28.05.25

Тести Алгебра 10 клас Тест
Садрицька Г. П.
Додано: 15 квітня 2020
Предмет: Алгебра, 10 клас
Копія з тесту: Екстремальні значення
Тест виконано: 153 рази
Домашня робота
В реальному часі
Тестування
Відповідності
Флеш-картки
Роздрукувати
30 запитань
Запитання 1

Для функції, що зображено на рисунку знайдіть точки максимуму

варіанти відповідей

хmax= −3, xmax= 0, хmax= 3;  

хmax= 3

 xmax= 0,

хmax= −3,  хmax= 3;  

Запитання 2

Для функції, що зображено на рисунку знайдіть точки мінімуму.

варіанти відповідей

xmin= – 2; xmin= 3; xmin= 2

xmin= – 2; xmin= 3;

xmin= – 2; xmin= 2;

xmin=0

Запитання 3

За графіком функції, визначте критичні точки

варіанти відповідей

−3

0

3

4

3, 4

−4

Запитання 4

Знайдіть критичні точки функції f(x) = х2 – 4х.

варіанти відповідей

0 та 4

0

2

−2

Запитання 5

Знайдіть точки екстремуму функції  f(x) = х3 – 3х.

варіанти відповідей

0, 3, −3

−1

1

−1 та 1

Запитання 6

Знайдіть точку максимуму функції f(x) = х3 – 3х.

варіанти відповідей

0

1

−1

−1 та 1

Запитання 7

Скільки точок екстремуму має функції у = 2х3 −3х2 −12х.

варіанти відповідей

жодної

одну

дві

три

Запитання 8

Знайдіть точки екстремуму функції у = 2х3 −3х2 −12х.

варіанти відповідей

хmax = –1,

хmax = –1, xmin = 2; 

xmin = 2; 

хmax = 2, xmin = –1; 

Запитання 9

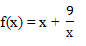
Знайдіть проміжки зростання  і точки екстремуму функції f(x)

 

варіанти відповідей

[− 3; 0) і ( 0; 3 ], xmin = − 3, xmax = 3

(− 3; 0 ), xmax = 3, xmin = 0

(− ∞; − 3] і [ 3; + ∞), xmax = − 3, xmin = 3

(− ∞; − 3] і [ 3; + ∞), xmax = 3, xmin = − 3

Запитання 10

Знайти екстремуми функції f(x)= x3 − 2x2 + 3


варіанти відповідей

уmax = 1, уmin = 3 ∕ 4

уmin = 0, уmax = 3 ∕ 4

Інша відповідь

уmax =3, уmin = 49 ∕ 27

Запитання 11

Установіть відповідність між функцією (1-4) та кількістю усіх точок екстремуму (А-Д) цієї функції.

1. у = 4х

2. у = 4х2 −1

3. у = х4 − 4х2

4. у = sin4x

А) безліч; Б) три; В) дві; Г) одна; Д) жодної.


варіанти відповідей

1Д; 2В; 3Б; 4А.

1Д; 2Г; 3Б; 4А.

1Д; 2В; 3Б; 4Г.

1Д; 2Г; 3В; 4А.

Запитання 12

Знайдіть проміжки зростання і спадання функції

f(x) = х3 + 3х2 − 9х


варіанти відповідей

Зростає на (-∞; -3] і [-1; +∞), спадає на [-3; -1]

Зростає на (-∞; -3] і [1; +∞), спадає на [-3; 1]

Зростає на (-∞; 9] і [-1; +∞), спадає на [9; -1]

Зростає на (-∞; -4] і [-1; +∞), спадає на [-4; -1 ]

Запитання 13

Знайти точки екстремуму функції у = х4 + 4х3 − 8х2 − 9


варіанти відповідей

хmin = −4; хmin = 1; хmax = 0

хmin = 4; хmin = −1; хmax = 0

хmax = −4; хmin = −1; хmax = 0

хmax = −4; хmin = 1; хmax = 0

Запитання 14

Чи має точки екстремуму функція у = 11?

варіанти відповідей

так

ні

неможливо визначити

безліч

Запитання 15

Знайдіть усі значення параметра а, при яких функція

у = −х3 + 3ах2 − 12х − 9 не має точок екстремуму.

варіанти відповідей

[−2; 2]

[−∞; −2]∪[2; +∞]

[−∞; −2]

[2; +∞]

Запитання 16

Знайдіть екстремуми функції у = 10√ ̅х̅ − х

варіанти відповідей

25

50

10√ ̅5̅ − 5

0

Запитання 17

Знайти проміжки зростання й спадання функції

f(x) = (x2 − 3) ∕ (x − 2)

варіанти відповідей

зростає на (−∞; 1] і [ 3; +∞), спадає на [1; 2) і ( 2; 3]

спадає на (−∞; 1] і [ 3; +∞), зростаєна [1; 2) і ( 2; 3]

зростає на (−∞; 1] і [ 3; +∞), спадає на [1; 3]

спадає на (−∞; 1] і [ 3; +∞), зростає на [1; 3]

Запитання 18

За якою схемою можна дослідити властивості функції для побудови її графіка?

варіанти відповідей

1. Знайти область значень функції.

2. Дослідити функцію на парність, непарність, періодичність (для тригонометрич-них функцій).

3. Знайти точки перетину графіка функції з осями координат.

4. Знайти похідну та критичні точки функції.

5. Знайти проміжки зростання, спадання та екстремуми функції.

6. Дослідити поведінку функції на кінцях проміжків області визначення, якщо це можливо.

7. За потреби знайти ще кілька точок графіка та використовуючи отримані результати, побудувати графік функції.

1. Знайти область визначення функції.

2. Дослідити функцію на парність, непарність, періодичність (для тригонометричних функцій).

3. Знайти точки перетину графіка функції з осями координат та проміжки знакосталості функції

4. Знайти похідну та критичні точки функції.

5. Знайти проміжки зростання, спадання та екстремуми функції.

6. Дослідити поведінку функції на кінцях проміжків області визначення, якщо це можливо.

7. За потреби знайти ще кілька точок графіка та використовуючи отримані результати, побудувати графік функції.

1. Знайти область визначення функції.

2. За потреби знайти ще кілька точок графіка та використовуючи отримані результати, побудувати графік функції.

3. Знайти точки перетину графіка функції з осями координат.

4. Знайти проміжки зростання, спадання та екстремуми функції.

5. Знайти похідну та критичні точки функції.

6. Дослідити поведінку функції на кінцях проміжків області визначення, якщо це можливо.

7. Дослідити функцію на парність, непарність, періодичність (для тригонометричних функцій).

1. Знайти похідну та критичні точки функції. Знайти область визначення функції.

2. Знайти точки перетину графіка функції з осями координат.

3. Дослідити функцію на парність, непарність, періодичність (для тригонометричних функцій).

4. Знайти область визначення функції.

5. Знайти проміжки зростання, спадання та екстремуми функції.

6. Дослідити поведінку функції на кінцях проміжків області визначення, якщо це можливо.

7. За потреби знайти ще кілька точок графіка та використовуючи отримані результати, побудувати графік функції

Запитання 19

1.   Знайдіть помилку у прикладі дослідження функції 

у = 9х2 (1− х)

1)     Область визначення D(у) = R

2)     Функція ні парна, ні непарна, неперіодична

3)     Точки перетину з осями координат:

х = 0; у = 0

у = 0; х1 = 0, х2 = 1

4)     Знайдемо інтервали спадання та зростання функції і точки екстремуму:

у’ = 18х − 27х2;  у’ = 0;

9х(2 + 3х) = 0;

х1 = 0, х2 = − 2 ∕ 3

 

варіанти відповідей

Помилку допущено у 1)

Помилку допущено у 4)

Помилку допущено у 3)

Помилку допущено у 2)

Запитання 20

Скільки критичних точок має функція f(x) = 3sin(x⁄3) − 1,5x


варіанти відповідей

Одну

Дві

Безліч

Жодної

Запитання 21

Знайдіть точку мінімуму функції f(x) = 4 + 3x⁸ − (x⁸) ∕ 4

варіанти відповідей

0

−3 і 3

4

інший варіант відповіді

Запитання 22

Дослідіть функцію у = 5х2 + 3х4 +π2 на парність


варіанти відповідей

парна

непарна

ні парна, ні непарна

неможливо визначити

Запитання 23

Задано функцію f(x) = x3 − 12x2 + 45x + 5 на проміжку [0;4]. В яких точках потрібно шукати максимальне і мінімальне значення цієї функції?


варіанти відповідей

0; 3; −4

0; 3; 4

0; 4

0; 3; 4; 5

Запитання 24

Знайти суму найбільшого і найменшого значення функції f(x) = x2 + 1 на проміжку [0;3].


варіанти відповідей

11

12

−12

0

Запитання 25

Знайдіть проміжки опуклості вниз функції у = cos2x + 6x2

варіанти відповідей

(−∞; +∞)

(−π ∕ 2; +∞)

(−∞; −π ∕ 2)

інша відповідь

Запитання 26

Установіть відповідність між функцією (1 - 4) і значенням другої похідної (А - Д) цієї функції в точці х0 = 1

1. у = х4 ∕ 4; 2. у = х3 − 2х2 ; 3. у = 1 ∕ (х − 2);

4. у = sin(3x − 3) ⁄ 3.

A) −3; Б) −2; В) 0; Г) 2; Д) 3 .

варіанти відповідей

1 − Б, 2 − В, 3 − А, 4 − Г

1 − Д, 2 − Г, 3 − Б, 4 − В

1 − Д, 2 − Б, 3 − Г, 4 − А

1 − А, 2 − Г, 3 − В, 4 − Д

Запитання 27

Тіло рухається прямолінійно за законом s(t) = t3 + t2 (s - у метрах, t - у секундах). Знайдіть прискорення тіла через 3 с після початку руху


варіанти відповідей

20 м/с2

33 м/с2

36 м/с2

14 м/с2

Запитання 28

Точка рухається прямолінійно за законом

s(t) = ¼ t4 − 2 t3 + 9 ⁄2 t2 + 2, де s вимірюється в метрах, t - у секундах. У який момент часу прискорення руху стане нульовим?


варіанти відповідей

t = 4 c

t = 2 c

t = √ ̅3̅ c

t = 3 c

t = 1 c

Запитання 29

Знайдіть точки перегину графіка функції у = х4 + 3х3 + 6х − 6


варіанти відповідей

−2

1,5

2

0

−1,5

Запитання 30

Знайдіть куб суми найбільшого і найменшого значення функції у = х3 – 12х + 7 на відрізку ⌈0;3⌉


варіанти відповідей

−2

−8

0

8

2

Створюйте онлайн-тести
для контролю знань і залучення учнів
до активної роботи у класі та вдома

Створити тест