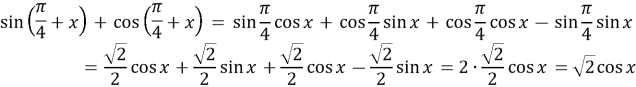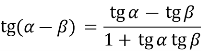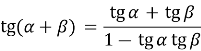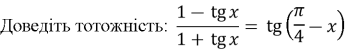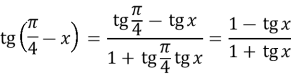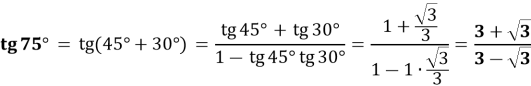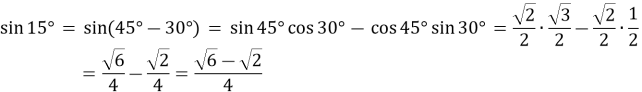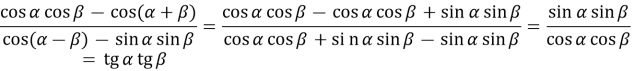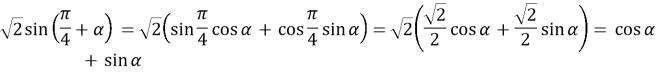Тригонометричні формули додавання
Тема: Тригонометричні формули додавання.
Мета:
- Навчальна: довести і засвоїти тригонометричні формули різниці і суми аргументів.
- Розвиваюча: навчити застосовувати тригонометричними формулами різниці і суми аргументів.
- Виховна: виховувати інтерес до вивчення точних наук;
Тип уроку: засвоєння нових знань;
Обладнання: конспект, презентація, мультимедійне обладнання;
Хід уроку
- Організаційний етап
- Привітання
- Перевірка присутніх на уроці
- Налаштування на роботу
- Актуалізація опорних знань
- Вивчення нового матеріалу
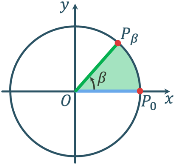
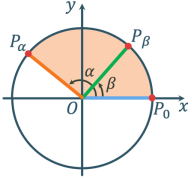
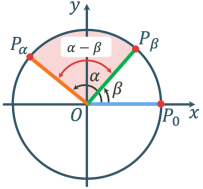
Косинус різниці і суми аргументів
|
|
Координати точки |
|
Координатами вектора |
|
|
|
|
Координати вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
||
|
Формули косинуса різниці і суми аргументів:
|
Приклад 1:
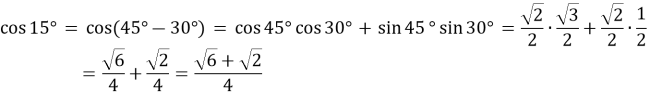
Синус різниці і суми аргументів
|
Формули синуса різниці і суми аргументів:
|
|
Приклад 2:
|
Тангенс різниці і суми аргументів
|
Формули тангенса різниці і суми аргументів:
|
|
Приклад 3:
*Для довдення тотожності, нам потрібно за допомогою тотожних перетворень показати, що ліва частина дорівнює правій, або навпаки. Покажемо в даному випадку, що ліва частина дорівнює правій, для цього до лівої частини застосуємо формулу тангенса різниці аргументів:
Отримали, що ліва частина дорівнює правій, тому тотожність доведено. Доведено. |
|
Приклад 4:
*Застосуємо формулу тангенса суми аргументів:
|
Говорячи про тригонометричні формули різниці і суми аргументів, слово «аргумент» можна не вживати, а казати просто «синус суми» чи «косинус різниці».
- Розв’язування завдань
№1
Обчисліть:
|
|
|
|
|
|
|
|
|
|
Розвʼязання:
|
|
|
||||||
|
|
|
||||||
|
|
|
||||||
|
Відповідь: |
1) |
|
2) |
|
3) |
|
|
№2
Спростіть вираз:
|
|
|
|
|
|
|
|
|
|
Розвʼязання:
|
|
|
||||||
|
|
|
||||||
|
|
|
||||||
|
Відповідь: |
1) |
|
2) |
|
3) |
|
|
- Підсумок уроку
- Які формули ми засвоїли сьогодні на уроці?
- Поясніть, як можна довести формулу косинуса різниці і суми?
- Поясніть, як можна довести формули синуса різниці і суми?
- Поясніть, як можна довести формули тангенса різниці і суми?
- Домашнє завдання
|
|
|
|
Опрацювати п.13 (стор. 76), вивчити формули Виконати № 13.2; 13.4; 13.8; 13.10; 13.12* |
А.Г. Мерзляк |
1


про публікацію авторської розробки
Додати розробку