Тригонометричні функції гострого кута прямокутного трикутника

Тема: Тригонометричні функції гострого кута прямокутного трикутника

Мета:

• домогтися засвоєння учнями змісту означень синуса, коси­нуса, тангенса і котангенса гострого кута прямокутного трикутника їх властивостей; сформува­ти вміння відтворювати зміст означень та їх властивостей, а також зна­ходити значення тригонометричних функцій гострого кута за даними прямокутного трикутника;
• розвивати математичні здібності усного рахунку, навички роботи за готовим рисунком;
• виховувати інтерес до вивчення геометрії.

Тип уроку: засвоєння нових знань.

Наочність та обладнання: конспект, картки з готовими рисунками.

Хід уроку

4. Формулювання мети і завдань уроку

В науці і техніці часто розв'язують задачі, в яких за відомими стороною і кутом прямокутного трикутника треба знайти невідомі його сторони і кути, або навпаки, знаючи сторони прямокутного трикутник, обчис­лити його кути. Прикладом таких задач є добре відомі вам задачі на засто­сування співвідношень між катетом, що лежить проти кута 30°, і гіпо­тенузою, рисунки до яких подані нижче (див. рис. 1).

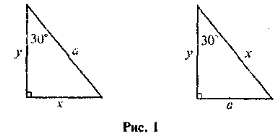Знайдіть х, у, якщо а — відоме.

Розв'язання цих задач демонструє залежність між довжиною катета, протилежним кутом 30° і довжиною гіпотенузи, тобто залежність між сторонами прямокутного трикутника та його кутом. Міркуючи послідовно, можна передбачити існування загальних залежностей між сторонами і кутами прямокутного трикутника, які можуть бути записані в алгебраїчному вигляді і одним з окремих випадків яких є відоме співвідношення між довжиною катета, протилежним кутом 30° і довжиною гіпотенузи. На сьогоднішньому уроці ми ознайомимося з означеннями синуса, косинуса і тангенса гострого кута прямокутного трикутника, які теж виражають відношення між сторонами цього трикутника. Мета уроку визначається як необхідність вивчення співвідношень між сторонами і кутами прямокутного трикутника та вивчення їх властивостей, а також опанування способів застосування цих співвідношень під час розв'язування задач.

Завданнями на сьогоднішній урок є:

• засвоїти зміст означень синуса, косинуса і тангенса гострого кута прямокутного трикутника;
• навчитися обчислювати синус, косинус, тангенс кута й будувати кут за його косинусом, синусом і тангенсом.

5. Засвоєння знань

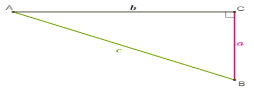
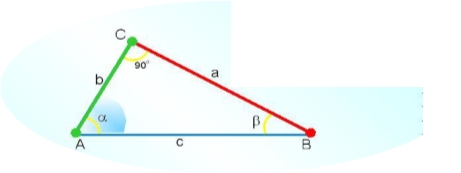
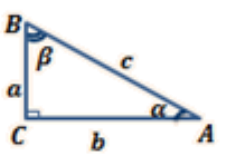
На рисунку зображено прямокутний трикутник ABC (). Нагадаємо, що катет BC називають протилежним куту A, а катет AC — прилеглим до цього кута.

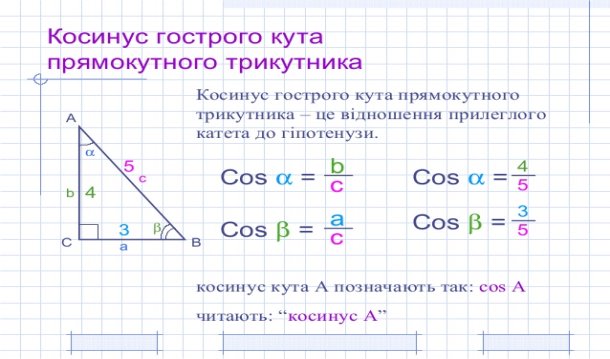
Для гострих кутів A і B прямокутного трикутника ABC маємо:

;   .

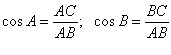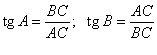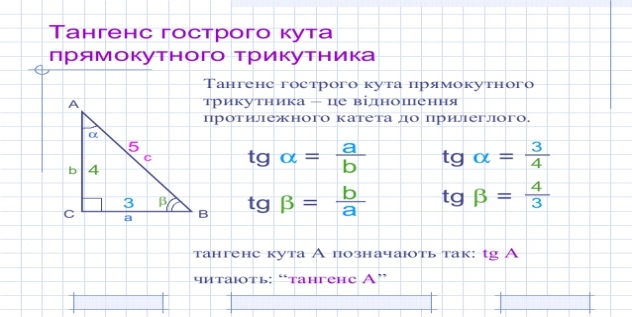
Давайте виразимо катети й гіпотенузу через sin a, sin β, cos a, cos β, tg a, tgβ.

a = c · sin a, a = c · cos β, b = c · cos a,

b = c · sin β, a = b · tg a, b = a · tg β, 

, , , , , .

Значення sinα , cosα  не може бути більше одиниці, тому, що катет завжди менший від гіпотенузи.

Значення tgα , сtgα  може бути і більше і менше одиниці, тому, що ці функції -  відношення катетів, які  мають різні значення.

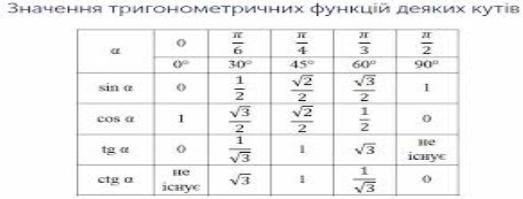
Дана таблиця є в підручнику, параграф 17

6. Формування первинних умінь

6.1 Виконання усних вправ

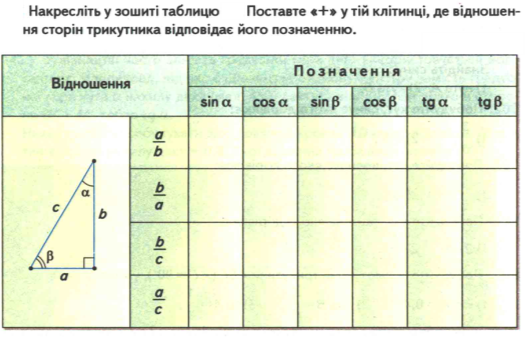
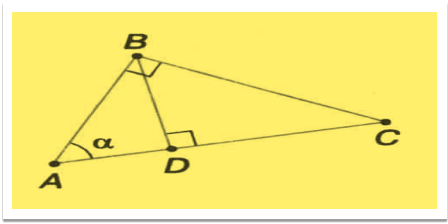Запишіть відношення sinα , cosα , tgα  через сторони

∆АВС і  ∆BDA

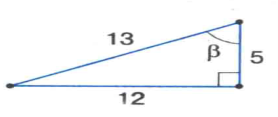
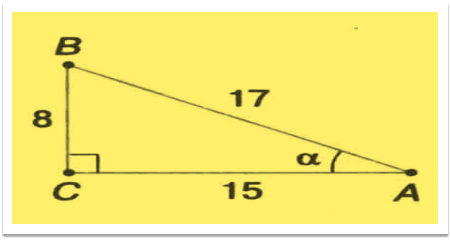За даними, наведеними на малюнку,  знайдіть

синус, косинус і тангенс кута α  з точністю до 0,1

6.3 Робота з підручником

Параграф 17, ст127. Розв’язати номери 579, 581

7. Підсумки уроку

    Запитання до класу

1. Що називають синусом, косинусом, тангенсом гострого кута а?
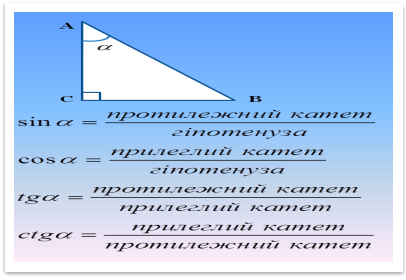2. Записати через назви сторін

Оцінювання учнів

8. Домашнє завдання

Опрацювати параграф 17, розв’язати 582