Творча робота: Історія виникнення чисел

                                     Творча робота на тему:

                «ІСТОРІЯ ВИНИКНЕННЯ ЧИСЕЛ»

Виконавець: учениця 6 класу загально освітньої школи І-ІІІ ступенів  № 123     

Палкіна Єлізавета

Керівник: вчитель математики                                                                                                Гончарова Наталія Петрівна

                                               Кривий Ріг - 2014

             Зміст

Введення                                                                                                           

Глава 1  .Походження слова «математика»

Глава  2    Числа та їх походження

Глава 3    Що таке натуральні числа                                                                           

Глава 4    Історія виникнення арифметики

Глава 5     Хто винайшов цифру нуль                                                                                               

Глава 6   Цифри у різних народів

Глава 7   Цікава історія походження назв цифр.

Глава 8   Геометрія і числа.

Висновок                                                                                                            

Список літератури                                                                                            

«Числа не управляют миром, но они показывают, как управляется мир».

Иоганн Гёте

                                                 Введення      

Виникнення чисел у житті не випадковість. Важко уявити собі спілкування без використання чисел. Історія чисел захоплююча й загадкова. Людство встановило низку законів і закономірностей світу чисел, розгадує  деякі таємниці та вживає свої відкриття у  повсякденні. Без чудовою науки про числа для  математики – немислимо сьогодні ні  минуле, ні майбутнє. А скільки ще нерозгаданого!    "Найдавніші з походження числа – натуральні. "Ручейки" натуральних чисел, зливаючись, породжують безмежний океан речовинних різного роду особливих спеціальних чисел", так писав про числахБ.А.Кордемский у своїй книжці "Дивний світ чисел".                                                                                                                               В сучасному світі людина постійно користується числами,не замислюючись про їх виникнення. Без знання минулого неможливо зрозуміти   сьогодення.                                          Тому метою моєї роботи є дослідження історії виникнення чисел,пов’язаною з необхідністю  вираження чисел знаками,знаходження зв’язку між геометричними фігурами та числами.                                                                                                                      Предметом мого дослідження є  історія виникнення чисел на прикладі натуральних чисел,дослідження прийомів  обліку у первиних людей,виникнення умовних знаків-цифр різних народів,зв'язок між геометрією та числами.                                                                                                                       Основними методи дослідження видів чисел є вивчення та обробка літературних джерел, систематизація даних.                                                                                    Завдання дослідження:                                                                                                                        1. Розглянути основні етапи розвитку натуральних чисел                                                                    2. Дослідити  прийоми  обліку у первиних людей                                                                   3.Установити залежність між виникненням чисел і необхідністю вираження цих  чисел  знаками                                                                                                                                                          4.. Геометричні фігури-це конкретне втілення чисел                                                                                                                        5. Розкрити таємничу магію і марновірство про деякі числа.                                            Актуальність дослідження зумовлена прагненням поглиблювати знання про оточуючий світі через дослідження історії виникнення чисел.

                  1.Походження слова «математика»

Слово «математика» виникло в Давній Греції приблизно в V столітті до н.е. Походить воно від слова «матема» -«навчання», «знання,  отримані через міркування»

         Давні греки знали чотири «матеми»:     

1.Вчення про числа (арифметика)

2.Теорія музики(гармонія)

3.Вчення про фігури и виміри(геометрія)

4.Астрономія и астрологія.

В старогрецькій науці існувало два напрямки. Представники першого із них, очолювані Піфагором, вважали знання призначені тільки для посвячених Ніхто не мав права ділитися своїми відкриттями зі сторонніми. Представники другого напрямку, навпаки, вважали, що математика відкрита для всіх хто здатен до продуктивних роздумів. Вони  називали себе математиками. Перемогу отримали представники другого напрямку.

                                 2.Числа та їх походження

Число — одне з найголовніших понять математики, яке в багатьох випадках може виступати як міра кількості чогось. У давнину у слов’янських мовах, слово «число» означало «знак», «символ», «поняття», «ідея» .                                                                                                  Під словом «числити» розуміли в ті часи «значити», «думати», а також «записувати щось за допомогою знаків», «робити певні дії зі знаками». Пізніше,зокрема з поширенням арифметики і точних наук на Русі Петром I y XVIII ст., під числами стали розуміти в першу чергу ті знаки,які використовуються для позначення певних кількостей. У XIX та XX ст., з розвитком та поширенням вищої, теоретичної математики, слово «число» знову починає вживатися більш широко-для  назви знаків, позначень і понять, які позначають не лише кількості – комплексні числа. Те саме ми спостерігаємо з поняттям «числити», «числення»- матричне числення, варіаційне числення .                                                                              Людині часто доводиться щось лічити: години, дні, гроші, роки тощо, тобто встановлювати кількість предметів, позначати її на письмі відповідними цифрами. Звідки взялися цифри? Як виникла лічба? Виявляється, потребу в цьому породило

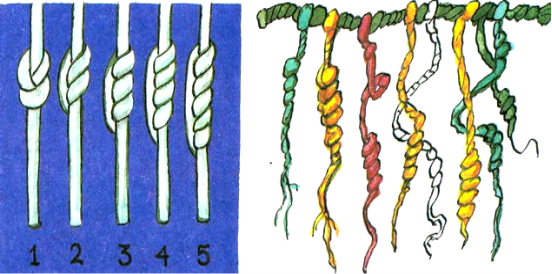
саме життя. Звичайно, первісна людина не користувалася такими словами: «один», «три», «чотири» тощо.                                                                                              

Для того щоб порахувати предмети, досить було показати їх на пальцях. Загнувши всі пальці на одній руці, переходили на другу. А коли пальців не вистачало, продовжували лічбу на тих же пальцях, але вже по другому колу. У сиву давнину люди рахували десятками. Вчені вважають, що Десяткова система числення (якою, до речі, користуємося і ми) пішла від десяти пальців на руках. Пальці були одночасно і лічильною машинкою. Щоб, наприклад, до п'яти додати два, достатньо загнути п'ять пальців на одній руці і два на другій. Загинаєш пальці — додаєш, розгинаєш — віднімаєш. Подекуди чинили інакше: якщо не вистачало пальців рук — переходили до ніг, тобто лічили двадцятками. Так, наприклад, лічили індійці майя, що жили на території сучасної Мексики та Гватемали. Інші люди рахували дюжинами — по 12. Напевно, тому, що число 12 має багато дільників, тобто його можна подати як дві шістки, три четвірки, чотири трійки і шість двійок. Шумери — мудрий стародавній народ, що займав територію між двома великими ріками Тигром і Євфратом — за основу лічби брали число 60. Більше ніж 5000 років тому вони запровадили великі числа, щоб вимірювати чималі урожаї, які вирощували навіть на посушливих ґрунтах. А щоб якось облікувати своє багатство, робили засічки: спочатку — на дереві, потім — на камені. З часом почали користуватися так званими блокнотами і зошитами. Виготовляли їх так: із сирої глини робили маленькі цеглинки, гострим предметом наносили на них потрібні позначки, а потім сушили (або випалювали). Коли глина висихала, помітки залишалися практично назавжди. Шістдесятковою системою лічби ми користуємося і сьогодні, коли обчислюємо, наприклад, час: у годині — 60 хвилин, у хвилині — 60 секунд.

Нумерація - це спосіб читання чи записування чисел.

0 1 2 3 4 5 6 7 8 9

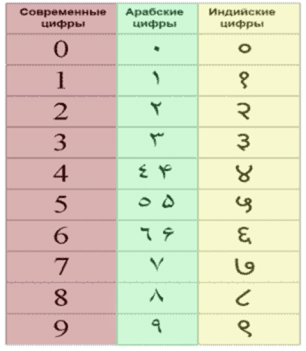
Ми з вами користуємося десятьма цифрами для запису будь-якого числа, отже,ми користуємося десятковою нумерацією.. Позиційна десяткова система числення була впроваджена в Індії. А вже з Індії ця система числення поширилась до інших країн. До нас позиційна десяткова система числення прийшла від арабів.                           Арабські цифри, як відомо, винайдено в Індії. Чому ж тоді вони називаються арабськими? Таку назву цифри  отримали тому, що набули значного поширення у світі взагалі та в Європі зокрема саме завдяки арабам. Навіть слово «цифра» арабського походження і означає «нуль». У нашій країні арабські цифри офіційно введені на початку XVIII століття, тобто разом із введенням громадянської азбуки. Цифру один зображували одною паличкою, два — двома, три — трьома, але лежачими. Чотири — це чотири палички, розміщені хрестоподібно, п'ять — це рука, кулак із відставленим пальцем. Якщо писати їх на папері швидко, накреслення цифр змінюється і нагадує сьогоднішнє:

                           3.Що таке натуральні числа

Дослівно - «природні» числа(лат. «natura» - природа). Існує вислів, що натуральні числа створені богом, а інші числа - витвір людської уяви. Натуральні числа – найдавніші числа,які стали використовувати люди, в першу чергу при лічбі:1,2, 3,… Сукупність всіх натуральних чисел позначається N. Число є одним з основних понять математики. Поняття числа розвивалося в тісному зв'язку з вивченням величин; цей зв'язок зберігається і тепер.  Існує велика кількість визначень поняття "число". Про числа перший почав міркувати Піфагор. Піфагору належить вислів "Всі чудово завдяки числу ". За його вченням число 2 означало гармонію, 5 - колір, 6 -Холод, 7 - розум, здоров'я, 8-любов і дружбу. А число 10 називали "священною четверіци ", так як 10 = 1 + 2 + 3 + 4. Воно вважалося священним числом і уособлювала весь Всесвіт.                                                                                                        Перше наукове визначення числа дав Евклід у своїх "Началах.": "Одиниця є то, відповідно, з чим кожна з існуючих речей називається однієї. Число є безліч, складене з одиниць ". Так визначав поняття числа і російський математик Магніцький у своїй "Арифметиці" (1703).                                                                Вважається, що термін "натуральне число" вперше застосував римський державний діяч, філософ, автор праць з математики та теорії музики Боецій (480 - 524 рр..), але ще грецький математик Нікомах з Герази говорив про натуральний, тобто природний  ряд  чисел.                                                                                              

Поняттям «натуральне число "в сучасному його розумінні постійно  користувався видатний французький математик, філософ-просвітитель Даламбер (1717-1783 рр..).                                                                                                                                  Початкові уявлення про числі з'явилися в епоху кам'яного століття, при переході від простого збирання їжі до її активного виробництва, приблизно 100 століть до н. е.. Числові терміни важко зароджувалися і повільно входили у вживання. Стародавній людині було далеко до абстрактного мислення, вистачило того, що він придумав числа: "один" і "два". Решта кількості для нього залишалися невизначеними і об'єднувалися в понятті "багато". Зростало виробництво їжі, додавалися об’єкти, які було потрібно враховувати в повсякденному житті, у зв'язку, з чим придумувалися нові числа: "три", "чотири" ... Довгий час межею пізнання було число "сім". Про незрозуміле говорили, що ця книжка "за сімома печатками", знахарки в казках давали хворому "сім вузликів з лікарськими травами, які треба було настоти  на семи водах протягом семи днів і приймати щодня по сім ложок ".

                                                                                                                                  Пізнаваний світ ускладнювався, були потрібні нові числа. Так дійшли до нової межі. Їм стало число 40. Надмірні кількості моделювалися величезним на той час числом "сорок сороків", рівним 1600.                                                                                     Великий інтерес викликає історія числа "шістдесят", яке часто фігурує в вавилонських, перських і грецьких легендах як синонім великого числа. Вавилоняни вважали його Божим числом: шістдесят ліктів у висоту мав золотий ідол з храму вавилонського царя Навуходоносора. Пізніше з тим же самим значенням (Незліченну безліч) виникли числа, кратні 60: 300, 360. З часом число 60 у Вавилоні лягло в основу шестидесятеричной системи обчислення, сліди якої збереглися до наших днів при вимірі часу і кутів.                                                                                         Наступним межею у слов'янського народу було число "тьма", (у древніх греків - мириада), рівне 10 000, а Запределье - "тьма тьмуща", рівне 100 мільйонам. У слов'ян застосовували також і іншу систему числення (так зване "велике число "або" великий рахунок ").                                                                                                          Таким чином, бачимо дивний парадокс: з одного боку, у сиву давнину були люди, які відчували потребу у лічбі, а також необхідність зафіксувати пораховане; а з іншого — на віддалених територіях понині живуть племена, які з метою лічби використовують лише слова «один» і «багато» або «один» і «два». Ось як, наприклад, рахують папуаси. Щоб вказати на один предмет, використовують слово «сакад», на два — «іна». Числівник «три» позначається словами «сакад-іна» (тобто один і два); «чотири» — «іна-іна» (два і два). Числа, більші від двадцяти, позначають словом «багато». Дещо незвично ведуть лічбу деякі племена у південній Африці. Для того, наприклад, щоб полічити биків (якщо їх кількість дорівнює трицифровому числу), потрібно троє людей. Після кожного бика, що проходить мимо них, загинає палець перший чоловік. Як тільки він загне всі десять пальців, одразу ж загинає один палець другий чоловік, вказуючи таким чином на кількість десятків. Коли ж і в нього не вистачає пальців, у лічбу включається третя людина. Мешканці островів Тихого океану використовують із цією метою камінчики або шкаралупу кокосового горіха: маленькі — для десятків, великі — для сотень.

Перші цифри появилися приблизно тоді ж, коли і перші букви. Стародавні греки записували їх просто буквами: А — один, В — два тощо. Слов'яни довгий час цифри на письмі зображували буквами кириличного алфавіту. А коли треба було позначити велику кількість предметів, то використовували описові звороти. При потребі вживати числа з більшим кількісним виміром наші предки знаходили слова, які, на їхній погляд, вказували на нескінченність. Це — ворон («вічний птах») — означало «десять мільйонів»,   колода («гріб») — «сто мільйонів».                                                                                                                Довго і важко людство добирався до 1-го рівня узагальнення чисел. Сто століть знадобилося, щоб вибудувати ряд найкоротших натуральних чисел від одиниці до нескінченності: 1, 2, ... в€ћ. Натуральних тому, що ними позначалися реальні неподільні об'єкти: люди, тварини, речі ... Найважче було придумати нуль. Його придумали на багато століть пізніше, ніж інші цифри. Перша точно датована запис, в якій зустрічається знак нуля, відноситься до 876 р.

                           4.Історія виникнення арифметики

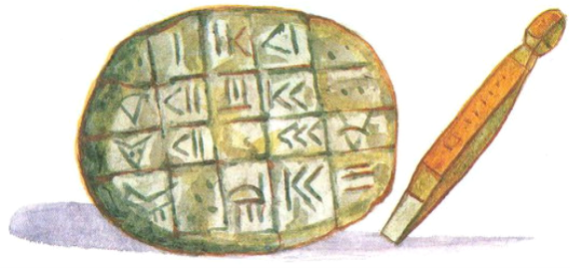
Історія арифметики охоплює період від виникнення рахування до формального означення чисел і арифметичних операцій над ними за допомогою системи аксіом. Арифметика — наука про числа, їх властивості і відношення — є однією з основних математичних наук. Вона тісно пов'язана з алгеброю і теорією чисел.Причиною виникнення арифметики стала практична потреба в рахуванні, найпростіших вимірюваннях і обчисленнях. Перші достовірні відомості про арифметичні знання виявлені в історичних пам'ятках Вавилона і Стародавнього Єгипту, які відносяться до III–II тисячоліть до н. е. Великий внесок у розвиток арифметики зробили грецькі математики, зокрема піфагорійці, які намагались за допомогою чисел визначити закономірності світу. У Середні віки основними сферами застосування арифметики були торгівля і наближені обчислення. Арифметика розвивалась в першу чергу в Індії та ісламських країнах, і тільки згодом прийшла до Західної Європи.                                                                 Вчені вважають, що історія виникнення чисел зародилася ще в доісторичні часи, коли людина навчилася рахувати предмети. Але знаки для позначення чисел з'явилися значно пізніше: їх винайшли шумери - народ, що жив в 3000-2000 рр. до н. е. у Месопотамії (нині в Іраку). Історія свідчить, що на табличках з глини вони видавлювали клиноподібні рисочки, а потім винайшли знаки. Деякі клинописні знаки позначали числа 1, 10, 100, тобто були цифрами, інші числа записувалися за допомогою з'єднання цих знаків. Користування цифрами полегшувало рахунок: рахували дні тижня, голови худоби, розміри земельних ділянок, обсяги врожаю. Користувалися цифрами і стародавні єгиптяни - про це свідчить математичний папірус Рінда, названий по імені англійського єгиптолога, який придбав його в 1858 р. в єгипетському місті Луксорі. На папірусі записані 84 математичні завдання з рішеннями. Судячи з цього історичного документу, єгиптяни користувалися такою системою цифр, в якій число позначалося сумою значень цифр.

                                              Стародавні числа в Індії

Наші первісні  уявлення про число й форму ставляться до дуже віддаленої епохи древнього кам'яного віку – палеоліту. У плині сотень тисячоліть цього періоду люди жили в печерах, в умовах, що мало відрізнялися від життя тварин,

Лише з настанням цього фундаментального перелому, перевороту, коли пасивне відношення людини до природи змінилося активним, ми вступаємо в новий кам'яний вік, у неоліт.

Самим важким етапом, що пройшло людство при виробленні поняття про число, вважається виділення ним поняття одиниці з поняття «багато». Воно відбулося, цілком ймовірно, ще тоді, коли людство перебувало на нижчому щаблі розвитку. В.В. Бобинін пояснює таке виділення тим, що людина звичайно захоплює рукою один предмет, а це, на його думку, і виділило одиницю із множини. Таким чином, початок числення Бобинін розглядає як створення системи, що складає із двох подань: одиниця й невизначена множина

Так, наприклад, плем'я ботокудов, що жило в Бразилії, виражало числа тільки словами «один» і «багато». Поява елемента «два» пояснюється виявленням можливості взяти по одному предметі в кожну руку. На первісному етапі рахунку людина зв'язувала це поняття з поняттям обох рук, у яких перебуває по одному предметі в кожній. При вираженні поняття «три» зустрілося утруднення: у людини немає третьої руки; це утруднення було переборено, коли людина догадалася поміщати третій предмет у своїх ніг. Таким чином, «три» характеризувалося підняттям обох рук і вказівкою на ноги. Звідси порівняно характерно відбулося виділення й поняття «чотири», тому що з одного боку, до цього спонукувало зіставлення двох рук і двох ніг, а з іншого боку - можливість помістити по одному предметі в кожної ноги. На першому щаблі розвитку рахунку людина ще аж ніяк не користувалася найменуванням чисел, а виражала їх або в ногах, або відповідними рухами тіла або жестами.

Подальший розвиток рахунку відноситься, імовірно, до тієї епохи, коли людство ознайомилося з деякими формами виробництва - полюванням і рибальством. Людині довелося виготовляти найпростіші знаряддя для оволодіння цими виробництвами. Крім того, просування людини в холодні країни змусило його робити одяг і створювати знаряддя для обробки шкіри.

Помалу зложилося первісно-комуністичне суспільство з відповідним розподілом їжі, одягу й знаряддя. Всі ці обставини змусили людину так чи інакше вести лік спільного майна, сил ворога, з яким доводилося вступати в боротьбу за оволодіння новими територіями. Процес рахунку вже не міг зупинитися на чотирьох і повинен був розвиватися далі й далі.

На цьому щаблі розвитку людина вже відмовляється від необхідності брати перелічувані предмети в руку або класти до ніг. У математику входить перша абстракція, що полягає в тім, що перелічувані предмети заміняються якими-небудь іншими однорідними між собою предметами або знаками: камінчиками, вузликами, гілками, карбами. Операція виробляється за принципом взаємо-однозначної відповідності: кожному перелічуваному предмету у відповідність один із предметів, обраних як знаряддя рахунку (тобто один камінчик, один вузлик на мотузці й т.д.). Сліди такого роду лічби збереглися в багатьох народів і дотепер. Іноді такі примітивні знаряддя рахунку (камінчики, раковини, кісточки) нанизували на шнурок або паличку, щоб не розгубити. Це згодом привело до створення більше зроблених рахункових приладів, що зберегли своє значення й до наших днів: російська рахівниця й подібний з нею китайський суан-пан.

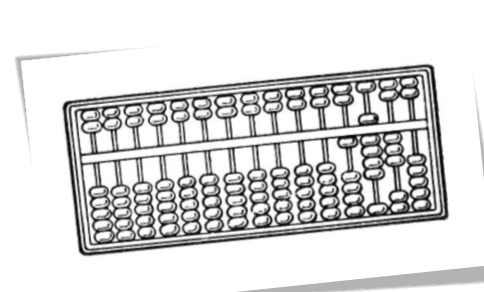
Суан-пан
 

                                   5.Хто винайшов цифру нуль

Поняття нуля з'явилося і здобуло сенс відносно недавно - лише в 5 столітті н.е. До цього моменту математики намагалися виконувати тільки найпростіші арифметичні розрахунки. Сьогодні нуль як символ (або цифра) - поняття, що означає відсутність будь-якої кількості, яке дозволяє нам виконувати розрахунки і вирішувати складні рівняння. Шістсот років потому математики народу майя використовували поняття «порожнечі», тобто нуля у своїх складних календарних розрахунках. Нуль для них служив в якості кордону між старим і новим циклом. Проте в рівняннях і підрахунках нуль як і раніше не використовувався.Деякі вчені впевнені, що індійські математики запозичили початкову концепцію нуля у вавилонян. Інші, навпаки, вважають, що індійський нуль, як число, розвивався самостійно. Вперше поняття нуля з'явилося в Індії приблизно на початку 5 століття н.е. Математичні рівняння були викладені у формі поезії або піснеспіви, але не позначалися символами. Такі слова як «порожнеча», «небо» або «простір» спочатку символізували нуль. А в 628 році індійський астроном і математик Брахмагупта уклав абстрактне поняття нуля в символ - крапка. Крім того, він розробив математичні операції з використанням цієї цифри, написав правила для досягнення нуля шляхом додавання і віднімання, а також оприлюднив результати використання нуля в рівняннях. Саме завдяки йому вперше нуль був визнаний не тільки як ідея, але і як число.Протягом кількох наступних століть поняття нуля як числа набуло популярності і в Китаї, і на Близькому Сході. І нуль став невід'ємною частиною арабської системи розрахунків, яка була заснована на індійській системі. Перський математик Мохаммед за допомогою нуля розробив методи швидкого множення і ділення чисел, які відомі як алгоритми. Трохи пізніше нуль проклав свій шлях і до Європи

• Нуль виник пізніше, ніж інші числа.
• В римській і єгипетській нумерації обходилися без нуля.
• В Європі користуються арабською(індійською нумерацією) де цифра нуль має велике значення.

                               6.Цифри у різних народів

                                             Стародавній Рим

У стародавніх римлян була своя система цифр. Так, наприклад, щоб записати один, два чи три, використовували палички — І, II, III. П'ять — це п'ять пальців руки. Щоб не малювати чотири пальці і один великий, зображували схематично так: V. Десять — це дві руки, тобто два рази по п'ять: X. Чотири — це від п'яти відняти один, тобто одиничку писали зліва від п'ятірки (IV), а шість — навпаки: VI (п'ять плюс один). Сім — це п'ять і два (VII), вісім — п'ять і три (VIII). Щоб записати число дев'ять, треба від десяти відняти один, тобто одну паличку записати перед десяткою (IX). А так зображували інші числа:

L — 50    С — 100                                                                                                                           D — 500    М — 1000

Цікаво, що римські цифри винайдені не самими римлянами, а їхніми попередниками — етрусками. Римляни запозичили ці зображення, вдосконалили. Від римлян цифри помандрували до інших народів Європи і використовувалися ними, аж поки на зміну їм не прийшли арабські цифри. Однак римські цифри абсолютно не зникли. І тепер часто ставлять їх на циферблатах годинників, ними позначають розділи книг, томи творів, порядкові номери конференцій,  фестивалів, спортивних ігор тощо.Римська система нумерації була мало пристосована для обчислень. Римські числові знаки виникли до появи алфавіту і не походять від його літер. Вважається, що спочатку числа від 1 до 9 позначались відповідною кількістю вертикальних рисочок, а їх перекреслення вказувало на збільшення числа вдесятеро (звідси число X). Відповідно, щоб отримати 100 рисочку перекреслювали два рази. У подальшому відбулось спрощення системи

                                             Стародавня Греція

На самому початку греки користувались аттичною нумерацією, яка використовувала знаки для чисел 1,5,10,50,100,500,1000. Цю систему описав граматик і історик Геродіан у II столітті н. е. За допомогою аттичної нумерації записувались результати обчислень на лічильній дошці абак. З часом аттичну нумерацію змінила компактна літерна — іонічна Іонічна нумерація використовувала 24 літери грецького алфавіту і три літери, що вийшли з обігу, для позначення одиниць від 1 до 9, десятків від 10 до 90 і сотень від 100 до 900 (літери, що вийшли з обігу використовувались для позначення чисел 6,90,900⁾Щоб відрізнити числа від літер над ними ставили риску. Для запису числа 1000 використовували той самий символ, що й для одиниці, але з рискою знизу ліворуч. Це нагадує позиційну систему, але остаточного переходу не відбулось.Вважається, що така система утруднювала складні обчислення, але у 1882 році французький історик математики Поль Таннері дійшов висновку, що за правильного підходу грецька система нумерації не сильно відрізняється від десяткової за швидкістю обрахунків.

                                                      Індія

Позиційна система числення (десять цифр, включаючи нуль) була введена в Індії. Вона дозволяла розробити відносно прості правила виконання арифметичних операцій. Учені вважають, що в Індії позиційна система вперше з'явилась не пізніше початку нашої ери. Однак через те, що індійці використовували крихкі матеріали для письма, документальних пам'яток цього не збереглось. Достеменним документом, що використовує позиційну систему нумерації вважається Бакхшалійський рукопис який датується XII століттям.Для цілих чисел в Індії використовувалась десяткова система. Спочатку це були цифри «карошті», які писались справа наліво, а потім «брахмі», які писались зліва направо. Обидва варіанти використовували адитивний принцип для чисел до 100 і мультиплікативний — далі. Однак в брахмі використовувались спеціальні знаки для чисел від 1 до 9. На основі цієї система були розроблені сучасні цифри «деванагарі» (чи божественне письмо), які почали застосовувались в десятковій позиційній системі. До 595 року належить перший запис числа, в якому застосовуються дев'ять цифр, нуля ще не було. Для зручності обчислень Аріабхата запропонував записувати цифри літерами санскриту.

            7.Цікава історія походження назв цифр.

Цікава історія походження назв деяких чисел. Учені, наприклад, вважають, що числівник п'ять походить від іменника «п'ясть» (рука), тобто трактується як «п'ять пальців п'ясті». Чи не найбільшою популярністю користується у людей число сім: сім днів у тижні, сім чудес світу; у казках — сім господинь, семеро козенят, сім сестер. У чому ж причина? Виявляється, що число сім відповідає обсягу короткотривалої пам'яті людини, тобто це та кількість предметів, ознак, яку ми спроможні запам'ятати відразу і на більш-менш тривалий час (кількість предметів для різних людей неоднакова: вона перебуває у межах 7 ± 2, тобто від 5 до 9 одиниць). Приблизно чотири тисячі років тому люди, які населяли територію сучасного Іраку, мали вже перші астрономічні відо­мості. На зоряному небі вони спостерігали рух п'яти планет, які разом із Землею і Сонцем утворювали систему із семи небесних тіл. Ще вони зауважили, що місяць має 28 діб; цю кількість поділили на чотири рівні частини, щоб кожен із семи одержаних днів присвятити одному з семи світил. Так утворився семиденний тиждень, який ми зараз маємо і який перейшов у такому ж складі й до інших народів.                                                  У Вавилоні довершеним вважалося і число дванадцять. Припускають, що навіть шістдесятерична система числення, якою користувалися вавилоняни, була пов'язана із числами п'ять (кількість пальців на руці) і дванадцять (кількість місяців року). Крім того, дванадцять має багато дільників: 2, 3, 4, 6. Наступне число — тринадцять — не ділиться ні на що-Побутує думка, що воно нещасливе, «чортова дюжина», тобто нічого доброго не віщує. У 1930 році в Англії декілька тисяч жителів Лондона підписали петицію, у якій висловили прохання до уряду зняти з будинків тринадцяті номери. А в США, наприклад, деякі високопоставлені службові особи ніколи не заходять у кімнати з таким номером. Однак не всі люди такі забобонні, а деякі бояться інших чисел (китайці, наприклад, вважають нещасливим число чотири). Цікавим є походження числівника сорок. Східнослов'янське слово «сорок» змінило поширене до нього загальнослов'янське слово «четыре десяте». Числівник сорок спочатку був іменником, який мав значення «мішок». Це справді був мішок, у який поміщалося рівно 40 шкірок соболів чи білок, бо саме стільки їх ішло на пошиття однієї шуби. Зашитий і запечатаний сорок із вказаною кількістю шкірок за часів Київської Русі служив грошовою одиницею.                                                                                                                                        Від слова «сорок» пішла назва «сорочка» (очевидно тому, що вона схожа на мішок). Число тисяча утворилося шляхом поєднання двох слів: «тук, тыти» (слов'янське), що означає «жир, жиріти», і слова «сет», пов'язаного з індоєвропейським позначенням сотні. Цим люди ніби хотіли підкреслити, що тисяча — це «товста сотня», «велике сто». Число десять тисяч стародавні слов'яни називали «тьми», тобто темне число, яке важко чітко уявити. Цікава історія виникнення числа мільйон. Коли венеційський купець XIII століття Марко Поло повернувся додому після 24-річних мандрів, він багато розповідав про ті місця, де побував. Згадуючи про Китай, купець намагався описати багатства, якими володів монгольський хан Хадилай. Із цією метою він до слова «мілле», що означало «тисяча», додав суфікс збільшення -он-е. І вийшло «мілліоне», тобто «величезна тисяча». А через деякий час це слово стало позначати «тисячу тисяч». Цікаво, що словам купця мало хто вірив, часто з нього насміхалися, називали «Мес-сер Марко Мільйон». Тільки після того, як багатства Китаю побачили інші купці, добре ім'я Марка Поло було реабілітоване. Число мільярд уживається з XIX ст. Деякий час для позначення цієї ж кількості використовувався й інший числівник — більйон, який зараз майже зовсім вийшов з ужитку. Що стосується нуля, то до нього люди додумались із великим зусиллям. Спочатку нуля не було зовсім. Для обчислень користувались дошкою, розлініяною у клітинки, і кружечками, на яких були написані цифри. Таку рамку називали абаком. Як бачимо, нуль просто пропускали. Іноді замість абака використовували звичайну дошку без клітинок. Тоді місце порожньої клітинки позначали кружечком (нічого, порожнє місце). А коли почали здійснювати обчислення на папері, порожній кружечок перетворився на нуль.

                      8.Геометрія і числа

Піфаго́р                                                                                                                                                  580 до н. е. — 500 до н. е.) —                                                                                 давньогрецький філософ

Іоганн Гёте казав: «Числа не управляют миром, но они показывают, как управляется мир» Геометричні фигури – це конкретне втілення  чисел: число 5 зв’язується  з пентаграмою, 4 - с квадратом, 3 – з трикутником, 2 – з линиею, 1 – з  точкою.                                                                                     .                                   В піфагорійській геометрії числа приміняли до простору.Елементи простіру  і геометричні фігури, вони зводили  до числа. Так, точка є просторова одиниця, лінія- просторова 2,поверхня- 3, тіло-4. В стереометрії  піфагорійці вперше відкрили 5 правильних геометричних тіл: куб, тетраедр,октаедр, ікосаедр і додекаедр. Піфагор перший  зробив геометрію  справжньої наукою.Священними числами важались одиниця,як початок  чисел,трійка,четвірка і сама десятка. Згодом містика  чисел у  піфагорійців сильно розвинулась. . " Всё есть число " стає універсальним методом їх наукових побудов.                                                                                                                                               У релігійній  традиції центральними є  три основні геометричні фігури:коло, трикутник та квадрат. Вважалося, що вони є три рівні нашого буття: дух, розум і тіло.З  геометрія було зв’язане  і  вивчення чисел. Ідеальними важалися  цілі числа — вони, здавалося закінченими.Дріби  як число в зародковому стані в Цілі числа  пізнавальні Оскільки  числа або раціональні, або ірраціональні, то геометрія може навести  мости між ними.. Квадрат і його діагональ. Наприклад, діагональ квадрата зі стороною,що дорівнює одній  одиниці, дорівнює квадратному  кореню із 2.Термін "корінь" у фразі «квадратний корінь» має давнє походження і  має поняття взяте із  природи. Корінь рослини  прихований, але живить те, що на поверхні. Так само, приховані і корені квадратних чисел, і всі вони знаходяться в  них. Наприклад, квадратний корінь  із 16 дорівнює 4 (4 х 4 = 16) а корінь квадратний із 15- ірраціональне число, що не так легко обчислити.Знаходження квадратних коренів було  основним заняттям стародавніх математиків. Коли квадратний корінь числа не можна  було обчислити  в цифрах ,то завжди можна було відтворивати геометрично. Цим і  пояснюється, влада геометрії  в стародавньому світі. Геометрії вважалась воротами в  вищі  сфери  свідомості, і тому її принципи були включені в релігійне мистецтво і архітектуру                                                                                                                                                 Про числа 25, 49, 100 говорять,що  вони є  квадратами,тому що вони отримані, якщо  піднести 5, 7 і 10 в квадрат. У стародавні часи часто                                                              обчислювали за допомогою каменців  і, звичайно, відмічали випадки, в яких можна скласти каменьці  у вигляді правильної фігури. Крім квадратних чисел були відомі трикутні числа. П'ятикутні  числа зображенні на малюнку. Щоб зобразити  п'ятикутне число, його необхідно розділити на три трикутні. а потім буде залишатися n точок, як показано на малюнку.                 Ви можете  представити число у вигляді прямокутника. Для числа 12 це  можна зробити  багатьма способами,а для числа13  тільки розставивши  всі елементи в одину лініюТаке . древні не  важали прямокутним.Таким чином,  прямокутними  числами є всі складені числа, а не прямокутними-прості  числа. До фігурних чисел  також відносяться пірамідальні числа,які одержуються, якщо шари  складати пірамідою, як раніше складали ядра перед пушкою..  Легко зрозуміти, що пірамідальне число дорівнює сумі всіх трикутних чисел, від першого до n го.

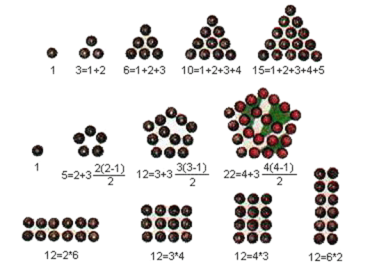
Монада 1 - не маюча параметров точка

Монада, 1 називається так тому, що вона завжди залишається в одному і тому ж стані, тобто  відокремлена від  множини, її атрибутами є наступне: вона називається розумом, оскільки розум є стабільним ; парною  і непарною, тому, що, будучи прибавленою до парного числа, дає непарне, а прибавлена до непарного числа, дає парне.; Богом, тому що це початок і кінець всього, але сама по собі не є ні початком  ні кінцем.; в часі вона  теперішнє,тому що вічність не знає, ни  минулого, ні майбутнього

Дуада 2 – відрізок,що з’єднує дві точки.

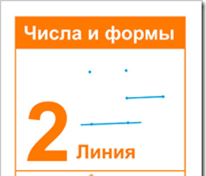
Дуаде, 2,були дані, тому що вона завжди розділена та представляє  два,а не один і вони протилежні один одному, наступні символічні імена : дух, зло темрява,  нестабільність. Монада є символом мудрості, Дуада –символом невігластва, тому що в ній є сенс поділу, який є початком невігластва.

внушительность, женитьба, душа и наука.                                                                                   .Піфагорійці почитали монаду и презирали дуаду, потому что вона символізує  полярність.

Триада 3 - треугольник, или  плоскость

Тріада, 3, –є  першим числом, що по-справжньому непарне (Монада не завжди розглядається як число). Це  перший баланс одиниць. Ключовими словами для Тріади  є: "дружба", "світ", "справедливость", "розсудливість", , "чесність." Це число називається мудростю, тому що люди представляють теперішнє, передбачають майбутнє і використовувують досвід минулого. Воно визиває мудрість і порозуміння. Триада є число пізнання музики,геометрії, астрономії і науки про небесні та земні  тіла.Символом триади є трикутник.

Тетрада 4 - тетраедр,або об’єм.

Тетрада, 4, розглядалась пифагорійцями,як корінь всіх речей, джерело  Природи і найбільш  досконале із чисел. Більше того, тетрада є середина  тижня, число  проміжне між 1 і 7. Тетрада є також перше  геометричне тіло.Пифагор стверджував, що Душа людини складається із тетради, при цьому чотири сили душі – це ум, наука,думки і почуття  Ключевыми словами до тетради є “стримкість”, “сила”, “мужність”, власник ключа до  Природи, потому що універсальна конституція не може існувати без тетрады. Вона також називаеться гармонією ,  первиною глибиною і важливістю.

Пентада

Пентада, 5,є  союз парного і непарного чисел (3 і 2). Серед греків пентаграма була священним символом світла, здоров'я і життєздатності.Вона також символізує  п'ятий елемент-ефір, тому що він вільний від впливу чотирьох . нижніх елементів. Вона називається балансом, оскільки  поділяє досконале число 10 на дві  рівні частини Пентада. - символ.природи. Інші цифри при множенні  на себе, дають  інші числа, але тільки 5 і 6 повертаються до свого  вихідного числа, в останній цифрі у добутку.

Гексада

Піфагорійці вважали, що  гексада, 6, є створення світу.Вона називалась  піфагорійцями досконалістью всіх частин, формою форм, артикуляцією Всесвіту і творцем душ. Серед ключових слів, пов'язаних з гексадою-  такі слова: "час", тому що вона вважається вимірюванням тривалості; «панацея», адже здоров'я-є  рівновагою,а гексада є рівнозначне  число; "Мир"  (3 + 2 + 1 = 6); "невтомність" тому що віна  містить елементи безсмертя.

Гептаду

Піфагорійцями називали, гептаду, 7, гідною поклоніння. Вона вважалася числом  релігій. Ключове слова до гептади-"удача", "випадок", "опіка", "рішення", «голоси», «звуки» те  що призводить речі до їх кінця.У багатьох стародавніх народів гептада є священним числом. Велика піфагорійська істина, що всі речі в природі створюються через гептадуабо 10:Число 3 (дух, розум, душа)  4 (світ)і  результатом є сума 7 або містична природа людини, яка символізована в кубі, що  має шість граней і загадкові сьому точку всередині. Шість граней є напрямки: північ, захід, південь, схід, верх, низ або землі, повітря, вогонь, вода, дух і матерія. У середині все цього  стрїть 1, що є  фігурою стоячої людини.

Огдоада

Огдоада, 8,, священне, тому що це число  першого  куба, який має вісім вершин і є парним числом, найближчим до 10 (1-2-4-8-4-2-1), вісім поділяється на дві четвірки, кожна з четвірок ділиться на двійки, і  кожна двійка  ділиться на дві одиниці, таким чином відновлюється  монада. серед ключових слів для  огдоади-"любов", "рада", "розташування", "права" та "угода".

Енеада

Эннеада, 9 була першим квадратом  непарного числа (3х3). вона була пов'язаних з помилками і недоліками, тому що їй не вистачає до  досконалої числа  10 одної одиниці.Серед її ключових слів-"океан" і "горизонт", тому що для древніх вони були  безмежні Енеада є нескінчене число, тому, що за нею немає нічого  за винятком нескінченного числа 10. Вона називається кордоном і обмеженням, тому що  збирає всі числа в собі. Вона називається сферою повітря,тому що оточує числа як повітря оточує Землю

Тетраксис – Декада

Декада, 10 ,за піфагорійцями, є найвеличніше число не тільки тому, що це тетрактис(10 точок), але також тому, що вона охоплює всі арифметичні і гармонійні пропорції. Піфагор сказав, що 10 є  природа  числа, тому, що всі народи  приходять до неї, і коли вони приходять,тоі повертаються  до  монади.Декада називалось і небо. і  миром.

Світ розвивається по законам чисел. В значках, позначаючих цифри, які ми бачимо  тисячу разів на день і навіть не задумуємость про  них ,є все знання  світу. Їх  придумали індійці. Крива лінія  символізує любов,  горизонтальна-прихильность, перехрестя їх- вибір.                                                                                                                                Одиниця стоїть нерухомо, як моноліт. Вона нічого не  відчуває,вона просто присутня.. Немає ні зігнутих , ні горизонтальних лініїй .не перехрестя. Тобто, немає ні  любові, ні прихильності, ні вибору. На рівні мінералів все несвідомо, є тут і зараз.                                                                                                                   Двійка - рівень рослин. Вигнутий стебло і горизонтальна риска  корня. Двійка прив’язана  до землі. Квітка не може рухатися. У верхній частині крива лінія. Двійка любить небо. Квітка хоче бути красивою, вона має багато кольорів .Трійка- рівень тварин. Дві вигнуті лінії вище і нижче, вона любить і небо, і землю. Трійка йде за   інстинктами. Вона  вічна рабиня  своїх почуттів. Чотири- стадія людини. Він символізує крест, перетин доріг. Перехрестя-це вибір. Якщо ми  зможемо зробити правильний вибір, перехрестя допоможе нам вийти з тваринної стадії  і перейти до наступного етапу.                                        П'ять-  стадія духа. У п'ятірки  є  верхня  горизонтальна  лінія, таким чином, вона  прив'язана до неба. Вигнута  лінія означає, що вона любить те, що  знаходитья внизу -землю . Духовні особи, зв'язаної з небом, , духовна людина любить землю.                                                                                                                                    Ось, що мав на увазі Андре Мальро в його знаменитий приказкі: " : «Третье тысячелетие будет духовным, или его не будет вовсе. Человек будет пятеркой, или его не будет вовсе.»                                                                                         

                                              Висновок      

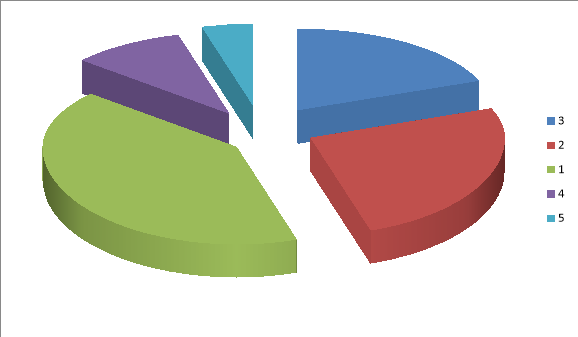
Тема «Історія виникнення чисел» актуальна в сучасному суспільстві так як на ше суспільство постійно користується числами. Світ розвивається по законам чисел. В значках, позначаючих цифри, які ми бачимо  тисячу разів на день і навіть не задумуємость про  них ,є все знання  світу.                                                                                                        Іоганн Гёте говорив: «Числа не управляют миром, но они показывают, как управляется мир».                                                                                                                                   Геометричні фигури – це конкретне втілення  чисел: число 5 зв’язується  з пентаграмою, 4 - с квадратом, 3 – з трикутником, 2 – з линиею, 1 – з  точкою.              З  геометрією було зв’язане  і  вивчення чисел. Оскільки  числа  є або раціональні, або ірраціональні, то геометрія може навести  мости між ними... Наприклад, діагональ квадрата зі стороною,що дорівнює одній  одиниці, дорівнює квадратному  кореню із 2.Термін "корінь" у фразі «квадратний корінь» має давнє походження і  має поняття взяте із  природи. Корінь рослини  прихований, але живить те, що на поверхні. Так само, приховані і корені квадратних чисел, і всі вони знаходяться в  них..Знаходження квадратних коренів було  основним заняттям стародавніх математиків. Коли квадратний корінь числа не можна  було обчислити  в цифрах ,то завжди можна було відтворивати геометрично                                                                                                                                     У стародавні часи част  обчислювали за допомогою каменців  і, звичайно, відмічали випадки, в яких можна скласти каменьці  у вигляді правильної фігури. Крім квадратних чисел були відомі трикутні  і п'ятикутні  числа                                     В ході дослідження були зробленні такі висновки:                                                                     -слово «математика»  виникло в Давній Греції приблизно в V столітті до н.е.;---лічити люди навчилися з незапам’ятних часів;                                                             -необхідність позначення чисел привела до утворення спеціальних знаків –цифр;                                                                                                                                                -існують різні теорії виникнення чисел;                                                                      -геометричні фігури –конкретне втілення чисел;                                                                     .  Якщо по аналогії з буквенним Алфавітом вести поняття»Цифровий Алфавіт»,то його базову основу складуть десять ісходних знаков-символів:1,2,3,4,5,6.7,8,9.Їх можна назвати»простими» цифровими зображенями чисел.Цифровий символ «0»використовується в системі письма  для відображення відсутності числа.Для позначення всіх останніх чисел,більших від числа 9,необхідно використовувати  об’єднання вихідних символів,які по відношеню до «простих» зображень чисел,є «составними».Я провела дослідження:учням нашої школи,учителям і знайомим я звернулась з питанням:»Чи знаєте ви історію виникнення чисел?»                                                                               «Чи існує зв'язок між числами і геометрією?»                                                                                            На перше питання:                                                                                                                                                  1) 40%відповіли,що знайомі з невеликою кількістю фактів із історії виникнення чисел;                                                                                                                                                2) 25% відповіли,що знайомі з достатньою кількістю фактів із історії виникнення чисел;                                                                                                                                                                    3) 20%-знають тільки два або три факти із історії виникнення чисел;                                                4) 10%знайоми з одним історичним фактом;                                                                                                                  5) 5%-не знають не одного історичного факту;                                                                                                          На друге більшість опитуванних відповіли,що з такими фактами незнайомі.                                                 Отже матеріали дослідження можна рекомендувати до використання на уроках математики ,для  додаткових занять з математики,для пізнавального читання.

                                      Література

1. Я.Познаю світ. Дитяча енциклопедія: Математика/ Я 11Авт.-сост. О.П. Савін та інших.: - М.: ТОВ "Видавництво АСТ", 2001.

2.Г.И.Гейзер. Історія математики школі. Посібник для вчителів. – М.: Просвітництво, 1981.

3.Г.Н.Берман Кількість і наука про неї.Общедоступние нариси. Москва:Гос. виданнятехнико – технічної літератури 1984.

4. І.Депман. Світ чисел. Розповіді про математиці. Ленінград "Дитяча література" 1988.

5.Я.И. Перельман. Жива математика. Математичні розповіді та головоломки. М: Тріада – літера 1994.

6.И.Я.Депман.Н.Я.Виленкин. За сторінками підручника математики. Посібник учнів 5-6 класів.Издательство"Просвещение" 1989.

7.Е.Карпеченко Таємниці чисел .Математика />Прил. До газеті "Перше вересня" №13 2007.

8.А.Н.Крилов.Числа й відчуття міри. Математика/Прил. До газеті "Першесентября"№7 1994

9. Internet ресурси