Творча робота вчителя як засіб розвитку мотивації уміння молодших школярів на уроках математики

Творча робота вчителя як засіб розвитку мотивації уміння молодших школярів на уроках математики
 

Шановні доброчинці! Я вважаю, що  успіх будь-якої діяльності залежить не лише від здібностей і знань, а й від мотивації, тобто від прагнень самостверджуватися, досягати високих результатів. Адже чим вищий рівень мотивації, чим більше чинників спонукають дитину до діяльності, тим більших результатів вона може досягти.

Кожен учитель хоче, щоб його учні добре навчалися, з інтересом і бажанням ходили до школи. У цьому зацікавлені і батьки учнів.

Перед школою стоїть завдання - розвинути в дитини позитивну мотивацію до навчальної діяльності.

Адже для того, аби учень по-справжньому включився в роботу, потрібно, щоб завдання, які ставляться перед ним під час навчальної діяльності, були не тільки зрозумілі, а й прийняті школярем, тобто були для нього значущі.

Відомо, що розвиток мотивів навчання відбува­ється: через засвоєння учнями суспільного змісту навчання, або через саму навчальну діяльність школяра, що має чимось його зацікавити.

На мою думку, головне завдання вчителя полягає в тому, щоб, з одного боку, донести до свідомості дитини ті моти­ви, що суспільно незначущі, але мають досить висо­кий рівень дієвості. Прикладом може бути бажання одержувати гарні оцінки. Учневі необхідно допомог­ти усвідомити об'єктивний зв'язок оцінки з рівнем знань та вмінь. І в такий спосіб поступово підійти до мотивації, пов'язані з бажанням мати високий рі­вень знань і умінь. Це, у свою чергу, має усвідомлю­ватися дітьми як необхідна умова їхньої успішної, корисної суспільству діяльності. З іншого боку, необхідно підвищити дієвість мотивів, що усвідомлю­ються як важливі, але реально на їхню поведінку не впливають.

Хочу навести приклади творчих завдань, які потрібно застосовувати на ступені формування вмінь і нави­чок розв'язувати прості текстові задачі на додавання і віднімання.

1. У саду росло 9 вишень, а яблунь — на 3 менше. Скільки яблунь росло в саду?

— Поясніть, чому задача розв'язується так: від числа 9 відняти 3. Буде 6.

— Якщо в саду росло 9 вишень, а яблунь — на З менше, то яблунь росло стільки, скільки вишень, але без трьох. Треба від числа 9 відняти 3, буде 6.

2. Петрусь намалював 5 ялинок, а беріз — на дві менше. Скільки беріз намалював Петрусь?

— Якою дією треба розв'язати задачу? Поясніть.

— Задачу треба розв'язати дією віднімання. Якщо Петрусь намалював 9 ялинок, а беріз — на дві мен­ше, то беріз він намалював стільки, скільки ялинок, але без двох. Треба від числа 5 відняти 2, буде 3.

3. За день у магазині продали 6 телевізорів, а радіоприймачів — на 4 менше. Скільки радіоприймачів продав магазин за день ?

— Який із прикладів є розв'язком задачі: 6 + 4 чи 6-4? Поясніть.

— Приклад 6 - 4 є розв'язком задачі. Якщо за день у магазині продали 6 телевізорів, а радіоприй­мачів — на 4 менше, то радіоприймачів продали стільки, скільки телевізорів, але без чотирьох.

4. Задача 1. У Петруся було 6 білих голубів, а сірих — на 3 менше.

 Скільки сірих голубів було у Петруся?

Задача 2. У букеті було 6 білих троянд, а черво­них — на 3 більше.

Скільки червоних троянд було в букеті?

— Що спільного в цих задачах?

— У цих задачах спільними є числа.

— Чим відрізняються ці задачі?

— У першій задачі говориться про голубів, у дру­гій — про троянди.

В першій задачі: сірих голубів — на 3 менше, в другій — червоних троянд на 3 більше.

— Прочитайте розв'язання першої задачі.

— Від числа 6 відняти 3. Буде 3.

— Прочитайте розв'язання другої задачі.

— До числа 6 додати 3. Буде 9.

— Що спільного в розв'язанні цих задач?

— У розв'язанні цих задач однакові числа.

— Чим відрізняються розв'язання цих задач?

— Задачі розв'язуються різними діями. Перша за­дача розв'язується дією віднімання, а друга — дією додавання. В задачах — різні результати і відповіді.

Як видно із розглянутих прикладів, уроки матема­тики дають великі можливості для органічного поєднання роботи над питаннями культури мовлен­ня з вивченням початкового курсу математики, що відображає педагогічні погляди В.Сухомлинського і його концепцію навчальної діяльності, згідно з якою мовленнєва культура є обов'язковою складовою розвитку учнів.

Поступово завдання ускладнюються. Під керів­ництвом учителя школярі порівнюють задачі, аналі­зують їх, що дає змогу продовжити цю роботу над складними задачами. Наприклад.

Задача. Дівчатка зібрали 18 кг лікарських рос­лин, а хлопчики — у 6 разів менше. Скільки кілограмів лікарських рослин зібрали діти?

Дівчатка — 18 кг                                            2) +

1):                                                      ?

Хлопчики — ?, у 6 разів менше

Аналізуємо задачу, пояснюючи добір дій, став­лячи знак дії біля знаків питання. Діти складають короткий запис задачі колективно. Учень працює біля дошки.

Зразок міркування.

Головне запитання задачі — Скільки кілограмів лікарських рослин зібрали іти? Це буде остання (друга) дія задачі. Знаходимо суму тому, що зібрані рослини об'єднались — це буде дія додавання, став­лю знак плюс.

Спочатку знайду, скільки кілограмів лікарських рослин зібрали хлопчики. Виконуватиму дію ділення тому, що вони зібрали у 6 разів менше. Це буде пер­ша дія. Ставлю знак ділення.

Перед самостійним розв'язуванням задачі, ставлю дітям запитання: "Хто може сам розв'язати задачу?". Діти піднімають руки і починають працювати. Хто не може сам упоратися, піл юдить до вчителя. Ми усно розв'язуємо задачу без обчислення дій. Потім діти сідають на місце і вже впевнено виконують за­дачу самостійно.

Короткий запис задачі, поєднаний з її аналізом, дає змогу учневі наочно і бачити взаємозв'язок слів чисел і дій, допоможе скласти план виконання і пояснення до кожної дії задачі, знайти правильний хід розв'язку.

Особливу увагу у роботі з учнями приділяю  розв'язуванню системи завдань з логічним навантаженням. Найбільшу творчу активність у них і викликають завдання, що сприяють формуванню уміння аналізували, порівнювати, класифікувати математичні об'єкти.

У підготовчих вправах переважно застосовується порівняння. Це завдання виду: вилучити або назвати зайвий предмет, намалювати фігуру такого ж кольору (форми, розміру), дати назву групі предметів, порівняти схожі малюнки і знайти відмінності тощо.

Перші вправи на проведеним класифікації виконуються за однією ознакою, відбувається розбиття на дві групи (такі й не такі).

1. Назвіть номери фігур, що: а) є чотирикутниками; б) не є чотирикутниками; в) є трикутниками; г) не є многокутниками; д) не є прямокутниками.

 

 

 

 

 

 

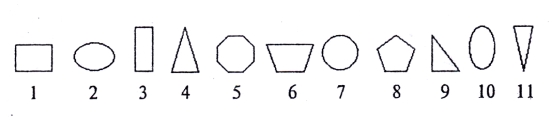
2. Розбийте числа на групи: у першу запишіть числа менші, ніж 8, а в другу — більші, ніж 8: 1, 2, З, 6, 7, 9, 10.

3. Розв'яжіть спочатку приклади зі зменшуваним 17, а потім решту:

18-17  17-9  17+0

17 + 1  9 + 8  17-8

4. Випишіть приклади з відповіддю 12 і 6:

5+6  6+5  13 – 6  6+6

7 + 7  13-1  9+3  14-8

5. Розбийте приклади на групи. В першу запишіть приклади, відповіддю яких будуть одноцифрові числа, в другу — приклади, відповіддю яких будуть двоцифрові числа:

37 – 7  15-6  59-10  48+1

37 – 30 100-1  59-50  27+30

Завдання, в яких потрібно виділити об'єкти за певною основою, а потім вказати основу для групи об'єктів, що залишились.

1. Випишіть числа, в яких десятків менше, ніж 3. Випишіть числа, в яких десятків більше, ніж 3:

46, 21, 34, 67, 55, 17, 38, 13, 84, 71, 30.

(Для групи чисел, що залишились, учні повинні визначити спільну основу).

2. Випишіть всі числа, записані двома різними цифрами:

22, 56, 80, 66, 74, 47, 88, 31, 94, 44.

(Для чисел, що залишились, назвати спільну ознаку, основу класифікації).

Завдання на визначення основи для виконання класифікації об'єктів.

1. Розбийте числа на групи, щоб у кожній були схожі між собою числа:

38, 62, 84, 30, 61, 89, 32, 68.

І — числа, що мають 3 десятки (38, 30, 32); II — числа, що мають 6 десятків (62, 64, 68); III — числа, що мають 8 десятків (84, 89).

2. Розв'яжіть приклади і розподіліть їх на групи: 3+2, 4+5, 4+1, 6-3, 9-2, 10-1, 6+4, 6+1, 3+4.

(В основу розподілу можна покласти арифметичну дію або відповідь).

3. Розкладіть іменовані числа на групи: 30 м, 8 кг, 17 л, 1 год, 100 кг, 94 дм, 40 хв, 63 см, 10 хв, 55 м, 22 л, 24 год.

Завдання на визначення основи, за якою виконана класифікація.

1. Чим схожі собою приклади у кожному рядку:

11 + 5  11+  12+4

10-8  12-1  9-5

(В основу класифікації взято арифметичну дію).

2. За якою ознакою записано стовпчики при­кладів:

27 + 5 79 +20 44 + 2

39 + 6 59 +30 34 + 5

29 + 3 35 +40 32 + 6

(В основу класифікації взято обчислювальний прийом).

Для ознайомлення зі спрощеними прийомами запам'ятовування і відтворення вивченого використовую прийоми "Школи ейдетики". Так, за допомогою малюнків і казкового сюжету ми вивчили табличку множення, вміємо вчити напам'ять віршовані і прозові тексти за допомогою піктограм ("малюнкового" письма), ознайомилися і використовуємо прийоми ейдетики для вивчення іноземної мови.

Велике поле для творчої діяльності надають нам інтерактивні методи навчання.

Серед інтерактивних методів навчання я віддаю   перевагу "криголамам", побудові асоціативного куща, читанню із зупинками, модельному уроку, грі "Та-ні".

Зупинимося  на методі, який має назву "побудова асоціативного куща". логічного дерева, гірлянди асоціацій. Фактично вчитель визначає тему одним словом, а учні згадують все, що виникає у пам'яті стосовно цього словаї

Наприклад у 1-му класі під час вивчення теми "Нумерація в межах 10" виникає проблема активізації класу щоразу, коли вводиться нове число. До вашої уваги фрагмент активізації класу на уроці "Число і цифра 7".

Вчитель. Усі ми використовували слово сім. Згадайте, де воно вам зустрічалося?

Учень 1. У казці "Вовк і семеро козенят".

Вчитель. Так, правильно. А ще коли?

Учень 2.  Сім кольорів веселки.

Учень 3.  Білосніжка і семеро гномів.

Учень 4.  Сім нот: до, ре, мі, фа, соль, ля, сі.

Учень 5.   Сім'я.

      Учень 6.  У прислів’ях: Семеро одного не чекають. Сім разів відміряй - один раз відріж.

Учень 7.  Сім чудес світу.

Учень 8.  Мені сім років.

Учень 9.   Я живу на сьомому поверсі.

 

Вчитель. Так, зі словом сім ви знайомі вже давно, а в математиці для його позначення існує число і цифра 7.

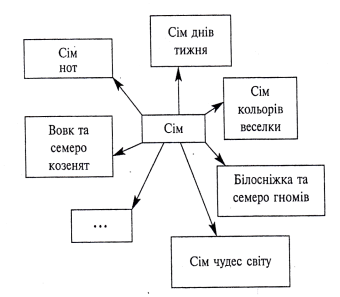Оскільки йдеться це про урок у 1 класі, я використовую підготовлені ілюстрації або малюнки ( веселка, календар, ноти, фрагменти казок тощо). Для того, щоб діти звикали до схематичної побудови асоціативного куща, за допомогою магнітів або скотча закріплюю на дошці підготовлене унаочнення (відповіді дітей легко спрогнозувати) у формі куща, як показано на малюнку. Отже, на дошці перед очима дітей виникає (за їхніми відповідями) цікавий "кущ", на "гілках" якого знаходяться відомі ілюстрації.

 

 

 

 

 

 

 

 

 

 

 

 

• А як на вашу думку отримується число сім? Якщо ми уважно розглянемо ілюстрацію казки «Вовк та семеро козенят», то побачимо, що сьоме козеня прибігло до перших шести. Отже, якщо до шести додати один, отримаємо нове число 7.

 

Шановні колеги, тож пам’ятаємо:
 

Ми той місточок-кладочка,

Що в’яже все у в’язочку -

Минуле із теперішнім,

Сьогодні з майбуттям.

Для красоти життя

І радості буття.