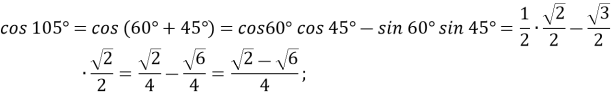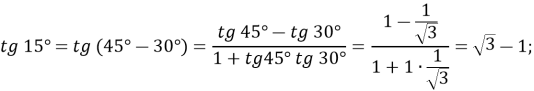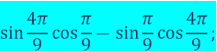МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ДНІПРОВСЬКИЙ ТРАНСПОРТНО-ЕКОНОМІЧНИЙ ФАХОВИЙ КОЛЕДЖ

ЦК математики та ПНП

ЗАТВЕРДЖУЮ

Заступник  директора з навч. роботи

___________Надія УЛАСЕВИЧ

«___»_____________2021р

«Українська мова та математика. Говори правильно»

Методична розробка

навчального заняття з математики

«Перетворення сум тригонометричних функцій»

(до Дня української мови та писемності)

Розроблена

Викладачем вищої категорії

Арнаут Катерина.

Розглянуто і ухвалено

ЦК математики та ПНП

Протокол №__ від ___________р.

голова комісії  Ольга КАБАНЕЦЬ

2021

Зміст

Вступ

І. Оргмомент.

ІІ. Українська мова та математика .

До дня української мови та писемності.

ІІІ. Актуалізація опорних знань.

ІV. Мотивація навчальної діяльності.

V. Пояснення нового матеріалу .

VІ. Закріплення нових знань і вмінь учнів

VIІ. Підсумок заняття

VIІІ. Домашнє завдання.

ВИСНОВКИ

ІНФОРМАЦІЙНІ ДЖЕРЕЛА

ДОДАТОК 1

ДОДАТОК 2

ДОДАТОК 3

ДОДАТОК 4

Вступ

Тригонометрія – є однією з найважливіших складових елементарної математики. Мета даної навчально-методичної розробки – допомогти студентам опанувати основні способи перетворення суми та різниці тригонометричних функцій в добуток.

Актуальність теми полягає в тому, що підготовка висококваліфікованих фахівців технічних спеціальностей вимагає від педагогічної науки перегляду і дослідження проблеми викладання предмету «Математика». Така необхідність пов’язана з соціально-економічними змінами у суспільстві, з підвищенням вимог до спеціалістів, до їх активності та відповідальності у відношенні до професійного та особистісного розвитку.

Формування компетентностей:

• Предметна компетентність: формувати вміння застосовувати формули перетворення суми та різниці тригонометричних функцій до перетворення тригонометричних виразів
• Ключові компетентності:
• спілкування державною мовою – ставити запитання і розпізнавати проблему; міркувати, робити висновки на основі інформації, грамотно висловлюватися рідною мовою, доречно та коректно вживати в мовленні математичну термінологію;
• уміння вчитися впродовж життя – організовувати та планувати свою навчальну діяльність., моделювати власну освітню траєкторію;
• інформаційно-цифрова – діяти за алгоритмом та складати алгоритм;
• соціальна та громадянська компетентність – співпрацювати в команді, виділяти і виконувати власну роль у командній роботі, висловлювати власну думку, слухати та чути інших.

Тема: Українська мова та математика. Говори правильно.

Формули перетворення суми та різниці тригонометричних функцій у добуток

Мета: вивчити формули перетворення суми та різниці тригонометричних функцій у добуток; формувати вміння застосовувати їх до перетворення тригонометричних виразів; розвивати логічне мислення учнів, їх пізнавальну активність, ініціативу, культуру математичного мовлення; виховувати наполегливість, старанність, толерантність, комунікабельність.

Хід заняття

І. Оргмомент.

Перевірка готовності учнів до уроку. налаштування на роботу.

ІІ. Українська мова та математика .

До дня української мови та писемності.

Українська мова- це не лише мова художніх творів. Сучасна українська мова обслуговує усі сфери діяльності людства. Має офіційну, технічну, спортивну термінологію тощо. Наше завдання не калькувати з російської мови, а знати питому україністку термінологію.

Демонструється відео «Натуральні числа та українська мова »

(ДОДАТОК 1)

Точаться дискусії, чи є в українській мові слово точка? Розділовий знак чи цятка – це дійсно крапка. Але! Геометричний об’єкт – це точка. Точка перетину, точка відліку, матеріальна точка.

І запам’ятайте! Числа українською додатні, а не позитивні, хоча так хочеться, щоб вони були милими та привітними.

Якщо ж ви обмежуєте рух тіла, іншим тілом, то ви встановлюєте в’язь, а не зв’язки між цими тілами.

Тож знайдіть точку опори і переверніть цей світ!

Демонструється відео «Основні терміни українською. Говори правильно »

(ДОДАТОК 2)

Студентам пропонується пройти вікторину, що проводиться на офіційній сторінці інстаграм коледжу @dacte_ua

(ДОДАТОК 3)

ІІІ. Актуалізація опорних знань.

Інтерактивна вправа « Установити відповідність».

(Завдання студенти бачать на екрані, викладачем надається доступ студентам до функції малювання на екрані, за допомогою цієї функції студенти з’єднують відповідні назви та формули)

1. Спростити вирази:

1.  
2. 
3. 
4. ;
5. 
6. 

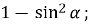
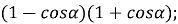
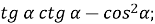
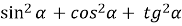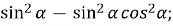
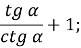
Розв’язання:

1. ;
2. ;
3. 
4. 
5. ;
6. 

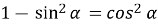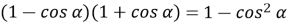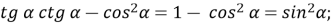
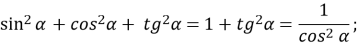
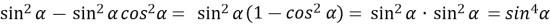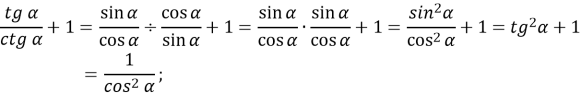
ІV. Мотивація навчальної діяльності.

На попередніх заняттях ми виконували тотожні перетворення тригонометричних функцій одного й того самого аргументу, на цьому занятті ми доведемо тригонометричні тотожності додавання для двох різних кутів.

V. Пояснення нового матеріалу .

Викладач наводить доведення формули

(показ презентації )

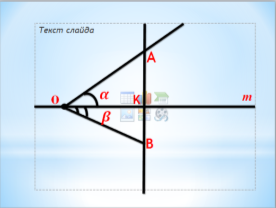
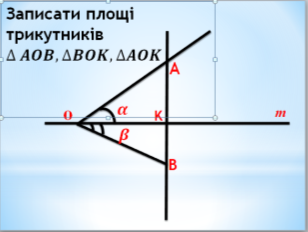
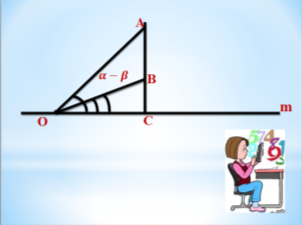
Візьмемо довільну пряму m і точку О на ній. Відкладемо два різні гострі кути в в різні півплощини, так що . З точки К  проводимо перпендикуляр до перетину зі сторонами кутів у точках А і В відповідно. Дістанемо .

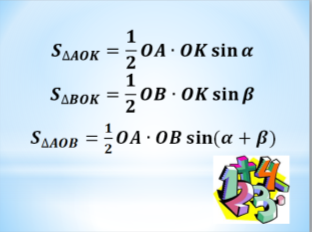
Аналогічно доводитимемо .

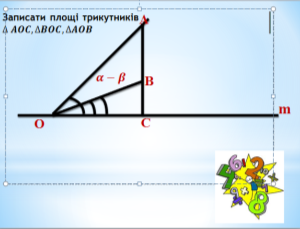
Візьмемо довільну пряму m і точку О на ній. Відкладемо два різні гострі кути в одну півплощину, так що . Із будь-якої точки С , (C), проводимо перпендикуляр до перетину зі сторонами кутів У точках А і В відповідно. Дістанемо:

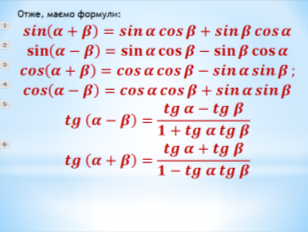
VІ. Закріплення нових знань і вмінь учнів

Розв’язування вправ усно.

(Завдання екрані, викладач поступово записує розв’язок, студенти коментують ). Завдання до всієї групи.

1. Закінчіть обчислення:

Розв’язання:

Розв’язування вправ письмово.

(Завдання екрані, викладач поступово записує розв’язок, студентам по черзі надається доступ до режиму малювання). Завдання до всієї групи.

2. Знайти значення виразу:

Розв’язання:

1. 
2. ;
3. 
4. ;
5. 

3. Обчислити

1. обчислити ;
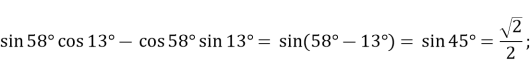
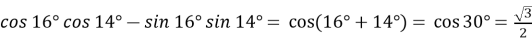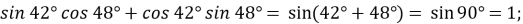
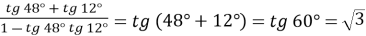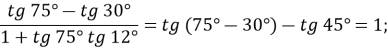
2.  обчислити ;

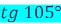Розв’язання:

№1

№2

4. Знайдіть значення виразу:

Розв’язання

1. 
2. 
3. 
4. 
5. ;
6. 

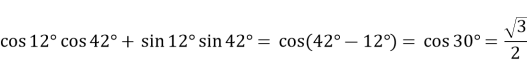
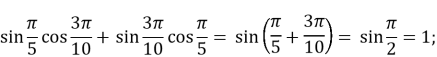
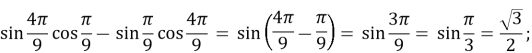
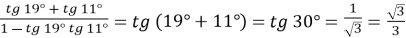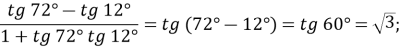
VIІ. Підсумок заняття

Вправа «Мікрофон»:

• Ми повторювали…
• Доводили…
• Вчилися…
• Застосовували…
• Удосконалювали
• Чому дорівнює
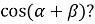
• Чому дорівнює
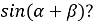
• Чому дорівнює
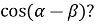
• Чому дорівнює
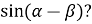
• Чому дорівнює

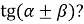
Аргументовне оцінювання знань студентів викладачем

VIІІ. Домашнє завдання.

1. Спростити вирази:

2. (Високий рівень)

Довести формули для

ВИСНОВКИ

Тригонометричні перетворення одна з найскладніших тем у курсі математики. Тригонометричні функції застосовують при вирішенні завдань по планіметрії, стереометрії, астрономії, фізики і в інших областях.

На сьогоднішньому занятті Ви зуміли як застосувати свої знання на практиці, обмінялися знаннями, оцінили свою діяльність на занятті та отримали можливість замислитись над підвищенням якості  роботи, оцінивши свій рейтинг.

Не менш важливим аспектом, який ми з’ясували на занятті – коректність та правильність вживання математичних термінів, правил, означень державною мовою.

ІНФОРМАЦІЙНІ ДЖЕРЕЛА

1. Математика 10 клас А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський, М. С. Якір 2018. Алгебра і початки аналізу та геометрія.
2. Математика 10 клас О.С. Істер 2018. Алгебра і початки аналізу та геометрія.
3. Математика 10 клас Г. П. Бевз, В. Г. Бевз 2011. Рівень стандарту.
4. Капіносов А., Білоусова Г., Гап'юк Г., О.Чиж  Посібник для підготовки до ЗНО  2014 з математики.
5. Мірошин В. Відбір коренів у тригонометричних рівняннях // Математика. Додаток до газети  «Перше вересня».– 2006.– № 17.
6. Смоляков А.Н., Севрюков П.Ф. Прийоми рішення тригонометричних рівнянь // Математика в школі. – 2004. – № 1.
7. Шабашова О.В. Прийоми відбору коренів у тригонометричних рівняннях // Математика в школі. – 2004.– № 1.
8. Шкіль М. І., Слєпкань З. І., Дубинчук О. С  Алгебра і початки аналізу // Підруч. для 10 кл. загальноосвіт. навч. закладів.–К.: Зодіак – ЕКО. –2002.

ДОДАТОК 1

ДОДАТОК 2

ДОДАТОК 3

ДОДАТОК 4

Теоретичні відомості за програмою з тригонометрії

Основні означення

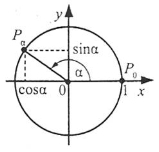Синусом числа α називається ордината точки Р_α, утвореної пово­ротом точки Р_α (1; 0) навколо початку координат на кут в α раді­ан (позначається sin α).

Синус визначений для будь-якого числа α.

Значення синуса змінюється від  (-1) до 1, тобто

Косинусом числа α називається абсциса точки Р_α, утвореної по­воротом точки Р_α (1; 0) навколо початку координат на кут в α радіан (позначається cos α)

    Косинус визначений для будь-якого числа α. Значення косинуса змінюється від  (-1) до 1, тобто   .

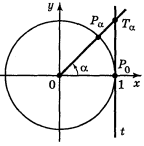Тангенсом числа α називається відношення синуса числа α до його косинуса:        .

Тангенс визначений для всіх а, крім тих значень, для яких cos α = 0, тобто, α = + πn, n Ζ.

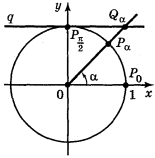Котангенсом числа α називається від­ношення косинуса числа α до його синуса:   .

Котангенс визначений для всіх α, крім таких значень, для яких sin α 0, тобто, a = π n, n Ζ.

Знаки тригонометричних функцій.

Таблиця значень тригонометричних функцій деяких кутів

Співвідношення між тригонометричними функціями

одного і того ж аргументу

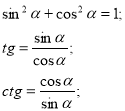
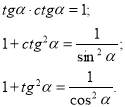
Формули зведення

Формули додавання

;                                   ;

;                          ;

                          ;

;                          

Формули подвійного аргументу

;

Формули половинного аргументу

;

;

;

;

;;

;

Формули перетворення суми і різниці тригонометричних функцій

у добуток

;

;

;

;

;

;

;

Формули перетворення добутку функцій

;

Формули пониженого степеня

Графік функції

Крива, яка є графіком функції у = sin x, називається синусої­дою.

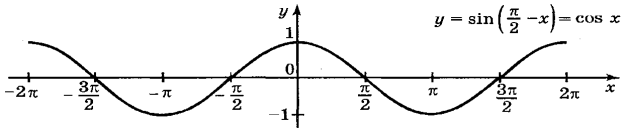
Графік функції

Крива, яка є графіком функції у = cos x, називається косинусої­дою.

Графік функції

Графік функції у = tg x називається тангенсоїдою.

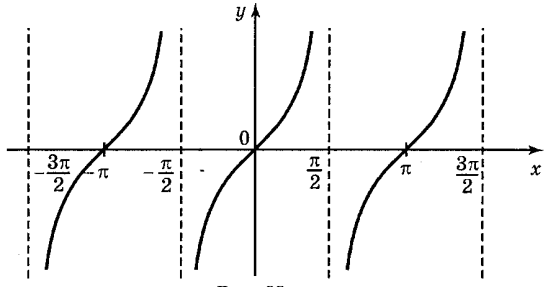
Графік функції

Графік функції у = tg x називається котангенсоїдою.

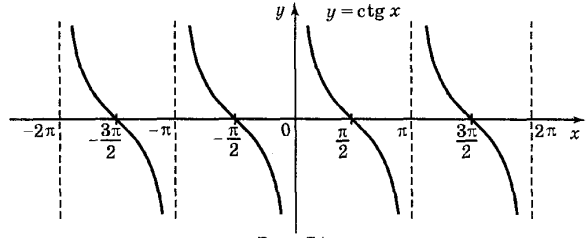
Властивості тригонометричних функцій