Стебненська ЗОШ І-ІІІ ст.

Звенигородської райради

 Черкаської області

Вчитель математики

 Лисогор Таміла Веніамінівна

 

Захист навчального проекту

Теорема Піфагора на службі у людини 

План навчального проекту

Опис проекту
Назва проекту:		Теорема Піфагора на службі у людини
Основні питання:
	Ключове питання:	Чи варто вчити теорему Піфагора ?
	Тематичні питання:	Піфагор – легенда і джерело дискусій? Які методи доведення теореми існують? Як допомагає теорема Піфагора при розв’язуванні задач?
	Змістові питання:	Хто такий Піфагор? Де жив і працював Піфагор? Як формулюється теорема Піфагора?
Стислий опис:
В процесі роботи над проектом восьмикласники поглиблюють свої знання з історії математики, програмового матеріалу з геометрії; відшукують цікаві задачі, вчаться застосовувати теорему Піфагора при розв’язуванні задач. Школярі набувають навиків самостійної роботи з додатковою літературою, закріплюють уміння працювати на комп’ютері. Учні створять публікацію, презентацію з конкретного питання, оцінять результати своїх досліджень. Діти набувають навиків організації колективної та групової роботи.

Навчальні предмети, з якими пов'язаний проект: історія, географія, українська література, мистецтво

Державні освітні стандарти та навчальні програми:

Основною метою освітньої галузі є:

- опанування учнями системи математичних знань, навичок і умінь, необхідних у повсякденному житті та майбутній трудовій діяльності, достатніх для успішного оволодіння іншими освітніми галузями знань і забезпечення неперервної освіти;

- формування в учнів наукового світогляду, уявлень про ідеї і методи математики, її роль у пізнанні дійсності;

- інтелектуальний розвиток учнів (логічного мислення і просторової уяви, алгоритмічної, інформаційної та графічної культури, пам'яті, уваги, інтуїції);

- економічне, екологічне, естетичне, громадянське виховання, формування позитивних рис особистості.

Зміст освітньої галузі формується за принципом наступності між початковою, основною і старшою школою, враховуючи математичну підготовку учнів початкової школи за змістовими лініями освітньої галузі "Математика".

         Мета проекту:

 - виховання в учнів інтересу до вивчення математики;

 - ознайомлення восьмикласників з життєвим шляхом давньогрецького вченого Піфагора Самоського, історєю та способами доведення теореми Піфагора;

 - вироблення у школярів практичних навиків у використанні теореми Піфагора;

 - формування у дітей умінь працювати з додатковою літературою.

Очікувані результати:

Після виконання проекту учні

 глибоко засвоять теорему Піфагора;

 ознайомляться з життям і діяльністю Піфагора Самоського;

 зацікавляться історією математики;

 вдосконалять навики роботи на комп’ютері;

 навчаться працювати з різними джерелами інформації.

 

Приблизний час, необхідний для реалізації навчального проекту:
Від 4 до 8 тижнів
Вхідні знання та навички:
Учні мають уявлення про прямокутний трикутник, знають означення косинуса гострого кута прямокутного трикутника. Вони вміють користуватися комп’ютером.
Диференціація навчання:
Обдаровані учні:	Задачі підвищеної складності, олімпіадного характеру
Оцінювання знань та вмінь учнів:		оцінювання знань учнів відбувається вчителем через опитування, тести, контрольні роботи, учнівські роботи
Ключові слова:		Прямокутний трикутник, гіпотенуза, катет, теорема, доведення

 

Обладнання: комп'ютерна презентація Microsoft PowerPoint, картки із завданнями.

     Тип уроку: урок – захист проекту.

Найкращий з усіх скарбів – знання.

 Його не можна ні вкрасти, ні загубити, ні знищити.

                                                                            Г. Сковорода

український просвітитель-гуманіст, філософ, поет, педагог.

ХІД УРОКУ

1. Організаційний момент.
2. Актуалізація опорних знань.

 Я пропоную вам  опрацювати кросворд. Знайти ключове слово

( робота в групах)

 

 

 

Кросворд

1. Відрізок, що лежить на прямій, перпендикулярній до заданої прямої і з кінцями в заданій точці, і точки, що лежить на заданій прямій.
2. Сторона прямокутного трикутника, яка лежить навпроти прямого кута
3. Множина точок на площині, яка обмежена скінченим числом ліній.
4. Відрізок, який з'єднує вершину трикутника з серединою протилежної сторони
5. Одиниця вимірювання плоского кута
6. Відрізок, проведений з вершини трикутника до прямої, яка містить сторону протилежну вершині та перпендикулярний до неї.
7. Відрізок, що сполучає кінець перпендикуляра і похилої 

 

 

 

 

п

е

р

п

е

н

д

и

к

у

л

я

р

г

і

п

о

т

е

н

у

з

а

ф

і

г

у

р

а

м

е

д

і

а

н

а

г

р

а

д

у

с

в

и

с

о

т

а

п

р

о

е

к

ц

і

я

     

580 до н. е. — 497 до н. е., давньогрецький філософ

 Мотивація навчальної діяльності учнів.

     Учитель. Відомо, що в давнину люди спостерігали за світилами і вели календар; розраховували строки посіву, час розливу рік; орієнтувалися по зірках, прокладаючи маршрути морем і сушею.

     Усе це призвело до використання геометричних задач на практиці.   

Захист проекту

 Сьогодні на уроці ми почуємо захист проекту. Тема нашого проекту „ Теорема Піфагора  на службі у людини”. Учні  класу об’єдналися у 3 групи, кожна з яких зайнялася дослідженням свого питання:

 історики – „Піфагор – легенда і джерело дискусій” ( Хто такий Піфагор?

Де жив і працював Піфагор?);

теоретики – „Різні способи доведення теореми Піфагора” (Як формулюється теорема Піфагора? Які методи доведення теореми існують?);

 практики – „Застосування теореми Піфагора до розв’язання задач” (Як допомагає теорема Піфагора при розв’язуванні задач?).

 Вчитель. В оцій ось скринці – священна таємниця древніх. Їхні жреці як божественне одкровення сприймали математичні істини, пильнували й використовували. Так минали століття.

Історики (Усний журнал)

УЧЕНЬ. Клубочиться дим над жертовником дельфійського оракула і в глухому шумі прибою чується уривчасте бурмотіння піфії. Її судорожні зітхання й незбагненні слова оракул тлумачив у коротких реченнях:

• Море … подорож…Ти, жінко, народиш сина…

Славний син… для всіх віків і народів…

• Боги чекають ім’я …
• Хай буде Піфагором… пророчений піфією

(Олесь Бердник «Покривало Ізіди» (під муз. супровід)

Учень. Вважають, що Піфагор, народившись на острові Самос в Егейському морі, за науками помандрував до Єгипту, як полонений потрапив у Вавилон, а далі опинився в Індії. Саме він розкрив секрети брамінів Греції та й усьому світові. Дійшли вони і до Київської Русі.

Учень. Перед тим, як закласти нові підвалини, ще раз переміряли розташування церкви, щоб вона стояла в точній відповідності до сторін світу. Використовувався для цього шнур з трьома вузлами, які розташовані між собою на віддалі, що вимірюється відповідно числами 3,4 і 5 однакових проміжків. Із шнура творився трикутник…

( Павло  Загребельний, «Диво»)

Вчитель.  Заглянемо ж тепер до скриньки. Ось , вона загадка, освячена віками… Звичайнісінька мотузка з вузлами – предтеча найславетнішої теореми, заслужено названої Піфагоровою.

До речі. Єгипетський трикутник – єдиний прямокутний трикутник, у якого сторони рівні трьом послідовним цілим числам 3,4,5 для якого 5²=3²+4²

Повідомлення учня  (історична довідка)

1.Відкриття теореми Піфагора оточено ореолом красивих легенд.

 Переказують, що на честь такого відкриття Піфагор приніс  гекатомбу – жертву із ста биків. А втім, якщо вчений справді був у Вавілонії, він міг довідатися про те, що шумеро-вавілонські математики знали і використовували під час розв’язування задач теорему, названу пізніше його ім’ям, за багато років до народження Піфагора.

2.Теорема Піфагора має народні назви. 

 У Франції і деяких областях Німеччини в середні віки її називали „ослиним мостом”, тому що доведення теореми було величезною перешкодою, так званим мостом, перейти який могли тільки розумні учні.

 У математиків арабського Сходу ця теорема одержала назву „теореми нареченої”. Справа в тому, що в деяких списках „Начал” Евкліда ця теорема називалася „теоремою німфи” за подібність креслення з метеликом, що грецькою звався німфою. Але цим словом греки називали деяких богинь, а також наречених. При перекладі арабський перекладач, не звернувши уваги на креслення, переклав слово „німфа” як „наречена”, а не „метелик”.

 А відома всім школярам назва „Піфагорові штани” виникла через схожість креслення до Евклідового доведення теореми зі штанами.

 

 

 

 

 

 Теоретики – „Різні способи доведення теореми Піфагора” (Як формулюється теорема Піфагора? Які методи доведення теореми існують?);

 

Учень.

Класичне формування теореми Піфагора: якщо сторони прямокутного трикутника є сторонами квадратів, то площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів, побудованих на катетах.

 Теорема Піфагора чудова тим, що вона зовсім не очевидна. Із простого споглядання прямокутного трикутника не зробиш висновок, що між його сторонами є таке просте співвідношення: с² = а² + в²

В ході опрацювання літератури ми склали діаграму: яка показує, що можна використати для доведення теореми Піфагора:

 1) Основні тригонометричні  тотожності;

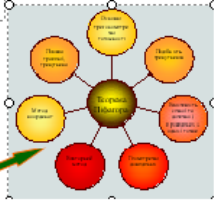 2) Площа трапеції, трикутника, квадрата;

 3) Метод координат;

 4) Векторний метод;

 5) Геометричні доведення;

 6) Подібність трикутників;

 7) Властивість січної та дотичної, проведених з однієї точки;

            8) арифметичний спосіб

Приклади доведення теореми.(презентація) Подорож до музею (відео)

 

Практики – „Застосування теореми Піфагора до розв’язання задач” (Як допомагає теорема Піфагора при розв’язуванні задач?). (презентація)

Слова учителя :

Застосування математики до рішення завдань з будь-якої іншої області включає наступні три етапи:

 

1) переклад запропонованого завдання мовою відповідної для її вирішення математичної теорії (побудова математичної моделі завдання);

 

2) рішення задачі у рамках математичної теорії, мовою якої вона перекладена (рішення задачі усередині моделі);

 

3) зворотний переклад результату рішення на мову, на якій було сформульовано початкове завдання (інтерпретація отриманого рішення).

 

 

Історичні задачі. Усне розв'язування історичних  задач (з  наступним коментуванням) Калейдоскоп задач

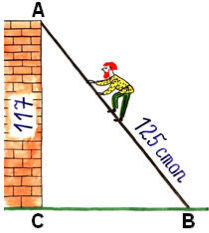
     Задача 1. Завдання з підручника "Арифметики" Леонтія Магницького

                              "Сталося  деякій людині до стіни сходи

                               прибрати, стіни ж тієї висота була 117

                               стоп. І узяв він драбину  завдовжки  125

                               стоп.

                               І дізнатися він хоче, на скільки стоп, цю

                               драбину  нижнім кінцем від стіни

                                відставити  треба".

 

Розв’язання

ВС²     =    125²  - 117²  =  1936

ВС = 44 стопи

1 стопа =0,3 м

44 х 0,3 = 13,2 (м)      Відповідь.  13,2 м

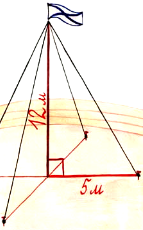
 Задача 2. Для кріплення щогли потрібно встановити 4 троса. Один кінець кожного троса повинен кріпитися на висоті 12 м, інший на землі на відстані 5 м від щогли. Чи вистачить 50 м троса для кріплення щогли, якщо на вузли витратили 10 м ?

Розв’зання

 

 

 (м).

     Задача 3. Задача індійського математика XII ст. Бхаскари.

                             «На березі річки росла самотня тополя.

                                Раптом налетівші вітри зламали її

                              стовбур.

                              Бідна тополя впала, утворивши  кут між

                              стовбуром і поверхнею води річки.

                              Запам'ятай тепер, що в цьому місці річка

                              У чотири лише фута була шириною.

                               Верхівка зламалася, залишивши всього

                               три фути від усього стовбура.

                              Прошу тебе, швидше  мені скажи:

                              Яка висота  тополі?»

 (1фут = 0,3м.)

 (футів).

CD=0,3∙8=2,4 (м).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Лабораторне дослідження.

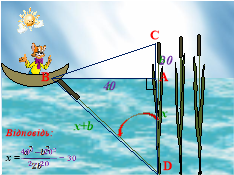
Ви пливете в човні по озеру і хочете дізнатись його глибину. Чи можливо для цього скористатися очеретом, що виглядає із води, не вириваючи його?

Розв’язування.

 Злегка відхиливши очерет і тримаючи його в натягнутому стані, заміряємо відстань а між точками А і В, в яких очерет перетинає поверхню води відповідно у вертикальному і нахиленому положенні. Повернемо очерет в початковий стан і визначимо висоту b над водою, на яку підніметься при цьому точка В нахиленого очерету, зайнявши початкове положення С. Тоді, позначивши через D основу очерету, а через х - шукану глибину АD, з прямокутного трикутника АВD знаходимо  невідомі сторони за теоремою Піфагора,

 

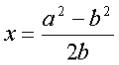звідки      і  

 

Розвязування   прикладних  задач.

Задача.Парк має форму прямокутника. Довжина однієї з його сторін дорівнює 200 м, а площа — 72 000 м². Яка довжина головної алеї парку, що проходить по його діагоналі (рис. 6).

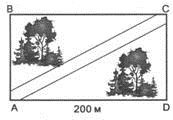
Рис. 6

Розв’зання

 (м).

 м

Відповідь. 411,83 м.

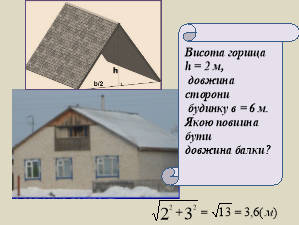
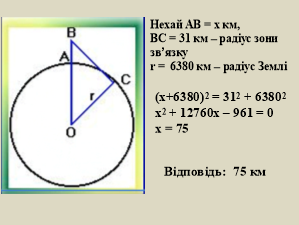
     Задача.  Космонавт під час польоту знаходиться на відстані 327 км над землею. На якій відстані від корабля знаходились у цей час найбільш віддалені від нього видимі ділянки поверхні Землі (рис.7)? (Радіус Землі ≈ 6400 км.)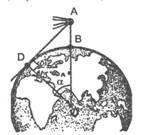                        

 

Рис. 7

Розв’язання

АО=АВ+ВО=327+6400=6727 (км).

 (км).

     Відповідь. 2071,84 км.

     Задача.. Діаметр колоди дорівнює 12 см. Чи можна з цієї колоди витесати квадратний брус із ребром:

а) 10 см; б) 8 см?

Розв'язання

 

 

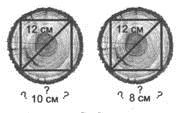
а)  (см).

б)  (см).

     Відповідь. а) Ні; б) так.

 

Підсумок.

«У геометрії є два скарби: перший – теорема Піфагора, другий – золотий поділ. Перший можна порівняти з мірою золота, другий – із коштовним каменем».

(німецький вчений Йоганн Кеплер)

 

 

В «Золотих віршах» Піфагор показав ті моральні правила, суворе виконання яких призводить до ідеалу. Ось декілька з них:

*                Роби тільки те, що не засмутить тебе і не примусить розкаюватись.

*                Навчись тому, що слід знати.

*                Не нехтуй здоров’ям свого тіла.

*                Привчайся жити просто і без розкошів.

*                Не закривай очей тоді, коли хочеш спати, не розібравши всіх своїх вчинків за минулий

   На персні Піфагора було викарбувано 

    такий девіз:  «Тимчасова невдача краща

                                      тимчасової удачі».

Дом. завдання.  ТЕСТ

Вам іти у світ, вам доводити не одну математичну і не одну життєву теорему. Можливо, з часом теорема Піфагора буде здаватися вам дуже простою. Але сьогодні ви подолали певний рубіж, ви стали розумнішими на цілу теорему – на теорему Піфагора, цікаву, могутню і вічну!

 

Вправа „Мікрофон”.

Що нового  дізнались на уроці?

Як читається теорема Піфагора?

Що корисного для себе ви винесли з уроку?

Де, у яких ситуаціях ви можете використати набутий на уроці досвід?

Що ви очікували від уроку? чи збулися ваші очікування?

Самооцінка учнів:1.Я вносив(ла) свої пропозиції…       2.Я активно працював(ла)…

3.Я узагальнював(ла) думки інших…

4.Я був(ла) пасивний(а)…

5. Я не отримав(ла) задоволення від власної праці...