Урок № 6

Тема уроку: Узагальнюючий урок з теми середовище ТЕХ.

Навчальна мета. Узагальнити ЗУН учнів з теми, підготувати учнів до тематичної контрольної роботи; розвивати мислення, пам'ять, швидкість виконання операцій на комп’ютері, інтерес до інформатики; виховувати культуру користувача ПК.

Виховна мета. Виховувати в учнів уважність та відповідальність при виконанні завдань при створенні документа.      

Розвивальна мета. Розвивати творчі здібності та логічне мислення учнів при виконанні завдань.

Тип уроку: комбінований

Хід уроку:

І. Актуалізація опорних знань учнів – фронтальне опитування "Для чого ця команда?" (учням необхідно пояснити призначення певної команди ТП):

1. \documentstyle

2. \bf

3. \it

4. \sqrt

5. \log

6. \frac{25}{36}

7. \alpha, \delta, \zeta, \varthet

8. \int

9. \sum_{k=1}^n

10. \overline

11. \limits

ІІ. Систематизація та узагальнення вивченого матеріалу з теми – виконання практичних завдань на комп’ютерах:

Завдання 1

Наберіть свою біографію  в середовищі ТЕХ.

Завдання 2

Наберіть формули:

.

,

.

;

;

-

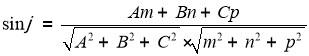
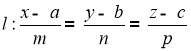
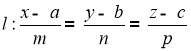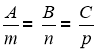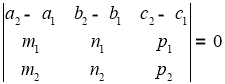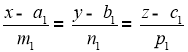і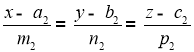

, .

.

.

.

.

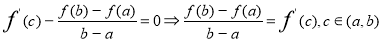Завдання 3

Набрати текст з формулами.

Нехай є гомоморфізмом групи на групу і .Тоді група ізоморфна фактор-групі , причому існує такий ізоморфізм фактор-групи на групу ,  що добуток ізоморфізму на природній гомоморфізм є гомоморфізмом .

Доведення.Задамо відповідність із фактор-групи в групу , вважаючи, що для всякого .

Оскільки для будь-якого то з випливає. Що , тобто і тому відповідність є відображенням в групу . Відображення – інєктивно.

Справді, з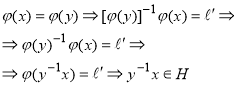

І тому .Очевидно, також, що відображення -сурєктивне. Нарешті, для будь-яких ііз .

.

Отже, є ізоморфізмом в групу .Розглянемо відображення .Оскільки - природній гомоморфізм групи на фоктор-групу , а є ізоморфізмом в групу то , очевидно є відображенням групи на групу . Доведемо, що . Нехай -довільний елемент групи . За означенням природного гомоморфізму, , і, за означенням ізоморфізму, .Отже, , тобто.Таким чином, .Це й означає, що .

Завдання 4

 В середовищі ТЕХ зробити при малюнка (за вибором).

ІІІ. Домашнє завдання: підготуватися до тематичної контрольної роботи.