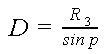Урок 8 Визначення маси і розмірів небесних тіл
11клас
Урок 8
Визначення маси і розмірів небесних тіл
Мета уроку:
навчальна:
- сформувати знання учнів різні способи визначення маси і розмірів небесних тіл;
розвивальна:
- розвивати критичне мислення;
- розвивати предметну компетентність та міжпредметні зв’язки.
виховна:
- сприяти формуванню світоглядних ідей про пізнаванність світу;
- виховувати свідоме ставлення до вивчення предмету, здійснювати патріотичне виховання.
Тип уроку: комбінований
Хід уроку
У всіх областях природи ...
панує певна закономірність,
незалежна від існування мислячого людства.
/Макс Планк/
І. Організаційний момент
II. Повторення та перевірка знань учнів
Диктант
- Учений, основоположник геліоцентричної системи світу (М. Коперник)
- Найближча точка орбіти. (Перигей)
- Значення 149600000км відповідає … (1 а. о.=149600000км )
- Основні закони небесної механіки. (ЗВТ, закони Кеплера)
- В якій точці еліптичної орбіти найменша швидкість? (В апогеї)
- Німецький астроном, який відкрив закони руху планет (Й. Кеплер)
- Формула третього закону Кеплера.
- Відношення квадратів періодів обертання двох планет дорівнює 8. Чому дорівнює відношення їх великих півосей.(2)
- У якій конфігурації на мінімальну відстань до Землі підходить нижня планета? ( У нижньому сполученні)
- У якій конфігурації на мінімальну відстань до Землі підходить верхня планета? (У протистоянні)
- Які планети можуть проходити по диску Сонця? (Меркурій, Венера)
III. Мотивація навчальної діяльності. Формулювання теми і завдань уроку
ІV. Вивчення нового матеріалу
Визначення розмірів, мас небесних тіл і відстаней до них у Сонячній системі.
Визначення відстаней методом горизонтального паралаксу.
Середню відстань від усіх планет до Сонця в астрономічних одиницях можна обчислити, використовуючи третій закон Кеплера. Із 40-их рр. ХХ ст. радіотехніка дала змогу визначити відстані до небесних тіл за допомогою радіолокації. Та класичним способом визначення відстаней був і залишається кутомірний геометричний спосіб. Ним визначають відстані й до далеких зір, до яких метод радіолокації застосувати неможливо. Геометричний метод ґрунтується на явищі паралактичного зміщення.
Паралактичне зміщення (паралакс світила) - удаване зміщення світила, обумовлене переміщенням спостерігача. Визначення відстаней до тіл Сонячної системи ґрунтується на вимірюванні їхніх горизонтальних паралаксів.
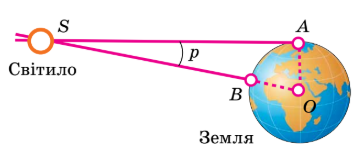
Кут р, під яким зі світила видно радіус Землі, перпендикулярний до променя зору, називають горизонтальним паралаксом.
Знаючи горизонтальний паралакс світила, можна визначити його відстань D=SO від центра Землі.
|
Визначення відстані до світила методом горизонтального паралаксу: |
|
|
де |
Мал. Що більша відстань до світила, то менший кут р. |
Прийнявши ![]() за одиницю, можна виразити відстань до світила в земних радіусах. Наприклад, паралакс Сонця
за одиницю, можна виразити відстань до світила в земних радіусах. Наприклад, паралакс Сонця ![]() . Паралаксу Сонця відповідає середня відстань від Землі до Сонця, приблизно 149,6 млн. км. Цю відстань приймають за одну астрономічну одиницю (1 а.о.).
. Паралаксу Сонця відповідає середня відстань від Землі до Сонця, приблизно 149,6 млн. км. Цю відстань приймають за одну астрономічну одиницю (1 а.о.).
В астрономічних одиницях зручно вимірювати відстані між тілами Сонячної системи.
При малих кутах ![]() , якщо кут виражений в радіанах. Якщо р виражено в секундах дуги, то вводиться множник
, якщо кут виражений в радіанах. Якщо р виражено в секундах дуги, то вводиться множник ![]() , де 206265 - число секунд в одному радіані. Тоді
, де 206265 - число секунд в одному радіані. Тоді ![]() і
і ![]() . Це рівняння значно спрощує обчислення відстані D до світила за відомим паралаксом р.
. Це рівняння значно спрощує обчислення відстані D до світила за відомим паралаксом р.
Під час спостереження небесних тіл Сонячної системи можна виміряти кут, під яким їх видно спостерігачеві із Землі. Знаючи кутовий радіус ![]() об’єкта і відстань D до об’єкта, можна обчислити лінійний радіус R цього об’єкта за формулою:
об’єкта і відстань D до об’єкта, можна обчислити лінійний радіус R цього об’єкта за формулою: ![]() .
.
|
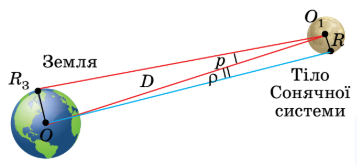
Визначення лінійних розмірів тіл Сонячної системи: |
|
|
|
|
За визначенням горизонтального паралакса, радіус землі видно зі світила під кутом р, тоді одержимо: ![]() . Оскільки значення кутів
. Оскільки значення кутів ![]() і р малі, остаточно маємо:
і р малі, остаточно маємо: ![]() . Визначити розміри небесних тіл таким способом можна тільки тоді, коли видно їхні диски.
. Визначити розміри небесних тіл таким способом можна тільки тоді, коли видно їхні диски.
Щоб визначити лінійний розмір небесного тіла, потрібно виміряти кут, під яким ми бачимо його радіус, і знати відстань до нього. На рис. 6.1 спостерігач із центру TЗемлі може бачити лише лінійний радіус R тіла під кутом p.
Відстань від центра Землі до центра небесного тіла позначимо літерою D. Тоді: R = D • sin(p).
Якщо D виразити в радіусах Землі, то й R ми знайдемо в радіусах Землі. Якщо D виразити в кілометрах, то R вийде в кілометрах.
Наприклад, відстань до Місяця D дорівнює 60 земним радіусам, а радіус Місяця ми бачимо під кутом 16'. Для Місяця R = 60 • sin(16') = 0,27 радіуса Землі.
Радіолокаційний метод.
Для визначення відстаней до тіл Сонячної системи використовують найбільш точні методи вимірювання - радіолокаційні вимірювання.
|
Мал. Радіолокаційна станція |
Мал. Принцип роботи радіолокаційної станції |
Вимірявши час t, потрібний для того, щоб радіолокаційний імпульс досяг небесного тіла, відбився і повернувся на Землю, визначають відстань D до цього тіла за формулою![]() .
.
|
Визначення відстані до тіл Сонячної системи радіолокаційним методом: |
де |
За допомогою радіолокації визначено найбільш точні значення відстаней до тіл Сонячної системи, уточнено відстані між материками Землі, більш точно визначено астрономічну одиницю. Методи лазерної локації (наприклад, спеціальні кутові відбивачі, доставлені на Місяць) дали змогу виміряти відстань від Землі до Місяця з точністю до кількох сантиметрів.
На тіло масою m, яке розташоване поблизу поверхні Землі, діє сила тяжіння F = mg, де g — прискорення вільного падіння. Якщо тіло рухається лише під дією сили тяжіння, то застосовують закон всесвітнього тяжіння. Прискорення вільного падіння, спрямоване до центру Землі, обчислюють за формулою:
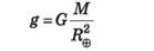 (1)
(1)
Отже, знаючи, що прискорення вільного падіння g= 9,81 м/с2, G= 6,673 • 10-11 Η·• м2/кг2 і радіус Землі R⊕= 6370 км, можна за формулою (2) обчислити масу Землі (3).
 (2)
(2)
M = 5,97 • 1024 кг (3)



V. Закріплення вивченого матеріалу
1. Запитання 1,2 (§6.)
2. Задача. Чому дорівнює лінійний діаметр Місяця, якщо його видно з відстані 400000 км під кутом 0, 5°?
3. Задача. Визначте період обертання Марса навколо Сонця, якщо його протистояння відбуваються кожні 780 діб.
4. Задача. Визначте відстань від Сонця до Урана, якщо період обертання Урана навколо Сонця 84 роки.
Вправа «Сьогодні на уроці я…»
- навчився…,
- переконався…,
- зрозумів…,
- зумів…,
- зробив для себе висновок…, і т.д.
VIІ. Домашнє завдання
1. Опрацювати тему 1
Для допитливих
В астрофізиці одиницею для вираження й порівняння мас зір та інших астрономічних об’єктів (зокрема, галактик) є маса Сонця. Вона позначається через М☉ і дорівнює масі Сонця: М☉ = (1,98847 ± 0,00007) • 1030 кг.
Сонячна маса перевищує масу Землі майже в 332 946 разів. Близько 99,86% маси Сонячної системи припадає саме на Сонце, а загальна маса усіх планет становить лише 0,0013 М☉,причому більша частина сумарної маси планет належить Юпітеру (його маса у 1047,56 разів менша за сонячну).
Маса більшості окремих зір у Всесвіті складає від 0,08 до 50 М☉, а маса чорних дір і цілих галактик може сягати мільйонів і мільярдів мас нашого світила.
-
-
-
Дякую за розробку!


про публікацію авторської розробки
Додати розробку