Урок алгебри 8 клас. " Відсотки в задачах бізнесово - фінансового змісту".

«Нажити багато грошей – хоробрість,

  зберегти їх – мудрість,

  а уміло витратити – мистецтво.»

Б.Авербах

Тема уроку.  Відсотки в задачах  бізнесово-фінансового змісту

 

Мета уроку: навчальна: узагальнити і систематизувати знання учнів про відсотки: запис відсотків у вигляді дробу, запис числа у вигляді відсотків, знаходження відсотка від числа, числа за його відсотком, відсоткового відношення;

розвивальна: розвивати в учнів усний рахунок, обчислювальні навички, логічне мислення творчість, збагачувати математичну мову;

виховна: виховувати інтерес до предмета, любов до прекрасного.

Тип уроку. Узагальнення і систематизації знань.

Обладнання. Картки – завдання, ілюстрації.

Хід уроку

 І. Організаційно  психологічний  етап.

          Учитель  читає  епіграф  уроку ,  який  написано  на  дошці.

-  Вітаю  вас!  Запам’ятайте  цей  день  і  цей  вислів,  бо  можливо  через  кілька  років  під час  урочистої  прес-конференції   молодий  допитливий  журналіст  запитає  вас: „ Шановний .........,  а  з  чого  розпочався  ваш  фінансовий  шлях?  Як  ви  досягли  такого  успіху?”.  А  ви  й  скажете:  „Все  почалось  з  уроків  математики.  Мені  допомогло  знайомство  із  курсом  задач  економічного  змісту,  яке  розпочалось  із  славетних  слів  Авербаха.”

- Діти,  нажаль  я  не  зможу  навчити  вас,  як  „ нажити  багато  грошей”,  але  я  дуже  хочу  підказати  вам,  як  їх  уміло  зберегти  чи  витратити,  щоб  ви,  ваша  родина  і  наша  держава  в цілому  крок  за  кроком  прямували  до  фінансового  успіху!

Цьому  можна  навчитися,  якщо  розумно  використовувати  свої  знання!  І  у першу  чергу  знання  з  математики!

ІІ. Мотивація навчальної діяльності.

     -„ Доросле  життя”  ставить  перед  кожним  з  нас  багато  питань.   Як  ви  гадаєте,  які  питання  ставить  життя  перед  дорослою  людиною?

Можливі  варіанти  відповідей:  ( учитель  допомагає  дітям )

• чому  є  люди  багаті  й  бідні;
• як  отримувати  велику  заробітну  плату;
• як  зробити  правильний  вибір  або  прийняти  вірне  рішення;
• що  потрібно  для  здійснення  бажань;
• чому  краще  жити  сім’ями;
• як  здійснити  вірну  покупку  тощо.

    -  На  безліч  подібних  питань  вам  дасть  відповіді  чарівна  наука – економіка,  яку ви  почнете  серйозно вивчати  у  старших  класах.  Але  деякі  економічні  проблеми  ми  можемо  розглянути  вже  у  шостому  класі ,  бо  рівень  нашої  математичної  компетентності  дозволяє  нам  розв’язувати  задачі  економічного  змісту.

        Скажіть,  які  асоціації  викликає  у  вас  словосполучення  „задачі  економічного  змісту”?  Як  ви  гадаєте,  якою  буде  тематика  задач  сьогоднішнього  уроку?

                                   Складається  „асоціативний  кущ”:

 

 

 

 

 

 

Можливі  варіанти  відповідей:

• гроші, банки;
• вклади, відсотки;
• борги,  прибутки;
•  майно;
• підприємства,  підприємці  тощо.

Учитель  підводить  підсумки,  узагальнює  відповіді  дітей.  Висновок:  сьогодні,  як  ніколи,  ми  побачимо, що  мета  нашої  роботи  не  в  тому,  щоб  розв’язати  якусь  задачу  ( одержати  відповідь ),  а  в  тім,  щоб  одержати  від  цієї  задачі  користь.

 

           ІІІ. Актуалізація опорних знань і вмінь.

Метод «Мікрофон»

1. Що таке відсоток? Як інакше називають відсотки?
2. Як записати відсотки у вигляді числа? 5%, 17%, 300%
3. Як записати число у вигляді відсотка? 0,09; 0,34; 1,6; 8.
4. Що означає збільшити число на 100%?
5. Що означає зменшити число на 50%? 
6. Який зв’язок між найпростішими значеннями відсотків і відповідними дробами? (ціле – 100%, половина – 50%, чверть – 25%, п’ята частина – 20%, три чверті -  75%, дві п’ятих – 40%)
7. Які є типи задач на відсотки?
8.  Як знайти р відсотків від числа а?
9. Як знайти число, р% якого дорівнюють с?
10.  Як знайти відсоткове відношення?

Усний рахунок.( на дошці)

1.               Знайти 1 % від 80кг. ( 0,8кг)
2.               знайти 10 % від 150 грн. (15 грн)
3.               Знайти 15 % від 100кг. (15кг)
4.               Знайти 50 % від 120 т. (60 т)
5.               Знайти 25 % від 40га. (10га)
6.               Знайти 20 % від 800 грн. ( 160 грн)
7.               Скільки гривень одержить клієнт банку від 100 грн, якщо банк виплачує 25 % річних.  (125 грн)
8.               На скільки відсотків збільшилася кількість учнів, що вчаться на 7 – 9 балів, якщо: а)в першому семестрі їх було 8, а в другому стало 12 учнів; б) було 8, а стало 10? (50%, 25%)
9.               На скільки відсотків знизилась вартість товару, якщо він коштував 100 грн, а тепер коштує 85 грн? (15%)

IV.Розв’язування задач на повторення

1. Магазин отримав книжку за 55,50 грн., націнка магазину 20%. При оптовій закупці магазин зменшив свою ціну на 5%. Скільки коштує така книжка при оптовій закупці?

Розв’язання.

1. 55,5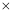0,2=11,1(грн.)
2. 55,5+11,1=66,6(грн.)
3. 66,6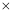0,05=3,33(грн.)
4. 66,6-3,33=62,27(грн.) коштує книжка при оптовій закупці.

Відповідь: 62,27 грн.

2. Узимку куртка коштувала 1600 грн., навесні ціна на неї знизилась на 15 %. Яка ціна куртки навесні?  Розв’язання:

100%-1600 грн.

15%-х грн.

Х==240 (грн.)

1600-240=1360 грн.

Відповідь 1360 грн.

3. Службовець сплачує медичну страховку у розмірі 1200 грн., що становить 15 % його заробітної плати. Яка заробітна плата у службовця?

Розв’язання.

1200 грн – 15%

х грн. - 100%

Відповідь: 8000 грн.

4. За деяку роботу робітникові нарахували 2395 грн. Із них

13 % - прибутковий податок,

2 % - відрахування у пенсійний фонд,

1 % - відрахування у фонд зайнятості,

1 % - профспілковий внесок.

Скільки одержить працівник після всіх відрахувань?

Розв’язання.

13+2+1+1=17%

100%-17%=83%

2 395 грн – 100%

х грн – 83%

грн

Відповідь: працівник одержить 1987,85 грн.

 Де застосовуються відсотки? Людям яких професій потрібно вміти розв’язувати задачі на відсотки? ( доповіді учнів)

V. Систематизація навчальних досягнень (вмінь і навичок).

Завдання класу: Розв’яжи завдання, запиши букви, що відповідають правильним відповідям. З отриманих букв склади слово.

1. Вартість товару збільшилася на 50%. В скільки раз зросла вартість товару?

 

              5 разів;                             1,5 рази;                           150 раз. 

 

2. Від якого числа 40 складає 25%?

 

              160;                                   80;                                      120. 

 

3. Число 60 збільшили на 20% від 60. Яке число одержали?

 

              94;                                     82;                                     72.

 

4. Вартість товару збільшилася в 2 рази. На скільки відсотків збільшилася вартість товару?

 

              100%;                                200%;                                50%.

 

5. Банк виплачує вкладникам кожного місяця 2% від внесеної суми грошей. Вкладник поклав на рахунок 200 гривень. Яка сума буде на його рахунку через півроку?

 

              226 грв;                            224 грв;                             324 грв.

 

 Яке слово ми отримали? Надія - так називається наш банк. Я в свою чергу теж маю надію, що сьогоднішній урок буде корисним для вас і ми отримаємо взаємне задоволення від нашої співпраці.

      Отже, кожен з вас зараз зробив грошовий внесок на рахунок банку, або на депозит, і тепер, панове акціонери, нам цікаво, а скільки грошей прибутку ми можемо отримати за збереження вкладених грошей?

Розглянемо задачу:

Банк „Надія” за збереження грошей на довгостроковому вкладі виплачує 20% річних, з урахуванням того, що ця сума не буде братися клієнтом протягом усього терміну. Скільки грошей одержить клієнт банку через 2 роки, якщо він спочатку року вклав 1000 гривень?» (на другий рік відсотки нараховуються із суми, що вийшла наприкінці попереднього року).

  - Складіть вираз до задачі: – на кінець першого року;

+ ( )  0,2 – на кінець другого року;

1200 + 240  = 1440 (грн)

Індивідуальна робота:

– А тепер складіть вираз до задачі і обчисліть, яка сума буде на рахунку через 5 років.

Виявлення причини утруднення і постановка мети діяльності.

– Чому ви не змогли розв’язати  задачу, адже з аналогічною, попередньою задачею ви справилися? (У попередній задачі термін, зазначений в задачі був невеликий, а в цій задачі 5 років, прийдеться довго розв’язувати  цю задачу)

– Як ви думаєте, що ж нам робити? (Знайти швидкий спосіб розв’язання  таких задач).

 

– формула простого відсоткового зростання.

S – сума, внесена в банк;

р – відсоток, який сплачує банк щомісяця вкладникові від внесеної суми;

n – кількість місяців;

– сума, яка буде на рахунку через n місяців.

– формула складних відсотків, або закон                                               накопичення грошей.

VI. Самостійна робота із самоперевіркою по еталону.

   У банку „Надія” оголошується конкурс на заміщення вакантних посад: економіста, бухгалтера, бізнес аналітика, банкіра. В залежності від того, який рівень задач ви в змозі розв’язати, таку посаду і можете отримати.

№ 1 (для слабо встигаючих учнів) (на 7 балів)

Яка сума буде на рахунку через 3 роки, якщо на нього поклали 2000 гривень під 30% річних?

Еталон:

(1 + 0,3)³  2000 = 1,3³  2000 = 2,197  2000 = 4394 (грв.)

 

№ 2 (для учнів із середніми здібностями) (на 9 балів)

Початковий вклад клієнта банку становить 5000 гривень. Річна відсоткова ставка банку 20%. Яким стане вклад через 3 роки, якщо:

а) банк нараховує прості відсотки;

б) банк нараховує складні відсотки?

Еталон:

При простому відсотковому зрості через 3 роки сума складає: = 8 000 (грн);

При складному відсотковому зрості: 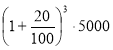= 1,728 * 5000 = 8640 (грв).

№ 3 (для учнів з високим рівнем знань) (на 11 балів)

 Через 2 роки знаходження грошей в банку, вкладник одержав 14 520 гривень при нарахуванні 10% річних. Яку суму поклав вкладник два роки тому?

Еталон:

(1 + 0,1)²  S = 14 520;

(1,1)²  S = 14 520;

1,21S = 14 520;

S = 14 520 : 1,21;

S = 1 452 000 : 121;

S = 12 000.                Відповідь: вкладник поклав 12 000 гривень.

 

      Учні самостійно перевіряють виконану роботу, звіряючись з еталоном, виправляють помилки.

- А тепер я допоможу вам з’ясувати, ким ви можете працювати у нашому банку.

Якщо ви отримали від 6 – 7 балів, то бухгалтером.

Якщо ви отримали 8 – 9 балів, то економістом.

Якщо ви отримали 10 балів, то бізнес аналітиком.

Якщо ви отримали 11 балів, то банкіром.

 

 

 

VII. Включення в систему знань і повторення.

 

№ 1. Через 3 роки знаходження грошей в банку, вкладник  одержав 10 000 карбованців при нарахуванні 20% річних. Яку суму поклав вкладник два роки тому?

 (1 + 0,2)³  S = 10 000;

(1,2)³  S = 10 000;

1,728S = 10 000;   S = 10 000 : 1,728;

S  5787;   S  5800    

Відповідь: треба покласти 5800 гривень.

№ 2. Говорять, що в 1723 році гетьман Полуботок поклав до англійського банку великий капітал з України під 4 % річних. У скільки разів збільшився б той капітал до наших днів?

(1 + 0,04)²⁸⁷ = 1,04²⁸⁷ =

Додаткова задача.

Одного разу, розв’язуючи домашнє завдання, син власника нафтової компанії випадково вліз у систему ціноутворення і знизив ціну на гас, який коштував 2000 грн. за тонну, на 10%. Коли це з’ясувалося, перед компанією постала проблема. На скільки відсотків потрібно підняти нову ціну, щоб отримати початкову?

Початкова ціна (2000 грн.) становить 100%, а знижена ...

100% - 10%   .... 90%. Знижена ціна становить 90% від початкової.

Нехай ціна після зниження дорівнює х грн.

Тоді:

2000 грн. — це 100%;

х грн. — 90%.

х = 90% ∙ 2000 і поділити на 100%.

х = 1800.

Отже, знижена ціна – 1800 грн/т.

Щоб знайти, на скільки відсотків потрібно підняти нову ціну, щоб отримати початкову, порівняємо з новою ціною (1800 грн.) стару. Нова ціна становить 100 відсотків, а початкова ціна (2000 грн.) - х відсотків від нової. Тоді:

1800 грн. — це 100%;

2000 грн. — х%.

х = 2000∙100% і поділити на 1800 =  відсотка.

Отже, нову ціну слід підняти на %.

 

 

 

VIII. Рефлексія діяльності.

«Закінчіть прислів'я»

1. Зароблена копійка краща за крадений…(Карбованець)

2. Не взявшись за сокиру, хати не… (Зробиш)

3.Боржник коли бере – плаче, а віддає…(Скаче)

4. У базарі два дурні: один дешево дає, другий дорого …(Просить)

5. Дорого – не дорого, а поторгуватися …(Треба)

6. Достаток чинить…(Статок)

7.Від прибутку голова не …(Болить)

8. Загубив – смутися, знайшов – не …(Веселися)

9 Грошей кури не …(Клюють)

10 Гроші – сила: одних підкуплять, других напоять, а третім лиха …(Накоять)

11. На гривеник покупки, а на карбованець …(Крику)

12. Копійка гривню…(Береже)

13. З чужої кишені платити …(Легше)

14. Бачили очі, що …(Купували)

15. З розумом торгувати, а без розуму …(Бідувати)

16. Що не продаси, то так …(Даси)

17. На дешеве шкода …(Грошей)

18. Аби добрий товар, а купець …(Знайдеться)