Урок для 8 класу "Квадратні рівняння. Неповні квадратні рівняння" + презентація

План – конспект уроку (8 клас)

з алгебри

Вчитель Демченко Н.В.

Тема: Квадратні рівняння. Неповні ква­дратні рівняння

Мета:

загальноосвітня:

- ввести означення квадратного рівняння та поняття неповного квадратного рівняння;

- формувати вміння розв’язувати неповні квадратні рівняння;

виховна і розвиваюча:

•                   розвиток пізнавальних інтересів та інтересу до предмету;
•                   виховання інформаційної культури учнів;
•                   виховання уважності , акуратності , дисциплінованості ;
•                   прищеплення навичок самостійної роботи;
•                   формування вміння вести дискусію.

Завдання уроку:

•                   навчитися розпізнавати квадратні рівняння серед інших рівнянь;
•                   навчитися визначати коефіцієнти в квадратному рівнянні;
•                   знати означення квадратного рівняння;
•                   уміти розв’язувати неповні квадратні рівняння.

Обладнання: дошка, крейда, комп’ютер, проектор, Г.П.Бевз  Алгебра: підручник для 8 класу.

Тип уроку: урок засвоєння нових знань.

Хід уроку

І.Організаційний момент

 Перевірка наявності учнів в класі та їх готовності до уроку.

- Діти, сьогодні на уроці у нас присутні гості, давайте привітаємо їх.

- Сьогодні тема нашого уроку «Означення квадратного рівняння. Неповні квадратні рівняння». Тему запишемо в зошит. (Слайд 1).

ІІ. Вступне слово вчителя

Загадкове, нам знайоме,

В ньому є щось невідоме.

Його треба розв’язати,

Тобто корінь відшукати.

Кожен легко, без вагання

Відповість, що це - …

                           (Рівняння) (Слайд 2)

На цьому уроці ми з вами повинні засвоїти зміст понять «квадратне рівняння», «неповне квадратне рівняння» та навчитися розв’язувати неповні квадратні рівняння.

Завданнями нашого уроку будуть:

•                   навчитися розпізнавати квадратні рівняння серед інших рівнянь;
•                   навчитися визначати коефіцієнти в квадратному рівнянні;
•                   навчитися пояснювати сенс поняття «квадратного рівняння»;
•                   навчитися розв’язувати неповні квадратні рівняння. (Слайд 3)

Історична довідка                                                                      

Квадратні рівняння простіших видів вавилонські математики вміли розв’язувати ще 4 тис. років тому. Згодом розв’язували їх також в Китаї та Греції. Особливо багато уваги квадратним рівнянням приділив Мухамед аль-Хорезмі (ІХ ст.). (Слайд4)

ІІІ. Актуалізація опорних заннь

Задача. Одне з двох чисел більше від другого на 2, а їх добуток дорівнює 35. Знайти ці числа. (Слайд 5)

                                         Розв’язання:

    Позначимо менше число через х. Тоді більше число буде дорівнювати х+2. Їх добуток 35. Маємо рівняння:

х(х+2)=35:

  х² + 2х - 35=0.

 Це - рівняння другого степеня з однією зміною.

 Такі рівняння називаються квадратними.

ІV. Засвоєння нових знань

Означення квадратного рівняння:

Квадратним називають рівняння виду

                             ах²+вх+с=0,

де х - змінна, а а, в, с – дані числа, причому а ≠ 0. (Слайд 6)

           Яке з даних рівнянь квадратне:

         а) 5х²+3х+4=0;                 б)х² -3х=0;

 в) – х² +4х+3=0;                г) 6х+5=0;                       

е) 7у(у+1)=2;              ж)0х² +5х-2=0. (Слайд7)           

Числа a, b, c  - називаються   коефіцієнтами квадратного  рівняння

                                       а – перший коефіцієнт;

b – другий коефіцієнт;

с – вільний член (Слайд 8)

Завдання                                                                                          

Назвіть коефіцієнти квадратних рівнянь:

а) 7х² - 3х + 4=0;           г)-2х² + 8х=0;

б) 2х² + х -10=0;            д)16х² - 4=0;

в) - х² - 5х + 6=0;           е)3х² =0. (Слайд 9)

Квадратне рівняння називається з в е д е н и м ,

 якщо його перший коефіцієнт дорівнює одиниці (а = 1) (Слайд 10)

Яке з наведених квадратних рівнянь є зведеним : (Слайд 11)

Якщо у квадратному рівнянні хоча б один із коефіцієнтів      або 

дорівнює нулю     (b = 0,  c = 0),

то таке рівняння називається  неповним квадратним рівнянням (Слайд 12)

Неповні квадратні рівняння

1.               ах² = 0;
2.               ах²  + вх = 0;
3.               ах²  + с = 0. (Слайд 13)

Яке з рівнянь є неповним квадратним?

 а) х² +4=0;          б) 5х² =0; 

         в) х² -2х=0;         г) 3х² + 2 х-1 =0;

         д) 6х² +3х+2=0;       е) 4х² -2х=0. (Слайд 14)

Розглянемо рівняння виду ах² = 0. (Слайд 15)

Якщо а ≠ 0, в = 0, с = 0, то ах² + 0х + 0= 0, тоді  ах² = 0,

                            Розв’язання :

                  х = 0 єдиний корінь.

Рівняння виду ах² +вх=0 (Слайд 16)

Якщо а ≠ 0, в ≠ 0, с = 0, то

ах² + вх + 0 = 0;

ах² + вх = 0;

х(ах + в) = 0;

х=0  або  ах = -в;

  х  = - в/а

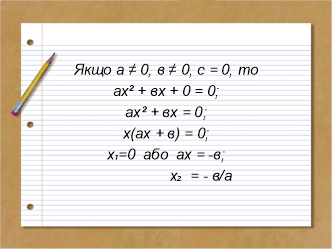
Розв’язати рівняння (Слайд 17)

а)4х² +8х=0;                              б) -5х² +15х=0; 

4х(х+2)=0;                                     -5 х(х-3)=0;

4х=0, х+2=0;                                 -5х=0, х-3=0;

  х=0,  х=-2.                                      х=0,  х=3.

Відповідь: -2; 0                            Відповідь:  0; 3

Рівняння виду ах² + с = 0 (Слайд 18)

Якщо а ≠ 0, в = 0, с ≠ 0, то  ах² + 0х + с=0

                                                ах² +с=0

                                                ах² = - с

                                                х² = -

Якщо - 0, то                                           Якщо - ˂ 0, то дійсних                                                                                          

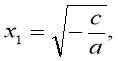
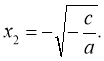                                                                      коренів немає

Розв’язати рівняння (Слайд 19)

а)4х² +16=0;                                                 б)3х² - 48=0;

4х²= - 16;                                                           3х² =48;

  х² = - 4;                                                             х² =16;

 - 4 <0 ;                                                               16 ≥0 ;

  коренів немає;                                               х₁ = -4,      х₂ = 4.

Відповідь: коренів немає.             Відповідь: -4; 4.                     

ІV. Відпрацювання навичків розв’язування неповних квадратних рівнянь

Завдання (Слайд 20)

Замініть дане рівняння рівносильним йому квадратним рівнянням:

а) (х-1)(х-2) = 4х;     б) 3(х+5) – 8 = - 5х(х+2).

Робота з підручником. (Слайд 21)

№870

 а)16х²=0;                 б) -4у²=0.

№871

 б) 2х² - 8х =0 ;             г) х = х².

№872

 б)-2х² + 50 = 0;                в)9х² = 64.

№877

 б) 2(х² - 1)=(х – 1)(х + 1).

V. Підсумок уроку (Слайд 22)

•                  Сформулюйте означення повного квадратного рівняння
•                  У рівнянні 3х²-7х+2=0 назвіть коефіцієнти а, в, с.
•                  Запишіть рівняння, якщо в=0, а=-1, с=2.
•                  Як називається таке рівняння?
•                  Скільки коренів мають рівняння ах²=0, ах²+вх=0, ах²+с=0?

VІ. Домашнє завдання (Слайд 23)

§19,  №869(а,б), №873(а,в), №876(А), №886(Б)