Урок алгебри (8 клас) з теми: "Розв'язування рівнянь, що зводяться до квадратних"
Урок алгебри (8 клас) з теми: "Розв'язування рівнянь, що зводяться до квадратних".
Урок узагальнення та систематизації знань й умінь учнів
Урок: «Розв’язування рівнянь, що зводяться до квадратних»
Формування компетентностей:
- предметна компетентність: узагальнити і систематизувати відомості про квадратні рівняння; зорієнтувати учнів на знаходження різноманітних шляхів розв’язку більш складних рівнянь, застосовуючи опорні знання і навички учнів;
- ключові компетентності:
- спілкування державною мовою – грамотно використовувати рідну мову, з розумінням застосовувати математичні терміни;
- уміння вчитись впродовж життя – вдосконалювати результати своєї діяльності, підвищувати інтерес до вивчення математики, спираючись під час уроку на емоційні ситуації відкриття нового, підключаючи яскраві приклади і факти із життя вчених-математиків;
- ініціативність і підприємливість – аргументовано відстоювати свою точку зору, оптимізувати способи розв’язання завдання;
- соціальна та громадянська: співпрацювати в команді, усвідомлювати власну роль в роботі команди; вчитись помічати красу оточуючої природи рідного краю.
Обладнання: ноутбук, проектор; портрети Ф. Вієта, Аль-Хорезмі, плакат із висловом Г. Лейбніца: «Хто хоче обмежитися теперішнім без знання минулого, той ніколи його не зрозуміє»; презентації «Історія виникнення та розв’язування квадратних рівнянь», «Франсуа Вієт - видатний математик свого часу», відеоролик до релаксації «Музика природи…»
План-хід уроку
- Перевірка домашнього завдання. Математичний кросворд – систематизація теоретичних знань. Клас ділиться на дві групи – (два учні, по одному від кожної групи, на які поділено клас, розв’язують його на відкидних дошках, решта – на отриманих віддрукованих аркушах).
(Слайд 2). Питання по горизонталі:
- Як називається число, що визначає кількість коренів квадратного рівняння?
- Як називаються числа, що перетворюють рівняння на правильну рівність?
- Як називають рівняння виду ах4 + вх2 + с = 0 ?
- Яка величина за теоремою Вієта, повинна дорівнювати другому коефіцієнту, взятому з протилежним знаком?
- Як називається твердження, яким користуємося при розв’язуванні зведених квадратних рівнянь?
- Як називаються рівняння, в яких числа а, в або с, або вони разом дорівнюють нулю?
- Що треба поміняти у другому коефіцієнті зведеного квадратного рівняння, щоб знайти суму його коренів за теоремою Вієта?
Питання по вертикалі:
- Яка величина за теоремою Вієта, повинна дорівнювати вільному члену?
Команди, обміняйтеся роботами. Виконаємо взаємоперевірку кросворду. 10 балів виставляємо за правильно виконану роботу. Якщо є помилки - підкреслюємо їх, бали не виставляємо. Учні біля дошки теж перевіряють роботи один одного.
Отже, якщо ви правильно розгадали кросворд, то ключове слово по вертикалі – це «добуток».
Підніміть руки ті, хто відповів правильно на всі вісім запитань; сім, шість, п’ять.
Таким чином можна зробити висновок про те, як ви засвоїли теоретичний матеріал з даної теми. Декому треба його доопрацювати.
Вчитель виставляє оцінки учням, що розгадували кросворд на відкидних дошках. Команди повертають роботи одна одній. Перемагає та команда, де більше правильно розгаданих кросвордів.
ІІ. Актуалізація опорних знань учнів.
На дошці записані рівняння:
1). 9х2 = 0; 2). 5х2 = 20х; 3). у2 – 6у + 8 = 0; 4). 2z2 + 9z – 10 = 0; 5). 3х2 + 12 = 0.
Питання учням:
- Які рівняння записані на дошці?
- Що можна про них сказати?
(Записані повні, неповні та зведене квадратне рівняння).
- Перше рівняння – неповне, числа в і с рівні нулю, корінь рівняння х=0;
- друге рівняння – неповне, число с = 0, коренів два х1 = 0; х2 = 4;
-
третє рівняння – зведене, D > 0, за оберненою т. Вієта корені
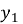 = 2,
= 2,
![]() = 4;
= 4;
-
четверте рівняння – квадратне загального типу; дискримінант і корені знаходяться за формулами D =
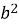 – 4a;
– 4a; 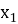
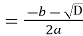 ; ;
; ;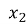
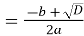 ;
;
-
п’яте рівняння – неповне, число в рівне нулю, коренів рівняння немає, бо 3
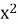 ≠ -12).
≠ -12).
Отже, ми повторили загальні відомості про квадратні рівняння, а чи завжди вони мали такий вигляд і як давно людство розв’язує їх?
На ці питання можна відповісти, якщо не нехтувати наступним висловом Г. Лейбніца: «Хто хоче обмежитися теперішнім без знання минулого, той ніколи його не зрозуміє».
(Переглядаємо презентацію, підготовлену учнями, про історію виникнення і розв’язування квадратних рівнянь). ( Слайд 3-7)
ІІІ. Систематизація навичок учнів у розв’язуванні рівнянь, що зводяться до квадратних.
На дошці обом групам записані рівняння:
1). х - 7![]()
2). ![]()
![]() +
+![]()
3). х +3 = ![]()
4). 2(t - 5)2 + 4(t - 5) – 3 = 0.
Що об’єднує ці рівняння? Так, спосіб розв’язку – всі вони зводяться до квадратних рівнянь.
Пропонується кожній групі учнів розділитися на підгрупи, вибрати і розв’язати по одному із даних рівнянь. Відповіді записати під відповідним рівнянням на дошці.
(Вчитель контролює роботу учнів, перевіряє правильність відповідей, визначає переможців).
Під час роботи учні повторюють алгоритм розв’язку кожного рівняння. Рівняння 1) , 2) і 4) розв’язуються шляхом введення допоміжної змінної.
Отже, всі рівняння, які ми розв’язували до цих пір, зводилися до квадратних.
ІV. Фізкультхвилинка.
V. Застосування набутих навичок у нестандартних умовах.
А як би ви розв’язали наступне рівняння: 3(х2 ![]() – 7(х +
– 7(х + ![]() = 0?
= 0?
(Учні висловлюють свої думки, пропозиції)
Так, і це рівняння можна звести до квадратного, якщо ввести допоміжну змінну, а для цього виразити суму квадратів через квадрат їхньої суми (вчитель працює разом з учнями):
![]() тоді
тоді
![]() =
=![]() -2.
-2.
Маємо: ![]()
![]()
![]() та отримаємо нове рівняння:
та отримаємо нове рівняння:
![]()
(це рівняння розв’язує учень біля дошки)
![]() =
=![]()
![]()
![]() .
.
Далі повертаємось до введеної змінної і ще два учні розв’язують нові рівняння:
|
|
та |
|
|
(коментовано)
|
|
(самостійно) |
|
Немає дійсних коренів. |
|
|
Відповідь:
|
|
|
Таким чином, ми розглянули алгоритм розв’язування більш складного рівняння, зведенням його до квадратного.
А тепер я хочу повернути вас до попередніх трьох рівнянь. Розв’язуючи їх ми приходили до зведених квадратних рівнянь, корені яких знаходили за теоремою Вієта. Ось я і хочу, щоб зараз ви переглянули презентацію про цього видатного математика, якого вдячні колеги назвали «батьком алгебри».
(Слайди 8-13).
VІ. Підсумок уроку.
Отже, на сьогоднішньому уроці ми систематизували наші теоретичні знання та практичні навички за темою «Рівняння, що зводяться до квадратних». Розглянули можливі шляхи розв’язку більш складних рівнянь. Переглянули та прослухали цікаві історичні доповіді, розширили свій світогляд.
VІІ. Релаксація
А зараз пропоную на декілька хвилин поринути у світ чудової природи нашої рідної Чернігівщини, переглянувши відеоролик, який створив мій одногрупник, випускник 1984 р. ЧДПІ ім. Т.Г. Шевченка, колишній вчитель математики, Тібеж С.Д. (Слайд 14).
VІІІ. Домашнє завдання (диференційоване)
На ваших аркушах із кросвордом записано три рівняння, виберіть будь-які два з них, що зможете розв’язати.
Математичний кросворд
|
|
|
|
1 Д |
И |
С |
К |
Р |
И |
М |
І |
Н |
А |
Н |
Т |
|
|
|
2 К |
О |
Р |
Е |
Н |
І |
|
|
|
|
|
|
|
|
|
|
|
3 Б |
І |
К |
В |
А |
Д |
Р |
А |
Т |
Н |
І |
|
|
|
|
4 С |
У |
М |
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 Т |
Е |
О |
Р |
Е |
М |
А |
|
|
|
|
|
|
6 Н |
Е |
П |
О |
В |
Н |
І |
|
|
|
|
|
|
|
|
|
7 З |
Н |
А |
К |
|
|
|
|
|
|
|
|
|
|
|
Домашнє завдання:
-
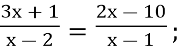 (4 б.)
(4 б.)
-
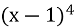 - 5
- 5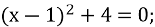 (5 б.)
(5 б.)
-
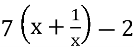 (
(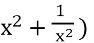 = 9. (6 б.)
= 9. (6 б.)
Бажаю всім успіхів!
Література
- Колесникова Л.В., Коротіна Г. Й.
Алгебра. Дидактичні матеріали: 8 клас: Навч. посібник. – Х.:
Світ дитинства, 2000. – 80 с.
- Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., Якір М. С.
МЗ – 41 Збірник задач і контрольних робіт з алгебри для 8 класу. –
Харків: Гімназія, 2008. – 96с.: іл.
Аркуші для учнів
Математичний кросворд
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Домашнє завдання
-
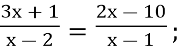 (4б)
(4б)
-
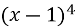 -5
-5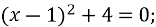 (5б)
(5б)
-
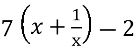 (
(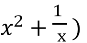 = 9; (6б)
= 9; (6б)


про публікацію авторської розробки
Додати розробку

