Додаток 3

Урок алгебри у 9 класі

Тема.  Геометрична прогресія. Розв’язування задач

Мета уроку:

освітня:  сформувати математичні компетенції: поглибити знання учнів про арифметичну і геометричну прогресії, навчити застосовувати знання про прогресії для розв’язування життєвих задач;

 розвиваюча: формувати практичну та логічну компетенції шляхом удосконалення вміння розв’язувати біологічні, фізичні задачі; розвивати уявлення про ідеї і методи математики та їх роль у пізнанні навколишнього світу, розв’язуванні  практичних задач; прищеплювати інтерес до математики;

виховна:  формувати соціальні, здоров’язберігаючі, комунікативні компетенції, виховувати уявлення про математику як невід’ємну складову загальнолюдської культури.

Обладнання:  комп’ютер, проектор, екран, мультимедійна презентація до уроку, відеоролики учнів «Геометрична прогресія в нашому житті», картки для індивідуальної самостійної роботи, кубик Блума.

Форми і методи роботи: ігрові методи, колективні форми роботи, випереджаючі завдання, інтерактивні вправи «знайди відповідність», «мікрофон», «кубування», індивідуальна самостійна робота учнів.

Тип уроку: застосування знань, умінь і навичок.

 

Хід уроку

І. Етап орієнтації, мотивації навчальної діяльності

Вчитель.  Добрий день. Сьогодні ми з вами проводимо ще один урок з теми «Геометрична прогресія». І цей урок незвичайний, бо на ньому ми дізнаємося багато нового.

ІІ. Етап цілепокладання

Вчитель.   Що ви чекаєте від сьогоднішнього уроку?  Відповідь на це запитання вам допоможе дати ось цей чарівний кубик, на гранях якого зображені запитання, з яких треба сформулювати нашу мету уроку.

Інтерактивна вправа  «Кубування» за допомогою кубика  Блума

Презентується кубик, на гранях якого зображено запитання: Як?Чому? Навіщо? Що? Коли? Де?

Вчитель. Так, на сьогоднішньому

уроці ми узагальнимо знання з цієї теми і знайдемо її застосування під час вивчення питань інших наук і життєвих ситуацій.

Оголошення теми і мети уроку.

Вчитель.  Внутрішня гармонія, строга витончена краса роблять теорію  прогресій відображенням  властивостей об’єктивного світу, що існує незалежно від нас, нашої свідомості. Адже,

Прогрес – це рух, це велич, це зростання,

Як Україні зараз він потрібний,

Прогресії – його сестриці рідні.

Це школа, математика, навчання.

І кожен з нас, як аксіому знає:

Без математики на ноги нам не стати

Тож хай лунає лозунг наш крилатий

Прогресу без прогресій не буває!

Переконатися в цьому нам допоможе виконане додаткове домашнє завдання. Тобто, для групи Б  було підготувати повідомлення  або відеоролик на тему «Геометрична прогресія у давнину і в сучасному житті». Давайте поглянемо і послухаємо.

Перегляд відеороликів «Геометрична прогресія у давнину і в сучасному житті»

ІІІ. Етап цілереалізації

1. Перевірка домашнього завдання

Вчитель. Однією із задач, яку  нам презентували дівчатка, була задача-легенда про винахідника шахмат, яка була вам додому.  Домашнє завдання заключалося в тому, щоб підрахувати сучасними  способами і

записати, скільки зерен повинен був отримати винахідник  шахмат?

(Учні оголошують результати домашніх розрахунків, а потім перевіряють за  слайдом)

S₆₄ = 2⁶⁴ – 1 = 18 446 744 073 709 551 615)

Вчитель. Хто зможе прочитати це число?

Отже, це число читається так: 18 квінтильйонів 446 квадрильйонів 744 трильйони 73 мільярди (більйони) 709 мільйонів 551 тисяча 615.

А сучасники сказали б так:  S₆₄ = 1, 84• 10¹⁹ – стандартний  вигляд  даного числа.

Вчитель.   Якщо  б   індуському царю Шерам вдалося засіяти пшеницею площу всієї поверхні Землі, враховуючи  і моря, і океани, і гори, і пустелі, і Арктику з Антарктикою, і отримати задовільний результат, то, напевно, років за 5 він зміг би розрахуватися.

2. Коригування опорних знань

Вчитель. Але не тільки  при розрахунках в економіці можна зустрітися з прогресіями. І сьогодні на уроці ми з вами розвʼяжемо ще кілька цікавих задач.

Але спочатку я пропоную вам пригадати основні поняття і формули прогресій.

Інтерактивна вправа «Знайди відповідність»

( На екрані записані формули та їх назви. Необхідно встановити відповідність між номером формули та її назвою. Формули і назви спроектовано на екран).

•       Ваше завдання: розташувати формули в тому порядку , в якому записані їх назви, тобто створити і записати число, яке у вас утвориться.

 

 

 

 

 

 

 

 

 

 

 

 

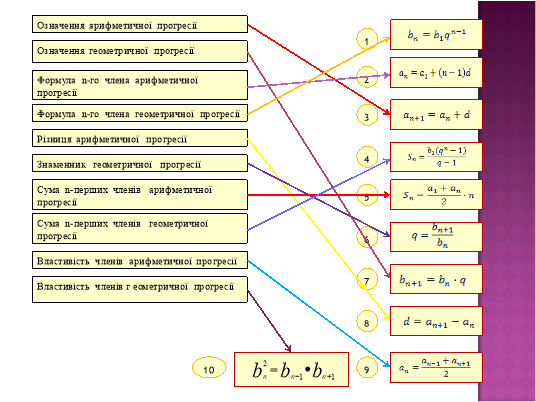
Питання:       

Означення арифметичної прогресії.

Означення геометричної прогресії.

Формула n-го члена арифметичної прогресії.

Формула n-го члена геометричної  прогресії.

Різниця  арифметичної  прогресії.

Знаменник геометричної прогресії.

Сума n-перших членів арифметичної  прогресії.

Сума n-перших членів геометричної прогресії.

Властивість членів арифметичної прогресії.

Властивість  членів геометричної  прогресії.

Учні записують код в зошиті.

КОД:   37  218  654  910 

Отже, ми повторили усі формули, а тепер застосуємо знання до розвʼязування задач

3. Розв’язування усних задач (задачі проектуються на екран)

Задача № 1. Яка із послідовностей є арифметичною прогресією, яка геометричною?

А) 1; 2; 4; 8   Б) 8; 10; 13; 17    В) 2; 4; 6; 8    Г) -8; 8; -8; 8. (а, г – геом. в – арифм.)

Задача № 2. Чому дорівнює третій член арифметичної прогресії, перший член якої дорівнює 5, а різниця  – 3?   (-1)

Задача № 3. Чому дорівнює сьомий член першої прогресії?    (64)

Задача № 4. Чому дорівнює 20 член останньої прогресії?  А 101-й?

 Вчитель. В біології прогресії пов’язані з такими темами, як розмноження, поділ клітин, форменні елементи крові та інші. Неможливо розв’язати біологічні задачі з даних тем, не використавши знання про прогресії. За теорією еволюції Дарвіна, всі процеси, які пов’язані з живими організмами, відбуваються прогресивно або регресивно.

На стадії ембріона відбувається процес формування тканин, який називається гістогенез. Одним з видів сполучної тканини, яка формується на стадії формування ембріона, є кров, до складу якої входять життєво необхідні клітини – еритроцити, лейкоцити та тромбоцити, кількість яких впливає на самопочуття людини.

Як впливає кількість еритроцитів на самопочуття людини?

Задача № 4.  (самостійно) Кількість еритроцитів ( з розрахунку на 1 мм³) в крові людини становить на рівні моря – 5 мільйонів. Через кожні 600 м підняття в гору їх кількість збільшується на 1 мільйон. Яка кількість еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест (4800 м) . Чому це відбувається? Застосуйте ваші знання з математики.

 

Вчитель. В чому математична суть і яка математична модель цієї задачі?  (Розв’язування задачі письмово. Учні після обговорення записують самостійно, а потім перевіряють)  

5,  6,  7,   8, …   Що це за послідовність?     

Що дано?    Що знайти?

a₁=5,  d = 1,  h = 4800,  h₁ = 600,  a_n - ?    

За якою формулою будемо обчислювати  a_n ?     

Чого не вистачає для обчислень за цією формулою? Як знайти п?

n = 4800 : 600 = 8,       

Обчисліть самостійно а₈.      

Перевірте: a₈ = a₁ + 1(n – 1) = 5 + 7 = 12 (млн)     

Відповідь: 12 млн

Вчитель. Чому це відбувається запитаємо у нашого гостя – Людмили Ростиславівни, учителя хімії та біології?

• У зв’язку з розрідженим повітрям в легені більше потрапляє кисню, відповідно цьому збільшується кількість еритроцитів.

Вчитель.  Процес розмноження відбувається прогресивно. Спробуємо розв’язати таку проблему:

Задача № 5 (письмово). Уявімо, що на початку нашої ери жінка М народила дві доньки, кожна з них до 30 років народила теж дві доньки і т.д. Чи можливо це? Скільки б за таких умов нащадків М жило б у наш час?

Вчитель.  Проаналізуємо цю задачу. В чому математична суть і яка математична модель цієї задачі?

На початку ери  2, через 30 років 4, через 40 років 8, …  Отже, утворився ряд чисел  1,  2,  4,  8,  16,  32, …  Що це за послідовність?   (Геометрична прогресія)   Що відомо?  b₁ = 1,   q = 2, час – 1000 років,   період – до 30 років,   S_n -?   

(Учні розв’язують цю задачу на дошці та в зошитах, а потім перевіряють)

n = 1000 : 30 34

.

.    

Відповідь:  73786976294838206464

Вчитель.   Чи можливо це? Це  число значно перевищує кількість людей на планеті. Тому це не можливо.

 

Вчитель.  На початку вивчення теми ми розглядали задачу, яку залишили без розв’язання, бо тоді нам не вистачило знань, щоб розв’язати її. 

А зараз ми повернемося до неї.  (Задача з підручника)   

Задача 832.  Бактерія, потрапивши в організм людини, до кінця 20-ї хвилини ділиться на 2, кожна з них через 20 хв ще на дві і т.д. Скільки бактерій стане в організмі людини через добу?

Що маємо? 1,  2, 4, 8, 16, … - геометрична прогресія,    

Що дано?  b₁ = 1,  q = 2,   час – 1 доба        

Що знайти?  S_n                                           

Розв’язання

хвилин у добі  60 х 24 = 1440 (хв.),   n = 1440 : 20 = 72,  

.  

Відповідь:  

Вчитель.  Можете уявити собі, що робиться в вашому організмі через добу! Ця задача закликає вас не нехтувати правилами власної гігієни.

А тепер, до вашої уваги – фізична задача, яку потрібно розвʼязати самостійно.

Задача №6 (письмово самостійно).    

Гальмуючи, автомобіль за першу секунду проїхав 15 м, а за кожну наступну – на 3 м    менше, ніж за попередню. Знайдіть гальмівний шлях автомобіля.

Що дано?         a₁ =15,   d = -3,   a_n = 0,   

Що знайти?      S_n - ?                                

Розв’язання.  Як знайти п?  Яку формулу використати?

                                        a_n = a₁ + d(n – 1),

                                        15 – 3(n -1) = 0,

                                         n  = 6,

            S₆ =  

Відповідь: 45 м. 

Вчитель. Отже, ця задача застерігає кожного з нас, що треба бути уважним на дорозі.

•                 Чи можемо ми тепер стверджувати, що прогресу без прогресій не буває? І чи  можна життя назвати прогресією?

 

ІV. Етап рефлексивно-оцінюючий

1.               Рефлексія

Вчитель.  Не тільки в біології ми можемо зустрітися з прогресіями. А й у машинобудуванні , фізиці та в повсякденному житті. Давайте поглянемо ще на одну роботу вашого однокласника.

Відеоролик «Геометрична прогресія навколо нас»

Учень.  Коли я готувався до сьогодніш-нього уроку, то взагалі був здивований, бо куди б я не я заходив у Інтернеті , скрізь натикався на геометричну прогресію. Виявилося, що без неї ніяк.

Ось послухайте декілька фраз з інформаційних джерел та переконайтеся в цьому самі (Додаток 2).

2. Підведення підсумків уроку

Вчитель: На сьогоднішньому уроці ви побачили, що розв’язуючи задачі з біології, фізики можна використати властивості і формули арифметичних  та геометричних  прогресій, що приведе, іноді, до єдиного вірного шляху розв’язування цих задач. Під час виконання домашнього завдання ви не лише вчилися розвʼязувати задачі, а й дізналися багато нового, навчилися створювати  свої відеоролики, працювати  в мережі Internet. Я надіюся, що отримані знання стануть вам в нагоді у майбутньому.

Вчитель:   І ось  наш урок  закінчується. Чи досягли ми мети, яку ставили перед собою на початку уроку? А це ми дізнаємося з вправи «Все в твоїх руках»,  коли дамо відповіді на запитання.

3. Оцінювання діяльності

учнів на уроці

 

V.  Етап повідомлення домашнього  завдання

1.  Повторити п. 20-24

2. Розвʼязати задачу 830.

3. Розвʼязати задачу із папірусу Рінда.

4. Скласти та розв’язати прикладну

задачу, в якій можна застосувати

прогресії.

 

 

 

Додаток 1

Додаткові індивідуальні завдання

Задача 1

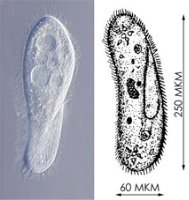
ІНФУЗОРІЇ. Влітку інфузорії розмножуються

безстатевим способом діленням навпіл.

 Питання: скільки буде інфузорій після

15-го розмноження?

 

Відповідь: b15 = 2•214 = 32 768 (геометрична прогресія).

__________________________________________________

 

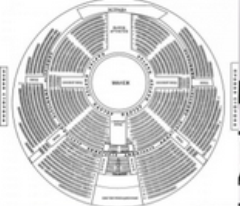Задача 2.

Для глядачів циркових вистав крісла в

одному із секторів розставлені так, що

кожен наступний ряд містить на одне

місце більше, ніж попередній. Скільки

місць установлено в секторі якщо в

першому ряду 8 крісел, а всього рядів 22?

 

Відповідь:  S₂₂ = 407 місць (арифметична прогресія)

__________________________________________________________

 

Задача 3.

Було це майже сто років тому. Селянин продавав

20 овець за 200крб. Коли один з покупців почав

надто довго торгуватись, селянин запропонував:

«Дай за першу вівцю 1к., за другу-2., за третю-4к.,

 і далі кожну вівцю вдвічі більше копійок, ніж за

попередню». Покупець погодився. Скільки він

заплатив за тих 20 овець?

 

Додаток 2

З інформаційних джерел

•       Кількість хворих на смертоносний вірус Ебола зростає у геометричній прогресії. Про це повідомили представники Всесвітньої організації охорони здоров'я.
•       Корупція зростає при зміні влади в геометричній прогресії.
•       У ніч з 25 на 26 квітня 1986 року на Чорнобильській атомній електростанції відбулася аварія, яка різко змінила мільйони людських доль. Радіоактивний викид на довгі роки відрізував від цивілізації десятки кілометрів поліської землі, які стали носити найменування, що шокує людську свідомість: "зона відчуження". Аварія обернулася катастрофою. По злих законах геометричної прогресії радіація понесла з цього життя спочатку працівників станції, які знаходилися на ній в ту зловісну ніч, потім - героїв-пожежників, що безстрашно боролися з радіоактивним вогнем на даху четвертого енергоблоку АЕС.
•       Парадокс сімейної геометричній прогресії. Поінформованість інших членів сім’ї про ваших тимчасових труднощах, збільшує ризик перевести їх в категорію постійних. Тому чим менше знають бабусі і дідусі, свекрухи, тещі, зовиці, дівера, сестри про те, що ти посварилася з чоловіком, тим більше шансів врятувати свій шлюб. Геометрична прогресія стосується і обізнаності подруг, колег, товаришів, сусідок про те, що діється в твоїй родині.
•       Наша здатність до інновацій зростає в геометричній прогресії, у міру того як йдуть роки. Щоб дати вам уявлення про значущість цієї прогресії, в інтернеті вам пропонують 10 інновацій, які повинні змінити наше життя до 2020 року.

–          Одна самка собаки в рік може принести до 16 цуценят ,за два роки це вже 128 нащадків ,а ще через рік 512 й так далі по геометричній прогресії. 

–  Між тим, з підвищенням рівня добробуту змінюється і наша манера споживання ресурсів. Обсяги споживання зростають в геометричній прогресії – більше ресурсів, більше енергії, щоб забезпечити вищий за наших попередників рівень життя!

–  Ініціативність, поряд з рішучістю, у ряді випадків цінуються вище правильної відповіді (дивно, але факт!). Зробивши звичним для себе таку поведінку, ви в геометричній прогресії нарощуєте власну сміливість і рішучість.

– Стосовно до людського суспільства Мальтус стверджував, що народонаселення зростає в геометричній прогресії (тобто як 1, 2, 4, 8, 16, 32, 64, 128, 256), тоді як засоби існування, на його думку, зростають у арифметичній прогресії (тобто як 1, 2, 3, 4, 5, 6, 7, 8, 9 ...).

•   Навіть, у словах пісні  «Ти подумай» гурту «Тартак» також є згадка про геометричну прогресію. Хто би міг подумати…

Ми живемо у колі вузьких інтересів –
Побутових умов, механічних процесів.
Сонце марно дарує нам позитивні фотони –
В нас крутіші мобільні, в нас модніші рінґтони!
Застрибнути на пік матеріального статку,
Від проблем заховатись, наче равлик у хатку.
Не почув, не побачив і сказати не може,
Це для нього чуже, а це на нього не схоже.
Телевізор, диван, пиво, футбол...
Тупий серіал, примітивний прикол...
Книга – просто додаток до шкільної програми,
А все, що потрібно, нам розкаже реклама!
Та кожен, хто вірить, почувається в силі
Так змінити життя, щоб радіти щохвилі!
Щоб ця радість росла в геометричній прогресії,
Щоб звільнити цей світ від журби та депресій!